3.5.6. Электромагнитная индукция
В 1831 г. английский физик Майкл Фарадей обнаружил на опыте, что в замкнутом проводнике при изменении потока магнитной индукции через поверхность, ограниченную контуром проводника, возникает электрический ток. Это явление называют электромагнитной индукцией. В опыте Фарадея проводник играет роль прибора, регистрирующего возникновение электродвижущей силы
ε = ∫ Edl , где L — контур, ограничивающий поверхность, кото-
L
рую пересекает изменяющийся магнитный поток. Закон электро-
магнитной индукции Фарадея связывает величину ЭДС ε с изменением магнитного потока
ε = − |
dΦ |
(3.111). |
|
dt |
|||
|
|
Магнитный поток может изменяться за счет изменения площади поверхности, пересекаемой линиями B, угла между нормалью к элементу поверхности и направлением B и самой величины B.
Важным проявлением электромагнитной индукции является самоиндукция проводников. Всякий контур, по которому протекает электрический ток, создает магнитный поток через поверхность, ограниченную этим контуром. При изменении магнитного потока в контуре возникает разность потенциалов, называемая ЭДС самоиндукции.
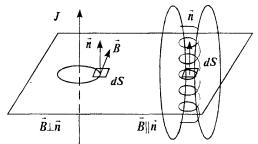
Магнитный поток, создаваемый проводником, зависит не только от силы протекающего тока, но и от формы проводника. На рис. изображены поля, создаваемые одним и тем же проводником, но в первом случае контур проводника имеет форму линейного прово-
19
да, а во втором — катушки соленоида. Для линейного проводника создаваемый им магнитный поток на единицу поверхности горизонтальной плоскости равен нулю (B n) , для соленоида
ddSΦ = B (В n).
Способность проводящего контура создавать магнитный поток при протекании по нему электрического тока называют индуктивностью
Ф = LI, |
(3.112) |
где Ф — полный магнитный поток, создаваемый контуром. Например, полный магнитный поток, создаваемый соленоидом
длины , имеющим N витков, |
|
Ф = N ф = N B S = μ0 n2 S I |
(3.113) |
(здесь ф — магнитный поток, создаваемый одним витком тока). Сравнивая с (3.116), для индуктивности соленоида находим:
L = μ0 n2 S = μ0 n2 V, |
(3.114) |
где V— объем соленоида. Таким образом, индуктивность соленоида определяется его геометрическими характеристиками— объемом и плотностью витков.
Индуктивность в магнитостатике играет такую же роль, как емкость в электростатике. За единицу индуктивности принимают индуктивность такого проводника, который при пропускании по нему тока в 1 А создает единицу магнитного потока.
Подставляя выражение (3.116) в (3.115), для ЭДС самоиндукции получим:
εs = −L dI |
(3.115) |
dt |
|
3.5.7. Энергия магнитного поля
В электростатике, вычисляя энергию электрического поля в объеме, где сосредоточены заряды, мы видели, что энергия поля может быть выражена как в терминах создающего его заряда, так и непосредственно напряженности поля или разности потенциалов, существующих в этом объеме.
20
Аналогичным образом энергию магнитного поля можно выразить через величину тока, создающего это поле, либо через величину магнитной индукции.
Рассмотрим магнитостатическую систему — совокупность электрических проводников, по которым протекают постоянные токи. Эти токи взаимодействуют между собой посредством магнитного поля, что проявляется в существовании сил Ампера. Такая система токов вполне аналогична электростатической системе зарядов, рассмотренных в разделе 3.2.3. Напомним в связи с этим, что роль элементарного «магнитного заряда» выполняет
величина бесконечно малого потока заряда (см. 3.3.2.) dIQ = Id .
Энергия системы токов заключена в энергии их взаимодействия между собой. Эта энергия взаимодействия возникает как результат совершения работы над токами внешними силами против магнитного поля токов при создании магнитостатической системы. Для создания самого магнитного поля тока никакой дополнительной работы производить не нужно — магнитное поле существует вместе с постоянным током точно так же, как электрическое поле существует вместе с покоящимся зарядом.
При перемещении токов под действием сил Ампера, наоборот, магнитное поле совершает работу над токами. Мы вычислили эту работу в разделе 3.35:
dA = I dΦ,
где dΦ — изменение магнитного потока при перемещении тока. Используя соотношение (3.116), находим
dA = I dI,
откуда полная работа:
A = |
L I 2 |
. |
(3.116) |
|
2 |
||||
|
|
|
Таким образом, энергия магнитного поля, создаваемого в пространстве проводником, по которому протекает ток I,
W = |
L I 2 |
. |
(3.117) |
|
2 |
||||
|
|
|
Выразим эту энергию через величину магнитной индукции.
21