
- •3.5. Магнитостатика
- •3.5.1. Природа магнитного поля
- •3.5.2. Свойства магнитного поля. Закон Био-Савара
- •3.5.3. Силы в магнитном поле
- •А. Сила Лоренца
- •Б. Сила Ампера
- •В. Силы, действующие на замкнутый контур с током в однородном магнитном поле. Магнитный момент тока
- •3.5.4. Магнитное поле в веществе. Магнетики
- •3.5.5. Магнитный поток. Теорема Гаусса для магнитного поля. Поле соленоида
- •3.5.6. Электромагнитная индукция
- •3.5.7. Энергия магнитного поля
- •3.6. Уравнения Максвелла для электромагнитного поля.
- •3.6.1. Ток смещения. Возникновение магнитного поля при изменении электрического поля
- •3.6.2. Уравнения Максвелла.
- •IV. Колебания и волны
- •4.1. Механические колебания
- •4.1.1. Гармонические колебания. Осциллятор
- •4.1.2. Сложение колебаний
- •4.2. Электрические колебания
- •4.2.1. Свободные колебания в электрическом контуре
- •4.2.2. Вынужденные колебания. Резонанс
- •4.2.3. Переменный электрический ток
- •4.3. Волновое движение
- •4.3.1. Связанные гармонические осцилляторы. Упругие волны
- •4.3.2. Свойства бегущих волн
- •4.3.3. Энергия, переносимая волной. Стоячие волны
- •4.4. Генерация электромагнитных волн
- •4.4.1. Электромагнитные волны и уравнения Максвелла. Скорость распространения электромагнитных волн
- •4.4.2. Свет как электромагнитная волна. Шкала электромагнитных волн
- •4.4.3. Энергия электромагнитной волны.
- •4.4.4. Импульс электромагнитного поля
- •4.4.6. Заключение
- •Контрольная работа 4.
- •4.5. Равновесное электромагнитное излучение
- •4.5.1. Абсолютно черное тело
- •4.5.2. Классическое рассмотрение излучения черного тела. Ультрафиолетовая катастрофа
- •Глава 5.ОПТИКА.
- •5.1. Геометрическая оптика
- •5.1.1. Принцип Ферма
- •5.2. Волновая оптика
- •5.2.1. Опыт Юнга. Интерференция волн. Принцип Гюйгенса.
- •5.2.2. Метод графического сложения амплитуд. Дифракция от простейших преград.
- •5.2.3. Дифракционная решетка. Дифракция рентгеновских лучей
- •5.3. Физическая оптика
- •5.3.1. Поляризация света
- •5.3.2. Дисперсия света
- •Глава 6. ФОТОНЫ.
- •6.1. Коротковолновая граница рентгеновского спектра
- •6.2. Внешний фотоэффект
- •6.3. Эффект Комптона
- •Контрольная работа №5
- •7.1. Строение атома
- •7.1.1 Планетарная модель
- •7.1.2. Атомные спектры
- •7.1.3 Постулаты Бора
- •7.1.4. Упругие и неупругие столкновения
- •7.1.5. Опыты Франка и Герца
- •7.2. Волновые свойства микрочастиц
- •7.2.1. Гипотеза де Бройля
- •7.2.2. Свойства микрочастиц
- •7.2.3. Соотношение неопределенностей
- •7.2.4. Волна де Бройля.
- •7.3. Уравнение Шредингера.
- •7.3.1. Волновые функции
- •7.3.2. Уравнение Шрёдингера
- •7.3.3 Прохождение частиц через потенциальный барьер
- •7.3.4. Квантование энергии
- •7.3.5. Собственные значения физических величин
- •7.3.6. Квантование момента импульса
- •7.3.7. Гармонический осциллятор
- •7.3.8. Атом водорода
- •Глава 8. АТОМНОЕ ЯДРО
- •8.1. Ядерные силы
- •8.2. Некоторые свойства ядер
- •8.3. Энергия связи ядра
- •8.4. Радиоактивность
- •8.5. Постоянная распада
- •8.6. Период полураспада
- •8.7. Кривая роста дочерних ядер
- •8.8. Радиоактивные семейства ядер
- •8.9. Датировка событий методом радиоактивных распадов
- •Контрольная работа №6
квантовое, не имеющее аналога в классической физике. В квантовой же механике деление полной энергии на кинетическую и потенциальную не имеет смысла, так как противоречит принципу неопределенности. Действительно, тот факт, что частица обладает определенной кинетической энергией Ek, был бы равнозначен тому, что частица имеет определенный импульс p. Аналогично тот факт, что частица имеет определенную потенциальную энергию U, означал бы, что частица находится в точно заданном месте пространства. Поскольку координата и импульс частицы не могут одновременно иметь определенных значений, не могут быть одновременно точно определены Ek и U. Таким образом, хотя полная энергия частицы E имеет вполне определенное значение, она не может быть представлена в виде суммы точно определенных энергий Ek и U. Ясно, что в этом случае заключение об отрицательности Ek «внутри» туннеля становится беспочвенным.
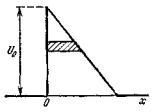
Туннельный эффект позволяет объяснить ряд явлений, в частности вырывание электронов из металлов электрическим полем (автоэлектронную эмиссию). Если создать вблизи металла сильное электрическое поле, то ступенчатый барьер, удерживающий свобод-
ные электроны в металле, превращается в барьер конечной ширины Созданное вблизи поверхности металла очень сильное электрическое поле превращает ступенчатый потенциальный барьер в барьер конечной ширины. Вне металла потенциальная энергия электрона равна U0 — eφ = U0 — eEx (φ — потенциал, E — модуль напряженности поля).
В результате становится возможным выход электронов из металла за счет туннельного эффекта. Чем сильнее поле, тем уже барьер и тем больше коэффициент прохождения D.
7.3.4. Квантование энергии
Уравнение Шрёдингера позволяет найти волновую функцию данного состояния и, следовательно, определить вероятность на-
189
хождения частицы в различных точках пространства. Однако этим далеко не исчерпывается значение указанного уравнения. Из уравнения (7.23) и налагаемых на волновые функции стандартных условий непосредственно вытекает квантование энергии частицы.
Вуравнение Шрёдингера входит в качестве параметра полная энергия частицы E. В теории дифференциальных уравнений доказывается, что уравнения вида (7.23) имеют решения, удовлетворяющие стандартным условиям, не при любых значениях параметра (т. е. энергии E), а лишь при некоторых избранных значениях. Эти избранные значения называются собственными значениями соответствующей величины (в нашем случае—-энергии). Решения, соответствующие собственным значениям E, называются собственными функциями задачи.
Совокупность собственных значений называется спектром величины. Если эта совокупность образует дискретную последовательность, спектр называется дискретным. Если собственные значения образуют непрерывную последовательность, спектр называют непрерывным или сплошным. В дальнейшем мы ограничимся рассмотрением только таких задач, у которых спектр собственных значений является дискретным.
Вслучае дискретного спектра собственные значения и собственные функции можно пронумеровать:
E1, E2, ...., En, ....., |
|
ψ1, ψ2, , ψn, .... |
(7.31) |
Таким образом, квантование энергии получается из основных
положений квантовой механики без каких-либо дополнительных предположений.
Нахождение собственных значений и собственных функций, как правило, представляет весьма трудную математическую задачу. Мы рассмотрим пример, достаточно простой для того, чтобы можно было решить уравнение Шрёдингера без большого труда.
Найдем собственные значения энергии и соответствующие им собственные функции для частицы, находящейся в бесконечно глубокой одномерной потенциальной яме. Предположим, что частица может двигаться только вдоль оси x. Пусть движение ограничено непроницаемыми для частицы стенками: x = 0 и x = 1.
190
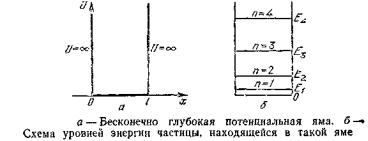
Потенциальная энергия U имеет в этом случае следующий вид (рис. а): она равна нулю при 0 ≤ х ≤ и обращается в бесконеч-
ность при x < 0 и х > 1.
Возьмем уравнение Шрёдингера в виде (7.27). Поскольку волновая функция зависит только от координаты х, уравнение упрощается следующим образом:
d 2ψ |
+ |
2m (E −U )ψ = 0 . |
(7.32) |
dx2 |
|
2 |
|
За пределы потенциальной ямы частица попасть не может. Поэтому вероятность обнаружения частицы вне ямы равна нулю. Соответственно и функция ψ за пределами ямы равна нулю. Из условия непрерывности следует, что ψ должна быть равна нулю и на границах ямы, т. е. что
ψ(0) = ψ( ) = 0. |
(7.33) |
Это и есть то условие, которому должны удовлетворять решения уравнения (7.24).
В области, где ψ не равна тождественно нулю, уравнение (7.24) имеет вид
d 2ψ |
+ |
2m Eψ = 0 |
(7.34) |
dx2 |
|
2 |
|
(в этой области U = 0). Введя обозначение
k2 = |
2m |
E |
(7.35) |
|
|||
|
2 |
|
|
191
придем к уравнению, хорошо известному из теории колебаний: ψ" + k2ψ = 0.
Решение такого уравнения имеет вид
ψ(х) = A∙sin (kx + α). (7.36)
Условиям (7.33) можно удовлетворить соответствующим выбором постоянных k и α. Прежде всего из условия ψ(0) =0 получаем,
ψ(0) = Asinα = 0,
откуда следует, что α должна быть равна нулю. Далее, должно выполняться условие
ψ( ) = Asin(k ) = 0, |
|
что возможно лишь в случае, если |
|
k =±nπ (n=1, 2, 3, ...) |
(7.37) |
(n = 0 отпадает, поскольку при этом получается ψ =0 — частица нигде не находится).
Исключив k из уравнений (7.35) и (7.37), найдем собственные значения энергии частицы:
E |
= |
π2 2 |
n2 |
(n = 1, 2, 3,...). |
(7.38) |
n |
|
2m 2 |
|
|
|
Спектр энергии оказался дискретным. На рис.б изображена схема энергетических уровней.
Оценим расстояния между соседними уровнями для различных значений массы частицы m и ширины ямы . Разность энергий двух соседних уровней равна
∆E |
= E |
− E |
= π2 2 |
(2n +1)≈ π2 2 n . |
(7.39) |
|
n |
|
n+1 |
n |
2m 2 |
m 2 |
|
Если взять m порядка массы молекулы (~ 10-26 кг), а порядка |
||||||
0,1 м (размеры сосуда, в котором находится газ), получится |
|
|||||
∆E |
= |
3,142 1,052 10−68 |
|
|||
10−26 |
0,12 |
n =10-39n Дж ~ 10-20n эВ. |
||||
n |
|
|
|
|||
Столь густо расположенные энергетические уровни будут практически восприниматься как сплошной спектр энергии, так что хотя квантование энергии в принципе будет иметь место, но на
192

характере движения молекул сказываться не будет. Аналогичный результат получается, если взять m порядка мас-
сы электрона (~ 10-30 кг) при тех же размерах ямы (свободные
электроны в металле). В этом случае
En~10-35n Дж ~ 10-16n эВ.
Однако совсем иной результат получается для электрона, если область, в пределах которой он движется, будет порядка атомных размеров (~ 10-10 м). В этом случае подстановка в формулу (7.35)
числовых значений дает
En~10-17n Дж ~ 102n эВ.
Согласно формуле (7.34) минимальная энергия, которой может обладать частица, находящаяся в потенциальной яме, отлична от нуля. Этот результат обусловлен волновыми свойствами частицы и может быть получен из соотношения неопределенностей. Неопределенность координаты x в этом случае ограничена размером
сосуда . Поскольку |
x = , неопределенность импульса p (т. е. в |
данном случае сам импульс p) равна
p = p ≥ ħ/Δx = ħ/ .
Следовательно, энергия частицы ограничена снизу значением
Emin ≈ p2 ≈ 2 ,
2m m 2
которое с точностью до множителя π2 совпадает с выражением
(7.34) для n=1.
Подставив в (7.32) значение k, получающееся из условия (7,33), найдем собственные функции задачи:
ψ (x)= Asin nπx
(напомним, что α = 0). Для нахождения коэффициента A воспользуемся условием нормировки
∫Ψ*ΨdV = A2 ∫sin2 nπx dx =1.
193
На концах промежутка интегрирования подынтегральная функция обращается в нуль. Поэтому значение интеграла можно полу-
чить, умножив среднее значение sin2(nπx/ ) (равное, как известно, 1/2) на длину промежутка . В результате получится: A2(1/2) = 1,
откуда A = 
 2
2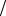 . Таким образом, собственные функции имеют вид
. Таким образом, собственные функции имеют вид
ψn (x)= |
2 |
sin |
nπx |
(n=1, 2, 3, ...). (7.40) |
|
|
|
||||
|
|
|
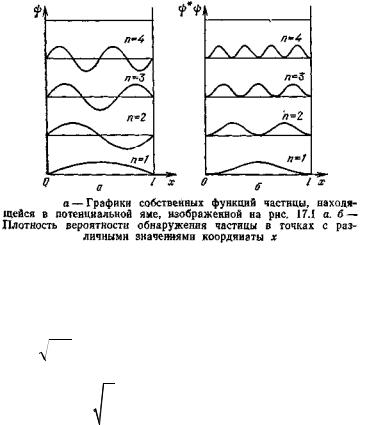
Графики собственных функций изображены на рис.а. На рис.б дана плотность вероятности обнаружения частицы на различных расстояниях от стенок ямы, равная ψ*ψ. Из графиков, например, следует, что в состоянии с n = 2 частица не может быть обнаружена в середине ямы и вместе с тем одинаково часто бывает как в левой, так и в правой половине ямы. Такое поведение частицы, очевидно, несовместимо с представлением о траекториях. Отметим, что согласно классическим представлениям все положения частицы в яме равновероятны.
194
