очень малых размеров (макроскопическая частица), не может служить прообразом микрочастицы. С уменьшением размеров начинают проявляться качественно новые свойства, не обнаруживающиеся у макрочастиц.
В ряде случаев утверждение об отсутствии траекторий у микрочастиц, казалось бы, противоречит опытным фактам. Так, например, в камере Вильсона путь, по которому движется микрочастица, обнаруживается в виде узких следов (треков), образованных капельками тумана; движение электронов в электронно-лучевой трубке превосходно рассчитывается по классическим законам, и т. п. Это кажущееся противоречие объясняется тем, что при известных условиях понятие траектории оказывается применимым к микрочастицам, но только с некоторой степенью точности. Положение оказывается точно таким, как в оптике. Если размеры преград или отверстий велики по сравнению с длиной волны, распространение света происходит как бы вдоль определенных лучей (траекторий). При определенных условиях понятие траектории оказывается приближенно применимым к движению микрочастиц, подобно тому как оказывается справедливым закон прямолинейного распространения света.
7.2.3. Соотношение неопределенностей
В классической механике состояние материальной точки (классической частицы) определяется заданием значений координат, импульса, энергии и т. д. Перечисленные величины называются динамическими переменными. Строго говоря, микрообъекту не могут быть приписаны указанные динамические переменные, однако информацию о микрочастицах мы получаем, наблюдая их взаимодействие с приборами, представляющими собой макроскопические тела. Поэтому результаты измерений поневоле выражаются в терминах, разработанных для характеристики макротел, т. е. через значения динамических переменных. В соответствии с этим измеренные значения динамических переменных приписываются микрочастицам. Например, говорят о состоянии электрона, в котором он имеет такое-то значение энергии, и т. д.
Своеобразие свойств микрочастиц проявляется в том, что не
175
для всех переменных получаются при измерениях определенные значения. Так, например, электрон (и любая другая микрочастица) не может иметь одновременно точных значений координаты х и компоненты импульса рх. Неопределенности значений x и px удовлетворяют соотношению
∆x ∆px ≥ћ/2 |
(7.15) |
(ћ—постоянная Планка). Из (7.15) следует, что чем меньше неопределенность одной из переменных (х или рх), тем больше неопределенность другой. Возможно такое состояние, в котором одна из переменных имеет точное значение, другая переменная при этом оказывается совершенно неопределенной (ее неопределенность равна бесконечности).
Соотношение, аналогичное (7.15), имеет место для у и ру, для z и рz, а также для ряда других пар величин (в классической механике такие пары величин называются канонически сопряженными). Обозначив канонически сопряженные величины буквами А и В, можно написать
∆A ∆B ≥ ћ/2. |
(7.16) |
Эта формула называется соотношением неопределенностей для величин А и В. Его открыл В. Гейзенберг в 1927 г.
Утверждение о том, что произведение неопределенностей значений двух сопряженных переменных не может быть по порядку величины, меньше постоянной Планка ћ, называется принципом неопределенности Гейзенберга.
Энергия и время являются канонически сопряженными величинами. Поэтому для них также справедливо соотношение неопреде-
ленностей: |
|
∆E ∆t ≥ ћ/2. |
(7.17) |
Это соотношение означает, что определение энергии с точностью ∆E должно занять интервал времени, равный по меньшей мере ∆t ~ ћ/∆E.
Соотношение неопределенностей было установлено из рассмотрения, в частности, следующего примера. Попытаемся определить значение координаты х свободно летящей микрочастицы,
поставив на ее пути щель ширины ∆x:, расположенную перпендикулярно к направлению движения частицы (рис.).
176
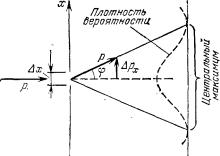
Дифракция частицы на щели. Уменьшение неопределенности координаты x; от ∞ до ∆x: сопровождается возрастанием неопределенности
компоненты импульса pх от нуля до ∆px
До прохождения частицы через щель ее компонента импульса рх имеет точное значение, равное нулю (щель по условию перпен-
дикулярна к импульсу), так что ∆px = 0, зато координата х частицы является совершенно неопределенной. В момент прохождения частицы через щель положение меняется. Вместо полной неопре-
деленности координаты х появляется неопределенность ∆x, но это достигается ценой утраты определенности значения рx. Действительно, вследствие дифракции имеется некоторая вероятность того, что частица будет двигаться в пределах угла 2ϕ, где ϕ – угол, соответствующий первому дифракционному минимуму (максимумами высших порядков можно пренебречь, поскольку их интенсивность мала по сравнению с интенсивностью центрального максимума). Таким образом, появляется неопределенность
∆px = p sinϕ.
Краю центрального дифракционного максимума (первому минимуму), получающемуся от щели ширины ∆x, соответствует угол ϕ, для которого
sinϕ = λ/∆x.
Следовательно,
∆px = pλ/∆x.
Отсюда с учетом λ = 2πћ/p получается соотношение
∆x ∆px = pλ = 2πћ,
согласующееся (по порядку величины) с (7.4).
177
Иногда соотношение неопределенностей получает следующее толкование: в действительности у микрочастицы имеются точные значения координат и импульсов, однако ощутимое для такой частицы воздействие измерительного прибора не позволяет точно определить эти значения. Такое толкование является совершенно неправильным. Оно противоречит наблюдаемым на опыте явлениям дифракции микрочастиц.
Соотношение неопределенностей обусловлено корпускулярноволновой природой микрообъектов. Оно указывает, в какой мере можно пользоваться понятиями классической механики применительно к микрочастицам, в частности, с какой степенью точности можно говорить о траекториях микрочастиц. Движение по траектории характеризуется вполне определенными значениями коор-
динат и скорости в каждый момент времени. Подставив в ∆x ∆px ≥ћ/2 вместо рх произведение тvх, получим соотношение
∆x ∆v ≥ /2m.
Мы видим, что чем больше масса частицы, тем меньше неопределенности ее координаты и скорости и, следовательно, с тем большей точностью применимо понятие траектории. Уже для макрочастицы размером всего 1 мкм неопределенности значений х и vx оказываются за пределами точности измерения этих величин, так что практически ее движение будет неотличимо от движения по траектории.
7.2.4. Волна де Бройля.
Де Бройль связал со свободно движущейся частицей плоскую волну, смысл которой вначале оставался неясным. Реальная плоская волна, распространяющаяся в направлении оси х, описывается уравнением
ε = Acos(ωt – kx) = Acos(ωt – 2πx/λ).
Заменив в соответствии с формулами λ = 2πћ/p и ω = E/ћ ω и λ через E и p, уравнение волны де Бройля для свободной частицы пишут в виде
Ψ = Aexp[(i/ћ)(px–Et) |
(7.18) |
Функцию Ψ называют волновой функцией (или пси-функцией).
178
Она описывает состояние .частицы. Функция Ψ, как правило, бывает комплексной и в ряде случаев (когда частица движется в силовом поле) имеет не свойственный волне непериодический характер. Несмотря на это, ее и в этих случаях называют волновой.
Правильную интерпретацию волновой функции дал в 1926 г. Борн. Согласно Борну квадрат модуля волновой функции определяет вероятность dP того, что частица будет обнаружена в пределах объема dV;
dP = |Ψ|2 dV |
(7.19) |
Интеграл от выражения (7.8), взятый по всему пространству,
должен равняться единице: |
|
∫Ψ*ΨdV = 1. |
(7.20) |
Действительно, этот интеграл дает вероятность того, что частица находится в одной из точек пространства, т. е. вероятность достоверного события, которая равна единице.
Соотношение (7.20) носит название условия нормировки. Функции, удовлетворяющие этому условию, называются нормированными.
Из формулы (7.19) вытекает, что квадрат модуля волновой функции дает плотность вероятности (вероятность, отнесенную к единице объема) нахождения частицы в соответствующем месте пространства.
В соответствии со своим смыслом волновая функция должна быть однозначной, непрерывной и конечной (за исключением, быть может, особых точек). Кроме того, она должна иметь непрерывную и конечную производную. Совокупность перечисленных требований носит название стандартных условий.
Из физического смысла волновой функции вытекает, что квантовая механика имеет статистический характер. Она не позволяет определить местонахождение частицы в пространстве или траекторию, по которой движется частица. С помощью волновой функции можно лишь предсказать, с какой вероятностью частица может быть обнаружена в различных точках пространства. На первый взгляд может показаться, что квантовая механика дает значительно менее точное и исчерпывающее описание движения частицы, чем классическая механика, которая определяет «точно» ме-
179