
- •3.5. Магнитостатика
- •3.5.1. Природа магнитного поля
- •3.5.2. Свойства магнитного поля. Закон Био-Савара
- •3.5.3. Силы в магнитном поле
- •А. Сила Лоренца
- •Б. Сила Ампера
- •В. Силы, действующие на замкнутый контур с током в однородном магнитном поле. Магнитный момент тока
- •3.5.4. Магнитное поле в веществе. Магнетики
- •3.5.5. Магнитный поток. Теорема Гаусса для магнитного поля. Поле соленоида
- •3.5.6. Электромагнитная индукция
- •3.5.7. Энергия магнитного поля
- •3.6. Уравнения Максвелла для электромагнитного поля.
- •3.6.1. Ток смещения. Возникновение магнитного поля при изменении электрического поля
- •3.6.2. Уравнения Максвелла.
- •IV. Колебания и волны
- •4.1. Механические колебания
- •4.1.1. Гармонические колебания. Осциллятор
- •4.1.2. Сложение колебаний
- •4.2. Электрические колебания
- •4.2.1. Свободные колебания в электрическом контуре
- •4.2.2. Вынужденные колебания. Резонанс
- •4.2.3. Переменный электрический ток
- •4.3. Волновое движение
- •4.3.1. Связанные гармонические осцилляторы. Упругие волны
- •4.3.2. Свойства бегущих волн
- •4.3.3. Энергия, переносимая волной. Стоячие волны
- •4.4. Генерация электромагнитных волн
- •4.4.1. Электромагнитные волны и уравнения Максвелла. Скорость распространения электромагнитных волн
- •4.4.2. Свет как электромагнитная волна. Шкала электромагнитных волн
- •4.4.3. Энергия электромагнитной волны.
- •4.4.4. Импульс электромагнитного поля
- •4.4.6. Заключение
- •Контрольная работа 4.
- •4.5. Равновесное электромагнитное излучение
- •4.5.1. Абсолютно черное тело
- •4.5.2. Классическое рассмотрение излучения черного тела. Ультрафиолетовая катастрофа
- •Глава 5.ОПТИКА.
- •5.1. Геометрическая оптика
- •5.1.1. Принцип Ферма
- •5.2. Волновая оптика
- •5.2.1. Опыт Юнга. Интерференция волн. Принцип Гюйгенса.
- •5.2.2. Метод графического сложения амплитуд. Дифракция от простейших преград.
- •5.2.3. Дифракционная решетка. Дифракция рентгеновских лучей
- •5.3. Физическая оптика
- •5.3.1. Поляризация света
- •5.3.2. Дисперсия света
- •Глава 6. ФОТОНЫ.
- •6.1. Коротковолновая граница рентгеновского спектра
- •6.2. Внешний фотоэффект
- •6.3. Эффект Комптона
- •Контрольная работа №5
- •7.1. Строение атома
- •7.1.1 Планетарная модель
- •7.1.2. Атомные спектры
- •7.1.3 Постулаты Бора
- •7.1.4. Упругие и неупругие столкновения
- •7.1.5. Опыты Франка и Герца
- •7.2. Волновые свойства микрочастиц
- •7.2.1. Гипотеза де Бройля
- •7.2.2. Свойства микрочастиц
- •7.2.3. Соотношение неопределенностей
- •7.2.4. Волна де Бройля.
- •7.3. Уравнение Шредингера.
- •7.3.1. Волновые функции
- •7.3.2. Уравнение Шрёдингера
- •7.3.3 Прохождение частиц через потенциальный барьер
- •7.3.4. Квантование энергии
- •7.3.5. Собственные значения физических величин
- •7.3.6. Квантование момента импульса
- •7.3.7. Гармонический осциллятор
- •7.3.8. Атом водорода
- •Глава 8. АТОМНОЕ ЯДРО
- •8.1. Ядерные силы
- •8.2. Некоторые свойства ядер
- •8.3. Энергия связи ядра
- •8.4. Радиоактивность
- •8.5. Постоянная распада
- •8.6. Период полураспада
- •8.7. Кривая роста дочерних ядер
- •8.8. Радиоактивные семейства ядер
- •8.9. Датировка событий методом радиоактивных распадов
- •Контрольная работа №6
Описанную картину колебаний во встречных бегущих волнах называют стоячей волной. Ясно, что в замкнутом объеме, где бегущая волна испытывает отражение от обеих границ, устанавливается стоячая волна.
4.4. Генерация электромагнитных волн
Согласно Максвеллу, изменяющееся электрическое поле порождает в пустом пространстве магнитное поле. На этом основании Максвелл пришел к следующему заключению. Если изменяющееся магнитное поле приводит к появлению электрическою поля, то электрическое поле также будет изменяться. Это изменение электрического поля приведет в свою очередь к появлению изменяющегося магнитного поля и т.д. Анализируя свои уравнения, Максвелл обнаружил, что конечным итогом подобной связи изменяющихся полей будет появление волны, которая содержит электрическое и магнитное поля и способна распространяться в пустом пространстве! Попытаемся качественно разобраться в том. как возникает подобная электромагнитная волна (количественный анализ будет проведен в следующем разделе).
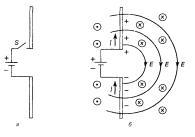 Рис.1 Рассмотрим «антенну» из двух проводящих стержней (рис.1а).
Рис.1 Рассмотрим «антенну» из двух проводящих стержней (рис.1а).
Допустим, что стержни через ключ соединены с клеммами батареи. При замыкании ключа верхний стержень быстро приобретает положительный заряд, а нижний отрицательный. Силовые линии электрического поля показаны на рис.2б. Пока заряды перемещаются к стержням, в антенне течет электрический ток I (стрелка указывает направление тока положительных зарядов). Электрический ток создает магнитное поле: силовые линии индукции маг-
53
нитного поля представляют собой окружности, охватывающие стержни антенны; на рисунке вектор индукции В направлен к
плоскости страницы справа от стержней Å и от плоскости страни-
цы слева О. Насколько далеко эти поля распространяются в пространстве? В статическом случае они уходили бы в бесконечность. Однако при замыкании ключа эти поля быстро возникают вблизи стержней, но для того, чтобы достичь удаленных точек, потребуется время: и электрическое, и магнитное поля обладают энергией, а энергия не может переноситься с бесконечно большой скоростью.
Этот пример служит иллюстрацией того, что электрическому и магнитному полям, чтобы достигнуть удаленных точек, требуется время. Представим себе теперь более интересную ситуацию.
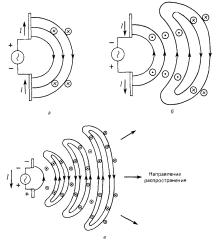 Рис.2 Предположим, что антенна подключена к генератору перемен-
Рис.2 Предположим, что антенна подключена к генератору перемен-
ного тока (рис. 2). (В этом случае она называется электрическим дипольным вибратором: в любой момент времени в антенне существует разделение положительных и отрицательных зарядов, и ее дипольный момент осциллирует.) На рис.2а антенна только что подключена к генератору; на стержнях стал накапливаться заряд, и картины полей выглядят, как на предыдущем рисунке. Знаки + и - соответствуют полярности зарядов на стержнях. Стрелки указы-
54
вают направление тока. Электрическое поле изображено силовыми линиями в плоскости рисунка, а магнитное поле, согласно правилу
правой руки, направлено к плоскости страницы (Å) или от нее (О).
На рис.2б ЭДС генератора проходит через максимум и начинает убывать, ток в антенне течет в противоположном направлении, и его магнитное поле направлено в противоположную сторону. Однако существовавшие до этого поля внезапно не исчезают: они распространяются в пространстве. Поскольку направление вновь возникших полей противоположно прежнему, силовые линии полей «замыкаются» и образуют замкнутые контуры. Спустя некоторое время эта картина силовых линий принимает вид, показанный на рис.2в (обратите внимание на изменение масштаба). Силовые линии полей продолжают распространяться от вибратора. Магнитные силовые линии также замкнуты, но на рисунке этого не видно, так как они расположены перпендикулярно плоскости рисунка.
Поля продолжают распространяться в пространстве, удаляясь от антенны. (Они распространяются во все стороны, а не только вправо, как показано на рис.) Напряженность электрического поля и индукция магнитного поля максимальны в направлениях, перпендикулярных направлению колебаний заряда в вибраторе; вдоль направления колебаний заряда - над и под антенной - поля обращаются в нуль.
Из рис. можно сделать несколько выводов. Во-первых, в любой
точке векторы E и B взаимно перпендикулярны и перпендикулярны направлению распространения. Во-вторых, поля изменяют
свое направление в пространстве: в одних точках вектор B направлен к плоскости страницы, в других - от нее; аналогично ведет
себя и вектор E . Напряженность электрического поля (и индукция магнитного поля) изменяется от максимума в одном направлении до нуля и возрастает до максимума в другом направлении. Электрическое и магнитное поля находятся в фазе, т. е они достигают максимума и обращаются в нуль в одних и тех же точках.
Если ЭДС генератора изменяется по синусоидальному закону, то и напряженность электрического поля, и индукция магнитного
55
поля будут изменяться по синусоидальному закону. Строго говоря, это справедливо в точках, достаточно удаленных от источника; вблизи антенны (в так называемом ближнем поле) картина полей оказывается довольно сложной. Нас интересуют поля на достаточном удалении от антенны (поля излучения); именно этой ситуации и соответствует картина, изображенная на рис.2в.
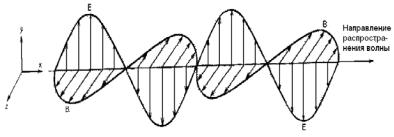
Рис.3 На рис.3 показано изменение напряженности электрического
поля и индукции магнитного поля в пространстве в фиксирован-
ный момент времени; видно, что векторы E и B перпендикулярны друг другу и направлению распространения.
Электромагнитные волны представляют собой поперечные волны и аналогичны другим типам волн. Однако в электромагнитной волне происходят колебания полей, а не веществa, как в случае волн на воде или в натянутом шнуре.
Таким образом, электромагнитные волны генерируются колеблющимися, т. е. движущимися с ускорением, электрическими зарядами. Справедливо и общее утверждение: движущийся с ускорением электрический заряд испускает электромагнитные волны.
4.4.1. Электромагнитные волны и уравнения Максвелла. Скорость распространения электромагнитных волн
Покажем теперь, каким образом существование электромагнитных волн следует из уравнений Максвелла. В этом выводе поражает предсказание не только существования электромагнитных волн, но и той скорости, с которой они должны распространяться.
Рассмотрим область пустого пространства, свободную от элек-
56
трических зарядов и токов проводимости, в такой области вдали от источника волновой фронт (силовые линии на рис.2 в) можно считать плоским на достаточно обширной площади. Такие волны называют плоскими: в любой момент времени электрическое и магнитное поля однородны в плоскости, перпендикулярной направлению распространения. Пусть в выбранной системе координат плоская волна распространяется вдоль оси х со скоростью v , вектор
E направлен по оси у, а вектор B - по оси z (рис.3).
Рис. 4
Бегущую синусоидальную волну с длиной λ и частотой f можно представить в виде
E = Eу = E0 sin (kx - ωt), (4.64)
где
B = Bz = B0 sin(kx - ωt),
k = 2π/λ, ω = 2πf, fλ = ω/k = v |
(4.65) |
и v - скорость распространения волны. Хотя волну для наглядности можно представлять синусоидальной, в дальнейшем это предположение нам почти не понадобится.
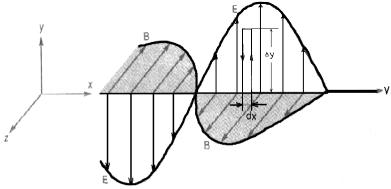
Рассмотрим небольшой прямоугольник в плоскости колебаний
электрического вектора E (рис. 4). Пусть этот прямоугольник имеет конечную высоту y и очень малую ширину dx. Применим к нему закон электромагнитной индукции Фарадея (третье уравнение Максвелла ):
57

|
|
|
|
∫ |
dΦ |
||
Ed = − |
B |
. |
|
dt |
|||
Посмотрим вначале, что представляет собой интеграл по замк-
нутому контуру. Вдоль коротких сторон прямоугольника (длиной dx) вектор E перпендикулярен к d , поэтому E ∙d =0.
Далее, если E - напряженность электрического поля вдоль левой стороны прямоугольника, то вдоль правой стороны напряженность будет несколько больше: E + dE. Итак, если обойти контур против часовой стрелки, то
∫E d = (E + dE)∆y − E∆y = dE∆y .
Скорость изменения магнитного потока через прямоугольник равна
ddtΦB = dBdt dx∆y ,
поскольку площадь контура (dx)(Δy) не изменяется. Возвращаясь к закону Фарадея, получаем
dE∆y = − dBdt dx∆y или dEdx = − dBdt .
Заметим, что E и B являются функциями координаты x и времени t, поэтому следует использовать частные производные:
∂E |
= − |
∂B |
, |
(4.66) |
∂x |
|
∂t |
|
|
где ∂E/∂x обозначает производную E по x при фиксированном t, а ∂B/∂t - производную B по t при фиксированном x.
Подставим в (4.66) уравнения (4.64): kE0∙cos(kx - ωt) = ωB0∙cos(kx - ωt).
Отсюда следует, что E0 = ω = v . А так как E и B изменяются в
B0 k
фазе друг с другом, то и в любой момент времени
E |
= v . |
(4.67) |
|
B |
|||
|
|
58
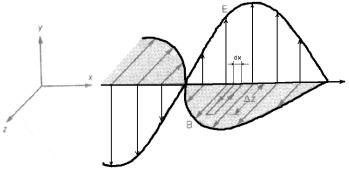
Рис.5 В дополнение к (4.67) можно получить и другое важное соот-
ношение между E и B. Для этого рассмотрим малый прямоугольник в плоскости колебаний вектора индукции магнитного поля В длиной Δz и шириной dx (рис. 5) и применим к нему четвертое уравнение Максвелла (обобщенный закон Ампера):
|
|
|
dΦE |
|
∫ B d =µ0 ε0 |
|
|
||
dt |
||||
(где мы положили I = 0, поскольку токи проводимости отсутству- |
||||
ют). Вдоль коротких сторон |
|
|
|
|
Bd |
= 0, так как вектор B перпенди- |
|||
|
|
|
|
|
кулярен d . Пусть B - индукция магнитного поля вдоль левой |
||||
стороны прямоугольника длиной |
z; тогда вдоль правой стороны |
|||
индукция магнитного поля равна B + dB. Вновь проинтегрируем против часовой стрелки и получим
∫ B d = B∆z −(B + dB)∆z = −dB∆z .
Обратимся теперь к правой части четвертого уравнения Максвелла:
µ0 ε0 ddtΦE =µ0 ε0 dEdt dx∆x .
Приравнивая полученные выражения, имеем
−dB∆z =µ0 ε0 dEdt dx∆z ,
59

или |
∂B |
= −µ |
ε |
dE |
, |
(4.68) |
|
∂x |
0 |
|
0 dt |
|
|
где мы сразу воспользовались записью в частных производных. Возьмем производную по t от (4.68):
|
∂2 B |
= −µ |
ε |
|
∂2 E |
, |
|
|||
|
∂t∂x |
|
|
∂t2 |
|
|||||
|
|
0 |
|
0 |
|
|
|
|
||
и производную по x от (4.66): |
∂2 E |
= − |
|
∂2 B |
. |
|||||
∂x2 |
|
|
∂t∂x |
|||||||
|
|
|
|
|
|
|
||||
В оба полученные соотношения входит ∂2B/∂t∂x, поэтому можно написать
∂2 E |
= |
1 |
∂2 E |
. |
(4.69а) |
|
∂t2 |
µ0 ε0 |
∂x2 |
||||
|
|
|
Взяв другие производные от (4.66) и (4.68), получим аналогичное соотношение для В:
∂2 B |
= |
1 |
∂2 B |
. |
(4.69б) |
|
∂t2 |
µ0 ε0 |
∂x2 |
||||
|
|
|
Уравнения (4.69a) и (4.69б) совпадают по виду с волновым уравнением для плоской волны, распространяющейся в направлении x:
∂22ξ = v2 ∂2 ξ2 . ∂t ∂x
Скорость электромагнитной волны дается соотношением
v2 = |
1 |
. |
|
||
|
µ0 ε0 |
|
Мы видим, что из уравнений Максвелла естественным образом следует тот факт, что E и B подчиняются уравнению для волны,
распространяющейся со скоростью v =1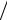

 µ0 ε0 . Именно на этом
µ0 ε0 . Именно на этом
основании Максвелл предсказал существование электромагнитных волн.
Оценим из (33.11) скорость электромагнитной волны
60
