Глава 7. ЭЛЕМЕНТЫ АТОМНОЙ ФИЗИКИ
ИКВАНТОВОЙ МЕХАНИКИ
7.1.Строение атома
В1897 г. Дж. Дж. Томсоном был открыт электрон; им же в 1903 г. предложена затем физическая модель атома, известная под названием «пудинг с изюмом». Согласно модели Томсона атом представлял собой положительно заряженную сферу — пудинг, в котором роль изюминок играли отрицательно заряженные электроны, распределенные так, что вся система в целом была нейтральной.
В 1911 г. бывший ассистент Томсона профессор Эрнест Резерфорд с двумя своими студентами Гансом Гейгером и Эрнестом Марсденом провели рад опытов по рассеянию α-частиц очень тонкой золотой фольгой. Эти знаменитые эксперименты показали несостоятельность модели «пудинга с изюмом» и дали основание Резерфорду высказать предположение, что атом состоит из очень ма-
157
ленького ядра (диаметром около 10-14 м), в котором сосредоточен весь положительный заряд атома, а также большая часть его массы; это ядро окружено облаком из отрицательно заряженных электронов. Поскольку размеры атома порядка 10-10 м, то большая часть пространства в атоме является «пустой»; нейтральность атомов обеспечивается равенством отрицательного заряда электронов и положительного заряда ядра.
Чтобы детальнее изучить строение атома, рассмотрим опыт Резерфорда более подробно. Резерфорд предложил бомбардировать тонкую золотую фольгу (Z = 79) быстрыми α-частицами, источником которых служил Ро-214. Исследовав углы рассеяния (отклонения) α-частиц, проходящих через фольгу, можно было определить структуру атомов-мишеней, вызвавших это рассеяние. Сама α- частица представляет собой ядро гелия и состоит из двух протонов и двух нейтронов. В то время не было еще известно о существовании нейтронов, однако Резерфорд и Томас Ройдс уже в 1909 г. определили, что заряд α-частицы равен 2e.
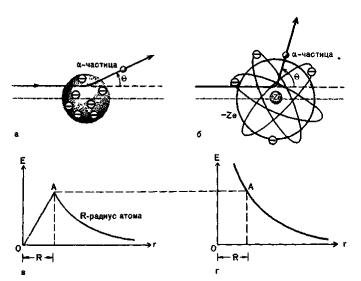
Резерфорд провел теоретические расчеты углов рассеяния Θ в рамках собственной модели и модели Томсона и сравнил полученные результаты с экспериментом. На рисунке схематически изображены модели Резерфорда и Томсона и показано распределение электрического поля для каждого случая. При проникновении в атом, построенный по Томсону (рис. а, в), α-частица будет лишь незначительно отклоняться от первоначального направления, так как электрическое поле внутри такого атома относительно слабое, в особенности если сравнить его с полем в атоме Резерфорда. На одном и том же расстоянии от ядра электрическое поле в атоме Резерфорда значительно сильнее, поскольку весь положительный заряд атома + Ze сосредоточен в малом объеме ядра и, следовательно, угол рассеяния Θ в данном случае будет больше (рис. б, г).
7.1.1 Планетарная модель
Согласно модели Резерфорда атом имеет очень маленькое, но массивное ядро (размером 10-14 м), несущее заряд + Ze. Вокруг этой центральной области расположены Z электронов нейтрального атома. Диаметр атома имеет порядок 10-10 м, что в 10 000 раз
158
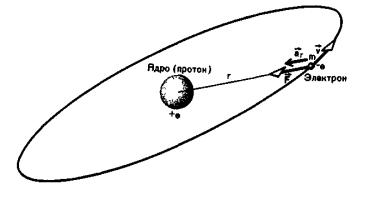
превышает размер ядра. Будем считать эту модель динамической. Если бы модель была статической, то под действием кулоновских сил притяжения все электроны, окружающие ядро, были бы притянуты им. В динамической планетарной модели массивное ядро по существу неподвижно, в то время как электроны движутся вокруг ядра по круговым и эллиптическим орбитам.
Рассмотрим, например, ядерную модель простейшего атома — атома водорода. Для простоты предположим, что электрон (массой m и зарядом —e) движется равномерно по круговой орбите вокруг
протона (с зарядом + e), занимающего центральное положение. В первом приближении движением протона, масса которого почти в 1836 раз больше массы электрона, можно пренебречь.
Сила, удерживающая электрон на орбите, есть сила кулоновского притяжения между протоном и электроном. Эта центральная сила равна:
F = |
1 |
e2 |
, |
(7.1) |
|
4πε0 |
r2 |
||||
|
|
|
где r — радиус круговой орбиты электрона. Из второго закона Ньютона следует, что
1 e2 |
= m |
v2 |
, |
(7.2) |
||
|
|
|
||||
4πε0 r2 |
r |
|||||
|
|
|
||||
159
где ar = v2/r — центростремительное ускорение.
На основании уравнения (7.2) кинетическая энергия электрона в классическом приближении может быть записана как
K = |
1 |
mv |
2 |
= |
1 |
e2 |
. |
(7.3) |
2 |
|
8πε0 |
r |
|||||
|
|
|
|
|
|
Потенциальная энергия системы
U = −eϕ = − |
1 |
e2 |
. |
(7.4) |
|
4πε0 |
r |
||||
|
|
|
Знак «минус» означает, что в данной системе действуют силы притяжения, а не отталкивания, поскольку электрон притягивается к положительно заряженному ядру. Полная энергия системы равна сумме кинетической и потенциальной энергии:
E = K +U = − |
1 |
e2 |
. |
(7.5) |
|
4πε0 |
r |
||||
|
|
|
Знак «минус» показывает, что рассматриваемая система является связанной.
Энергия связи электрона определяется как минимальная энергия, которая требуется для полного удаления электрона из атома, или, другими словами, для ионизации атома. Экспериментальным путем было найдено, что для атома водорода энергия связи равна 13,53 эВ. Подставляя это значение в уравнение (7.5) для E, можно найти радиус r: r = 0,53∙10-10 м = 0,53 А.
Эта величина называется боровским, радиусом (обозначается rb). Ее значение хорошо совпадает со значениями, полученными другими экспериментальными методами.
Линейная скорость v связана с частотой f обращения электрона по орбите соотношением
v =ωr = 2π fr . |
(7.6) |
Подставляя это выражение в уравнение (7.2), получаем:
m(2π fr)2 = 1 e2 ,
4πε0 r
откуда находим частоту обращения электрона вокруг ядра:
160