Формула (4.73) дает мгновенное значение плотности потока энергии электромагнитной волны. Часто бывает необходимо знать среднее значение за длительный промежуток времени. Если E и B изменяются по синусоидальному закону, то среднеквадратичное значение, как и для синусоидальных токов и напряжений, равно

E2 = E02 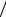2 , где E0 - амплитудное (максимальное) значение напряженности E. Поэтому среднее значение вектора Пойнтинга равно

где B0 - амплитудное значение индукции магнитного поля. Пример 33.3. Плотность потока солнечного излучения, падающего на границу земной атмосферы, равна 1350 Вт/м2. Определите амплитудные значения E и B, считая, что весь поток создается единственной электромагнитной волной.

Решение. Из формулы S =1350 Дж/(с м2 ) =12 ε0cE02 следует, что

=1,01∙103 В/м. B0 = E0/c = 3,4∙10-6 Тл.

Как видно из этого примера, численное значение B очень мало по сравнению с значением E; это различие обусловлено лишь выбором соответствующих единиц и способом их определения. Как мы уже видели, энергия электромагнитной волны поровну распределена между электрическим и магнитным полями.

4.4.4. Импульс электромагнитного поля

Поглощаясь в каком-либо теле, электромагнитная волна сообщает этому телу некоторый импульс, т. е. оказывает на него давление. Это можно показать на следующем примере. Пусть плоская

66

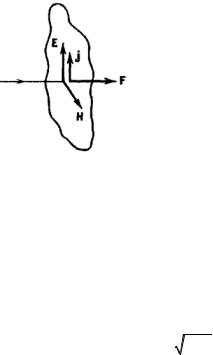
волна падает по нормали на плоскую поверхность слабо проводящего тела ε и μ, равными единице (рис. 9).

Электрическое поле волны возбудит в теле ток плотности

j = σE. Магнитное поле волны будет действовать на ток с силой, величину которой в расчете на единицу объема тела можно найти по формуле (закон Ампера):

F1ob = dVdF = j × B

Направление этой силы, как видно из рис. 9, совпадает с направлением распространения волны.

Поверхностному слою с площадью, равной единице, и толщиной d сообщается в единицу времени импульс

dP = F1ob d = jB d

(векторы j и B взаимно перпендикулярны). В этом же слое в

единицу времени поглощается энергия dW=jEdl, выделяющаяся в виде тепла.

Импульс и энергия сообщаются слою волной. Возьмем их отношение, опустив за ненадобностью символ d:

Отсюда вытекает, что электромагнитная волна, несущая энер-

Из (4.78) следует, что плотность импульса dP/dV = p(т. е. импульс единицы объема) элекгромагнитного поля равна

Плотность энергии связана с модулем вектора Пойнтинга соотношением S = wc. Заменив в (4.76) w через S/c и учтя, что направления векторов P и S совпадают, можно написать

67

4.4.5. Уравнения Максвелла и электромагнитные волны

вматериальной среде

Вприсутствии диэлектриков и (или) магнетиков уравнения Максвелла должны быть несколько видоизменены. Примем для простоты, что среда однородна и изотропна (т. е. обладает одинаковыми свойствами по всем направлениям), а относительная ди-

электрическая проницаемость ε и относительная магнитная проницаемость μ представляют собой константы. Тогда в уравнениях

Максвелла ε0 следует заменить на εε0, а μ0 – на μμ0; заряд Q в первом уравнении Максвелла должен обозначать только свободные заряды.

Скорость распространения электромагнитной волны в этом случае равна

где c - скорость света в пустом пространстве. Поскольку для большинства диэлектриков μ ~ 1, а ε всегда больше единицы, скорость света в среде всегда меньше, чем в вакууме.

В идеальном проводнике (ρ = 0) электрическое поле не может существовать (наличие электрического поля привело бы к возникновению бесконечно большого тока). Поэтому электромагнитная волна не может проникнуть в идеальный проводник и испытывает полное отражение. Действительно, отполированные металлические поверхности хорошо отражают электромагнитные волны и не прозрачны для электромагнитного излучения. В реальный проводник электромагнитные волны проникают на небольшую глубину

(ρ ≠ 0), и возникающие при этом электрические токи приводят к поглощению части энергии волны.

4.4.6. Заключение

Джеймс Клерк Максвелл создал изящную теорию, в которой все явления электричества и магнетизма описываются четырьмя уравнениями -уравнениями Максвелла.

Он основывался на уже известных фактах, дополнив их гипоте-

68

зой о том, что изменяющееся электрическое поле приводит к возникновению магнитного поля. Уравнения Максвелла имеют вид

Первые два уравнения представляют собой закон Гаусса для электрического и магнитного полей; третье-закон электромагнитной индукции Фарадея, четвертое-дополненный Максвеллом закон Ампера.

Теория Максвелла предсказала испускание поперечных электромагнитных волн при ускоренном движении электрических зарядов; электромагнитные волны распространяются в пространстве со скоростью света c. Направления колебаний электрического и магнитного полей в электромагнитной волне перпендикулярны друг другу и направлению распространения волны.

После экспериментального обнаружения электромагнитных волн в конце XIX в. представление о том, что свет является электромагнитной волной (хотя и с гораздо более высокой частотой, чем волны, с которыми проводились опыты в лаборатории), получило всеобщее признание. Спектр (шкала) электромагнитного излучения охватывает очень широкий диапазон длин волн - радиоволны, микроволны, видимый свет, рентгеновское и гамма - излу-

чение; все они распространяются в пространстве со скоростью c = 3,00∙108 м/с.

Энергия, переносимая электромагнитной волной, характеризуется вектором Пойнтинга ,

S= 1 (E × B)

µ0

который определяет плотность потока энергии электромагнитной волны (энергию, переносимую через единицу площади за единицу времени), где E и B -мгновенные значения напряженности электрического поля и индукции магнитного поля в пустом пространстве.

69