22
1 ωmax
2π −ω∫max S(ω) 2 dω = (1−ξ)E1 ,
где ξ – величина, определяющая долю потери энергии вне пределов полосы практической ширины спектра.
2.5.1. Фурье-анализ неинтегрируемых сигналов
Спектральная плотность δ - функции
S(ω) = ∞∫δ(t)e− jωt dt =1
−∞
или δ(t) = |
1 |
∞∫ e jωt dω. |
|
||
|
2π −∞ |
|
Потенциальный сигнал (константа)
S(ω) = ∞∫ Ae− jωt dt = 2π Aδ(ω).
−∞
Спектральная плотность единичного скачка (формула Хэвисайда)
|
|
|
|
|
|
|
|
|
S(ω) = ∞∫σ(t)e− jωt dt =πδ(ω) |
|
− |
1 |
. |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
jω |
|
|
|
||
|
Спектральная плотность гармонического сигнала |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
S(t) = Acos(ω0t +ϕ0 ) . |
|
|
|
|
|
|
|
|
||||||||
|
Воспользуемся формулой (2.16) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
S(ω) = ∞∫ Acos(ω0t +ϕ0 )e− jωt |
= ∞∫ A |
e jω0t+ jϕ0 |
+ e− jω0t− jϕ0 |
|
e− jωt dt = |
|
|
|
||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
−∞ |
|
|
|
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
∞ |
A |
jϕ |
|
− j(ω−ω |
)t |
|
∞ A |
− jϕ |
|
− j(ω+ω |
)t |
|
|
jϕ |
|
|
|
|
|
|
− jϕ |
|
|
|||||
= |
|
|
e |
|
0 e |
0 |
|
dt + |
|
|
e |
|
0 e |
0 |
|
dt = Aπe |
|
0 |
δ(ω −ω0 ) + Aπe |
|
0 |
δ(ω +ω0 ) |
||||||
2 |
|
|
|
−∞∫ 2 |
|
|
|
|
||||||||||||||||||||
−∞∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Спектральная плотность комплексной экспоненты: S(t) = Aexp( jω0t) – сигнал комплексный
S(ω) = 2π Aδ(ω −ω0 ) – спектральная плотность не симметрична!
2.6. Интегральное преобразование Хартли
Для одномерного случая прямое преобразование Хартли может быть определено как [3]
H |
ξ |
) |
= |
∞∫ f (x) |
cos2πξx + sin2πξx dx |
|
( |
|
|
[ |
] |
(2.18) |
|
|
|
|
|
−∞ |
|
и, соответственно, обратное преобра-зование Хартли
f (x) = |
∞∫ H |
ξ |
)[ |
cos2πξx + sin2πξx dξ |
|
|
( |
|
] |
(2.19) |
|
|
−∞ |
|
|
|
23
Сравним эти выражения с (2.6.) и (2.9), разложив ядро по формуле Эйлера на действительную и мнимую части (т.е. sin и cos компоненты):
∞ |
f (x)[cos2πξx − j sin2πξx]dx |
F(ξ) = ∫ |
|
−∞ |
(2.20) |
|
∞
f (x) = ∫ F(ξ)[cos2πξx + j sin 2πξx]dξ
−∞
Из анализа (2.18) - (2.20), можно сделать следующие выводы:
1) Преобразование Хартли является преобразованием с действительным
ядром;
2) Прямое и обратное преобразование Хартли вычисляются идентично; 3) Квадрат модуля преобразования Фурье | F(ν) |2 равен:
F (ν) |
|
2 = H2 (ν) + H2 (−ν) |
(2.9) |
|
|||
|
|
2 |
|
|
|
|
4) Действительная и мнимая компоненты преобразования Фурье могут быть вычислены на основе преобразования Хартли весьма простым образом:
|
|
Re{F(ξ)}= |
|
|
H (ξ)+ H (−ξ) |
|
(2.22) |
||
|
|
|
|
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
Im{F(ξ)}= |
H (ξ)− H (−ξ) |
(2.23) |
|||||
|
|
2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
5) |
Если f(x) - четная (т.е. f(-x)=f(x)), то: |
|
|
||||||
|
|
H (ξ)≡ Re{F(ξ)}, Im{F(ξ)}≡ 0 . |
|
||||||
Основные |
свойства |
преобразования |
Хартли |
соответствуют |
|||||
преобразованию Фурье: |
|
|
|
|
|
|
|
||
1) |
Инвариантность к сдвигу (модуль H2(ξ) + H2(ξ) - неизменен). |
||||||||
2) |
Так же, как и для преобразования Фурье, для преобразования Хартли |
||||||||
справедливы следующие соотношения согласно теореме масштабов: |
|||||||||
|
|
|
f |
( |
) |
|
|
|
|
|
|
|
|
|
x → H(ξ) |
|
|
||
f (mx x)→ H1(ξ) = H(ξ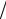
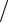mx )
mx
3) Так же, как и для преобразования Фурье, для преобразования Хартли справедлива Теорема Парсеваля.
Отличие от Фурье - преобразования заключается в иной трактовке теоремы о свертке:
Если заданы функции f(x) и g(x), причем H(ξ) и G(ξ) - соответственно их
cпектры Хартли:
f (x) → H(ξ), g(x) → G(ξ),
то их свертка вычисляется следующим образом [3]:
1)вычисляются функции H(− ξ) и G(−ξ);
2)формируется функция: