сферической аберрации положение изображения. В частности, для сферической аберрации 3 порядка при помощи выражений (8.2.9), (8.2.10) можно вычислить положение изображения, в котором кружок рассеяния минимален. При этом продольное смещение изображения составляет 3/4 от продольной аберрации апертурного луча.
8.2.3. Кома
От греческого: κωµα – хвост, пучок волос.
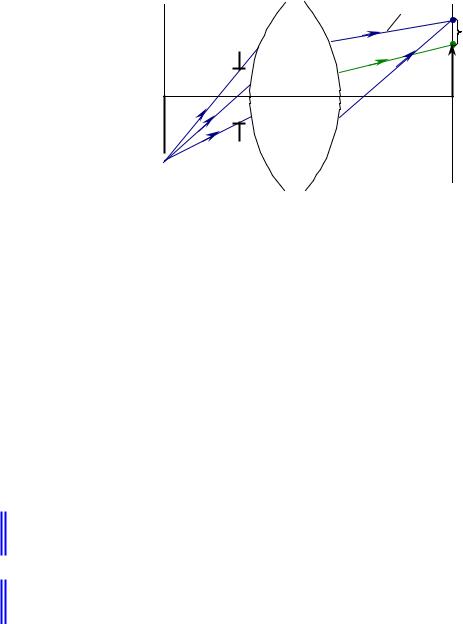
Кома появляется при смещениях точки предмета с оси. Кома добавляется к другим аберрациям (например, к сферической), но мы будем рассматривать ее отдельно от других аберраций (рис.8.2.7).
верхний луч |
A' |
∆y'k |
|
главный луч |
|
|
|
A0 |
' |
|
|
|
y' |
||
|
|
|
|
−y
A 
Рис.8.2.7. Структура пучка лучей при наличии комы.
Впервом приближении кома прямо пропорциональна смещению предмета
соси. Если смещение равно нулю, то и кома равна нулю. Таким образом, поперечная аберрация при наличии комы прямо пропорциональна величине предмета:
∆y'k ~ δ y |
(8.2.12) |
где δ – коэффициент пропорциональности, определяющий качество аберрационной коррекции оптической системы (чем меньше δ , тем лучше оптическая система).
Разложение в ряд волновой аберрации (параграф 8.2.1) при наличии комы 3 и 5 порядков:
W (ρ,ϕ)=W ρ3 cosϕ +W ρ5 cosϕ |
(8.2.13) |
|
31 |
51 |
|
или
W (ρx , ρy )=W31(ρx2 + ρy2 )ρy =W31(ρx2 ρy + ρ3y )
122
Выражение для поперечных аберраций (после выражения (8.2.13)) будет выглядеть следующим образом:
∆x′= λ ∂W A′ ∂ρx
∆y′= λ ∂W A′ ∂ρy
=λ′ W31 (2ρx ρy )
A
=Aλ′ W31 (ρx2 +3ρy2 )
дифференцирования
(8.2.14)
Описание поперечных аберраций комы различно для меридионального и сагиттального сечений. В меридиональном сечении ρx = 0, следовательно:
∆x′ = |
0 |
|
|
|
|
|
|
|
λ |
|
(8.2.15) |
||
|
|
W31 3ρy2 |
||||
∆y′ = |
|
|
|
|
|
|
|
′ |
|
||||
|
|
A |
|
|
||
В сагиттальном сечении ρy = 0 , следовательно: |
|
|||||
∆x′= |
0 |
|
|
|
|
|
|
|
λ |
|
(8.2.16) |
||
|
|
W31 ρx2 |
||||
∆y′ = |
|
|
|
|
||
|
′ |
|
||||
|
|
A |
|
|
||
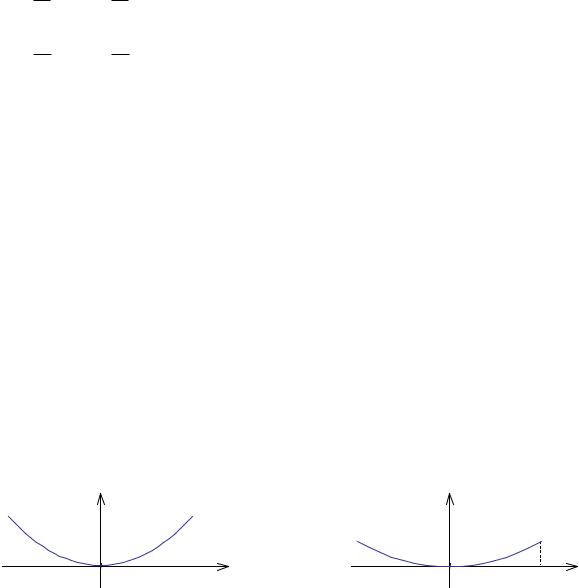
На рис.8.2.8 показаны графики поперечных аберраций для комы 3 порядка в меридиональном и сагиттальном сечениях. Кривые на графиках имеют одинаковую форму, но в меридиональном сечении значение ∆y′ в 3 раза больше, чем в сагиттальном.
|
∆y' |
|
|
∆y′ |
|
|
|
ρy |
|
|
ρx |
-1 |
0 |
1 |
-1 |
0 |
1 |
|
a) меридиональное сечение |
|
б) сагиттальное сечение. |
||
|
Рис.8.2.9. Поперечные аберрации при коме 3 порядка. |
|
|||
Для того чтобы лучше понять структуру поперечных аберраций при коме, рассмотрим точечную диаграмму лучей. Разобьем зрачок на множество равновеликих площадок и рассмотрим лучи, проходящие через центры этих площадок (рис.8.2.10.а). Получим картину лучей, равномерно распределенных по зрачку. Точки пересечения этих лучей с плоскостью изображения образуют точечную диаграмму (рис.8.2.10.б).
123
1 |
ρy |
|
ρx |
|
1 |
а) плоскость зрачка |
|
60o |
y' |
∆y'k |
x' |
б) плоскость изображения |
Рис.8.2.10. Точечная диаграмма.
Кома и неизопланатизм
В названии “неизопланатизм” присутствуют корни греческих слов: изос – одинаковый, равный, планета – блуждающее тело.
Изопланатизм (одинаково заблуждающийся) – в окрестности оси оптической системы нет комы, но есть сферическая аберрация (изображение разных точек предмета будет одинаково плохое). Апланатизм – нет ни комы, ни сферической аберрации (изображение разных точек предмета идеальное). Апланатизм может выполняться только для какой-то части предмета, например
вокрестности оси.
Овозможной величине комы можно судить, не смещая точку с оси, если количественно оценить неизопланатизм. Такая оценка возможна, если использовать условия апланатизма и изопланатизма.
Закон синусов Аббе (условие апланатизма):
sinσ |
= const =V |
(8.2.17) |
|
sinσ′ |
|||
|
|
Если это условие выполняется для всех лучей, то нет ни комы, ни сферической аберрации. Если присутствует сферическая аберрация, то вместо условия апланатизма используется похожее условие – условие изопланатизма:
|
|
|
|
sinσ |
= const =V |
(8.2.18) |
|
|
|
|
|
||
|
|
|
|
sinσ0′ |
|
|
|
|
|
Рис.8.2.11 показывает разницу в определении двух условий – условия |
|||
|
|
|||||
синусов Аббе и условия изопланатизма. |
|
|||||
124