
- •И.Б. Шмигирилова
- •Раздел1. Общая методика
- •Структура теории и методики обучения математике
- •Цели, задачи и функции обучения
- •Общие цели обучения математике
- •Функции обучения математике
- •Задачи обучения математике
- •Составные части содержания обучения и их характеристики Составные части процесса обучения
- •Классификация методов обучения
- •Формы обучения
- •Средства обучения
- •Подготовка урока с использованием средств обучения
- •К контроль и оценка знаний
- •Урок - основная форма обучения
- •Конечный результат урока (кру)
- •Состав комбинированного урока и содержание его этапов
- •Типология уроков
- •Требования к современному уроку
- •Психологические требования
- •Виды анализа урока
- •Самоанализ урока
- •Программа оценки эффективности урока
- •Планирование урока. Пример конспекта урока 1.
- •Пример конспекта урока 2.
- •Математические понятия. Методика работы над определением.
- •Пример правильной классификации
- •Виды определений
- •Методика работы над определением.
- •Технологическая цепочка формирования математических понятий
- •Составление родословной понятия
- •Теорема. Виды теорем. Методика работы над теоремой
- •Классификация методов доказательства по пути обоснования тезиса
- •Классификация методов доказательства по математическому аппарату, используемому при доказательстве
- •Организация работы над теоремой
- •Технологическая цепочка изучения теоремы
- •Задачи в обучении математике Различные определения понятий «задача» и «проблема»
- •Учебная и познавательная задачи
- •Процесс решения задачи
- •Решение задач с позиции деятельностного подхода
- •Процесс решения задачи
- •Как решать задачу
- •Сравнение задач на нахождение и задач на доказательство
- •Различные классификации задач
- •Функции задач в обучении математике
- •Раздел 2. Частная методика
- •Технологическая цепочка изучения числовых множеств.
- •Специальные приемы решения задач по теме
- •Методические особенности изучения линии тождественных преобразований выражений
- •Технологическая цепочка формирования обобщенных приемов тождественных преобразований выражений
- •Учебные цели изучения линии тождественных преобразований
- •Специальные приемы решения задач по теме
- •Методические особенности изучения линии уравнений и неравенств
- •Распределение линии уравнений и неравенств по классам
- •Учебные цели изучения линии уравнений и неравенств
- •Технологическая цепочка обучения решению уравнений
- •Вопрос о равносильности уравнений
- •Специальные приемы решения задач по теме
- •Методические особенности изучения функциональной линии
- •Распределение функциональной линии по классам
- •Учебные цели изучения функциональной линии
- •Технологическая цепочка изучения свойств функций
- •Методические особенности вероятностно-статистической линии в средней щколе
- •Распределение вероятностно-статистической линии классам
- •Учебные цели изучения вероятностно-статистической линии
- •Геометрическая линия школьного курса математики Цели и задачи изучения геометрической линии школьного курса математики
- •Функции школьного курса геометрии Требования к геометрической подготовке учащихся средней школы
- •Литература
- •Оглавление
- •Раздел1. Общая методика……………………………..4
- •Раздел 2. Частная методика………………………….91
Технологическая цепочка обучения решению уравнений

Замечание: аналогическая цепочка строится для обучения решению неравенств с дополнительным использованием при этом сравнения с уравнениями.
Вопрос о равносильности уравнений
|
Равносильность сохраняется
f(x) = g(x) (f(x))2b-1 = =(g(x))2b-1
(a > 0, a1) Появляется теоретически в 10-11 классах после изучения показательной функции, перед решением показательных уравнений. |
Равносильность может быть нарушена 1. Если обе части уравнения умножить на h(x), то f(x) = g(x) ? h(x)f(x) = h(x)g(x)
2. Если обе части уравнения возвести в четную степень. f(x) = g(x) ? (f(x))2b = (g(x))2b
|
Специальные приемы решения задач по теме
-
Тип задачи
Алгоритм выполнения приема
1
2
Поиск решения уравнения (неравенства, системы, совокупности)
Определить по виду уравнения (неравенства, системы, совокупности) и прикидкой, каким методом можно воспользоваться.
Вспомнить известный (специальный или общий) прием использования этого метода и соотнести его с данным уравнением (неравенством, системой, совокупностью).
Определить возможные затруднения при использовании одного метода решения.
определить возможность и необходимость комбинации различных методов решения.
Разделить предполагаемый ход решения на части, соответствующие применению каждого метода, составить план решения каждой из них.
Составить общий план решения в целом.
Решение уравнения (неравенства, системы, совокупности) алгебраическим методом
Определить, является ли данное уравнение (неравенство, система, совокупность) простейшими какого-либо вида (если «да», то выполнить п. 5, если «нет» - п. 2).
Определить, если необходимо, ОДЗ уравнения (неравенства, системы, совокупности).
Установить, какие и в каком порядке необходимо выполнить тождественные и равносильные (общие или специальные для данного вида уравнений или неравенства) преобразований, чтобы привести данное уравнение (неравенство, систему, совокупность) к простейшим данного вида.
Выполнить выбранные преобразования, используя соответствующие приемы.
Решить известным способом (по формулу, алгоритму), полученные уравнение (неравенство, систему, совокупность).
Если необходимо сделать проверку и исследование.
Записать ответ, используя принятые приемы записи (в виде равенств, промежутков, их объединений или пересечений).
1
2
Специализация общего приема на основе конкретизации третьего этапа решения уравнений и неравенств алгебраическим методом
На примере показательных уравнений и неравенств.
Определите, является ли это уравнение (неравенство) простейшим вида
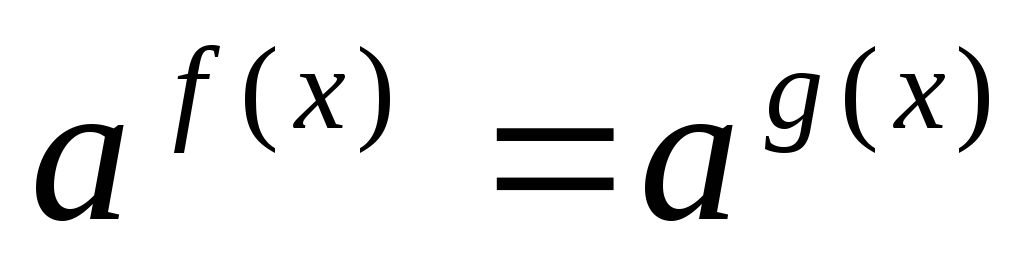 (
(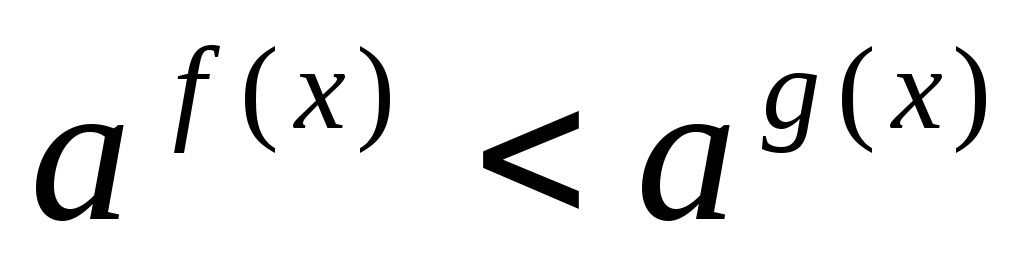 или
или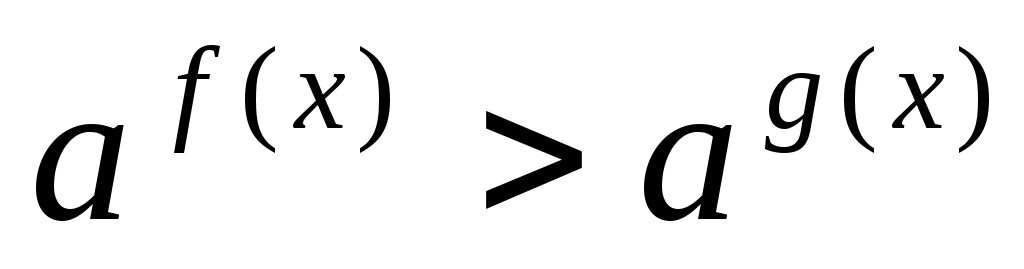 ):
если «да», то п. 4, если «нет», - п. 2.
):
если «да», то п. 4, если «нет», - п. 2.Установить, какие и в каком порядке нужно выполнить тождественные и равносильные преобразования (общие для всех уравнений или неравенств или специальные, основанные на свойствах степени или показательной функции), чтобы привести уравнение (неравенство) к простейшему.
С помощью выбранного преобразования привести уравнение (неравенство) к простейшему виду.
Заменить уравнение (неравенство) равносильным алгебраическим уравнением
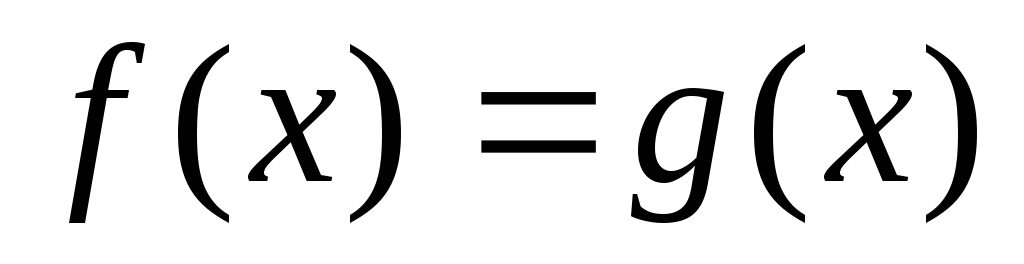 (неравенством:
при
(неравенством:
при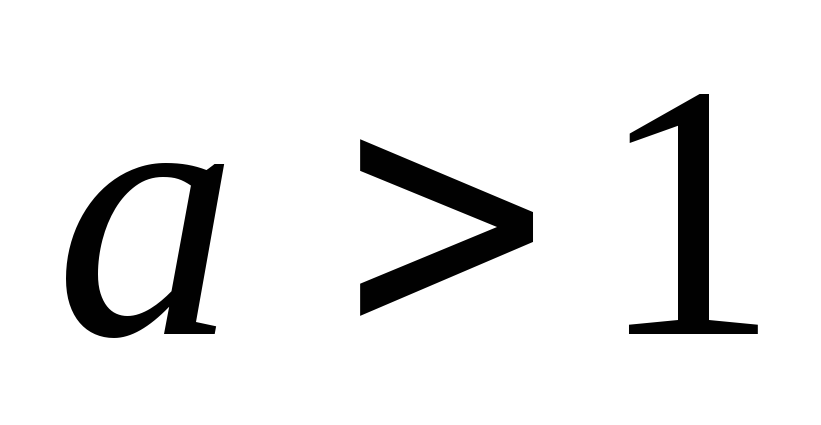 -
-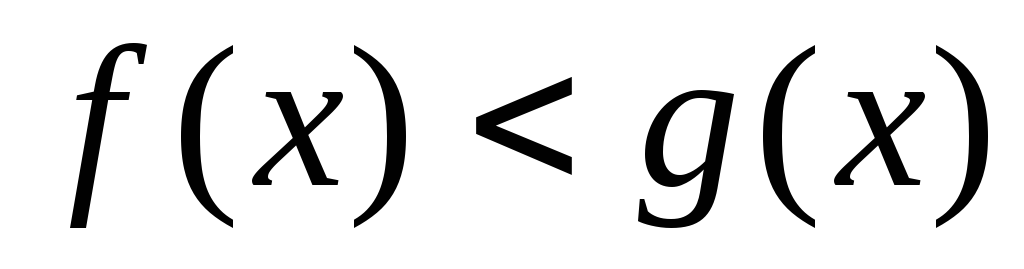 или
или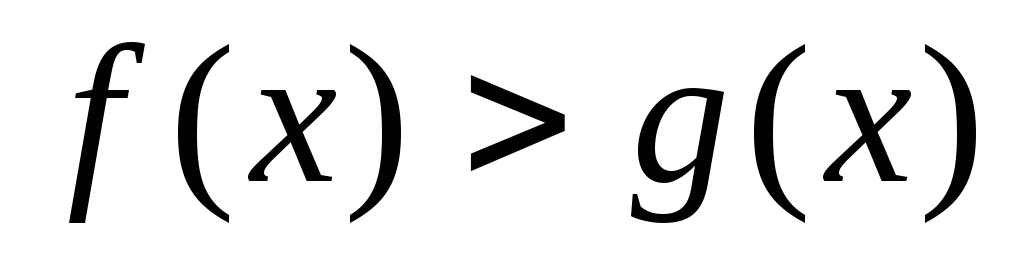 ;
при
;
при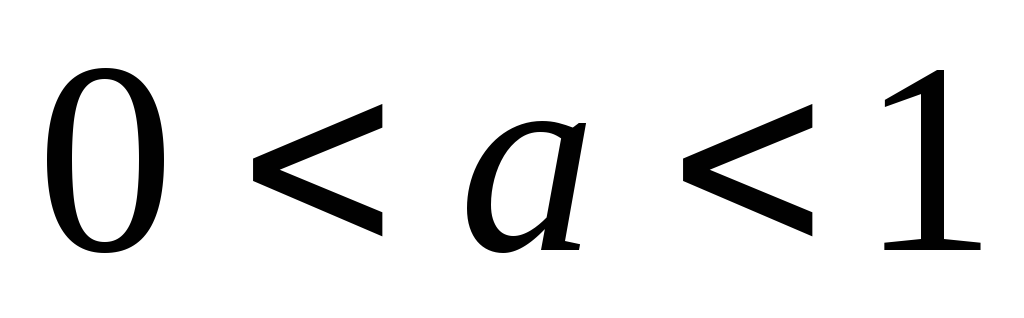 -
-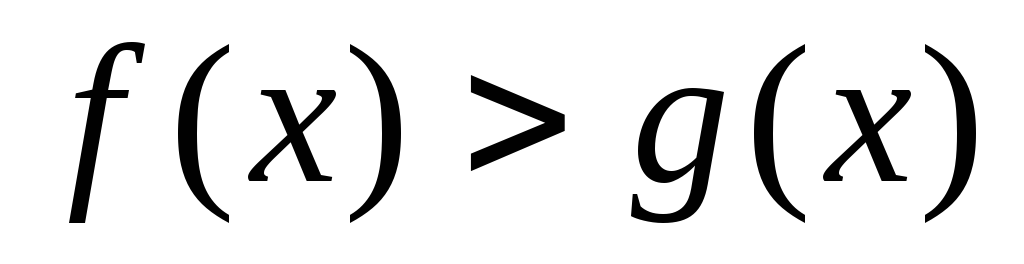 или
или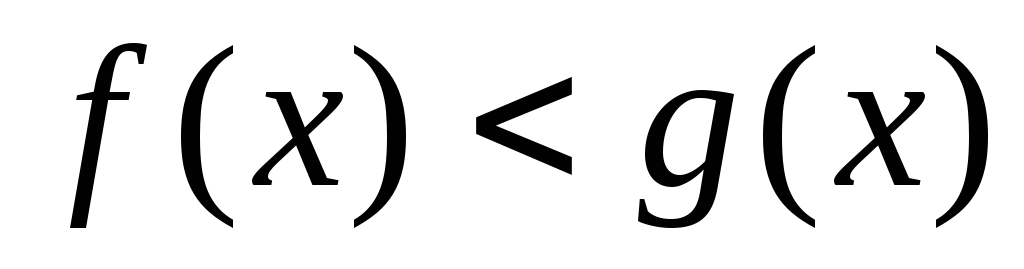 ).
).Решить полученное уравнение (неравенство), используя соответствующий прием.
Если нужно, сделать проверку и исследование.
Записать ответ.
Замечание: Аналогичны приемы решения целых, дробно-рациональных, иррациональных, логарифмических и тригонометрических уравнений и неравенств.
1
2
Решение уравнения (неравенства) графическим методом
Определить, можно ли преобразовать каким-либо способом уравнение (неравенства) к виду
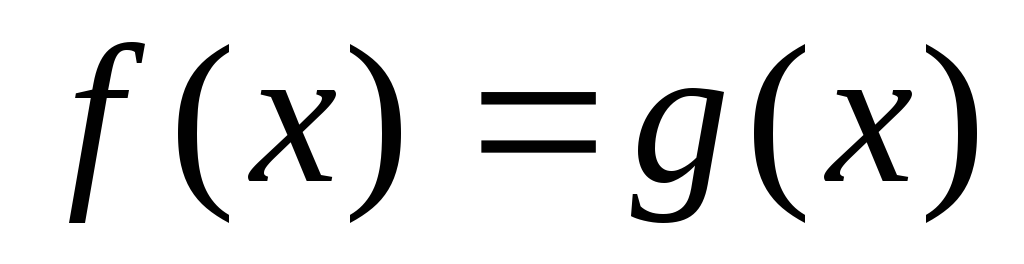 (
(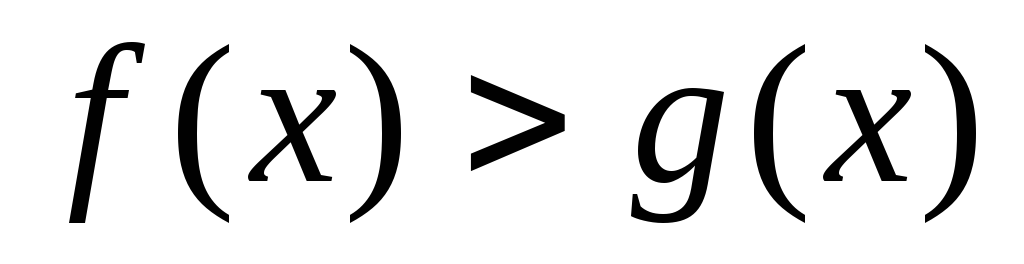 ).
).Если п. 1 имеет место выполнить преобразования, выбрав
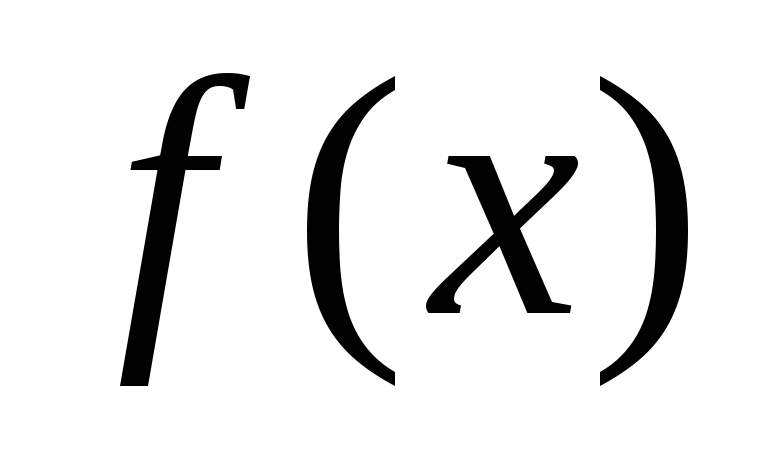 и
и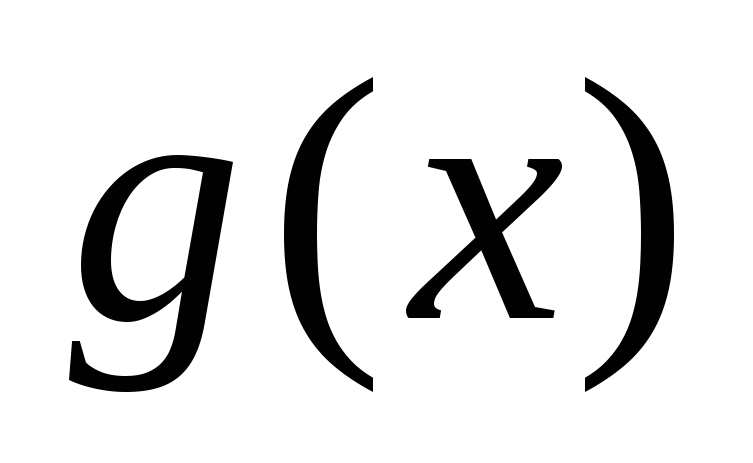 наиболее
простого вида.
наиболее
простого вида.Построить графики функций
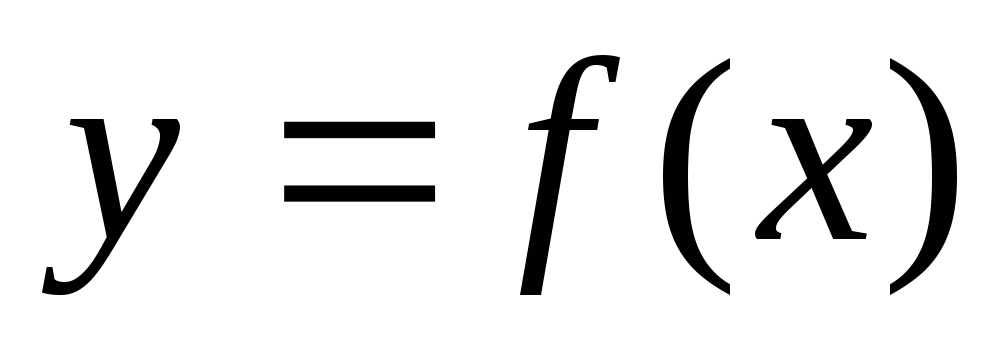 и
и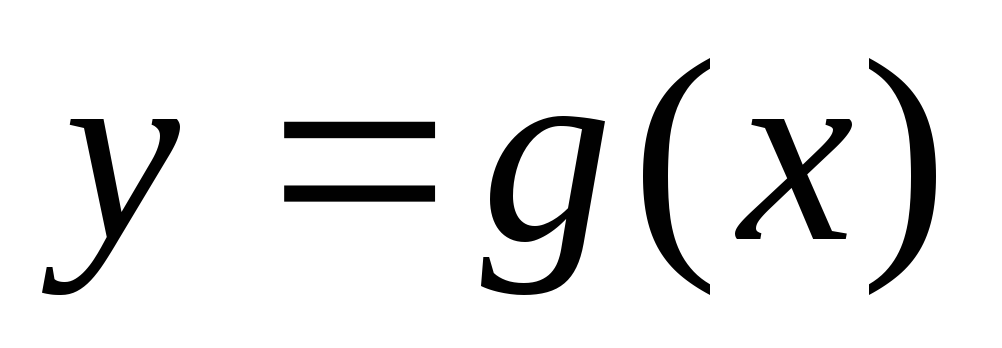 в
одной системе координат.
в
одной системе координат.Найти абсциссы точек пересечения графиков, каждая из них – корень данного уравнения.
Найти промежутки на оси абсцисс, для которых график функции
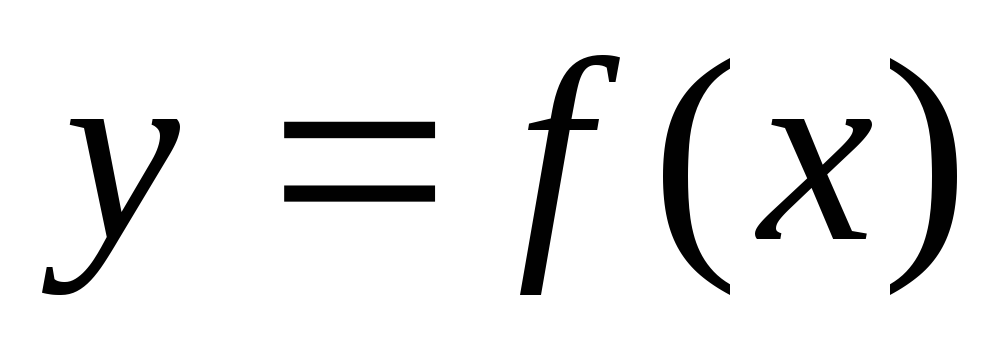 расположен выше графика функции
расположен выше графика функции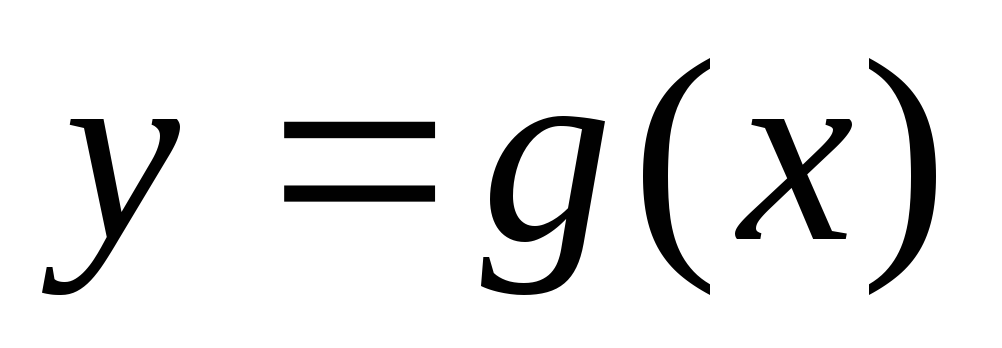 ,
каждый из них есть решение данного
неравенства.
,
каждый из них есть решение данного
неравенства.Записать ответ.
Определить, можно ли каким-либо способом преобразовать неравенство к виду
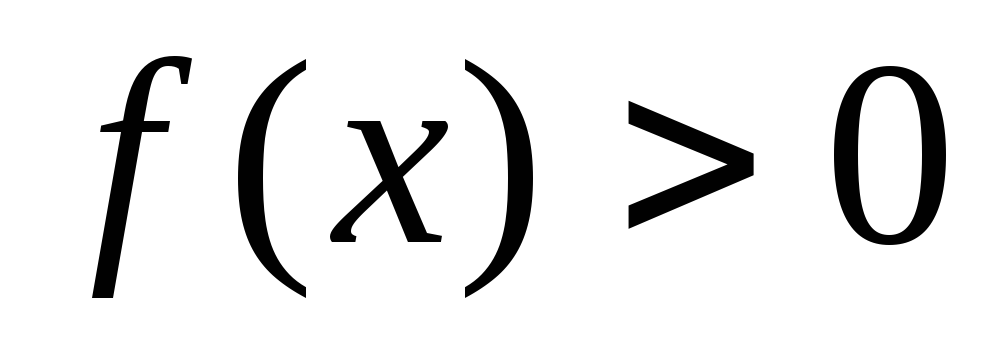 или
или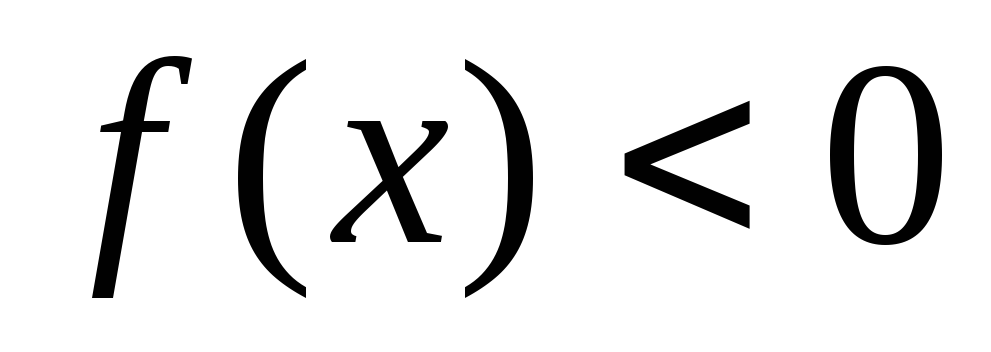 .
.Если п. 1 имеет место, выполнить преобразование, выбрав
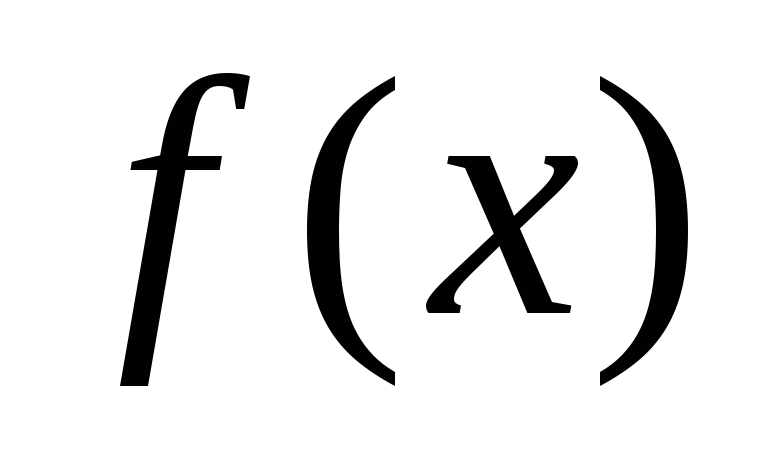 наиболее простого вида.
наиболее простого вида.Найдите корни функции
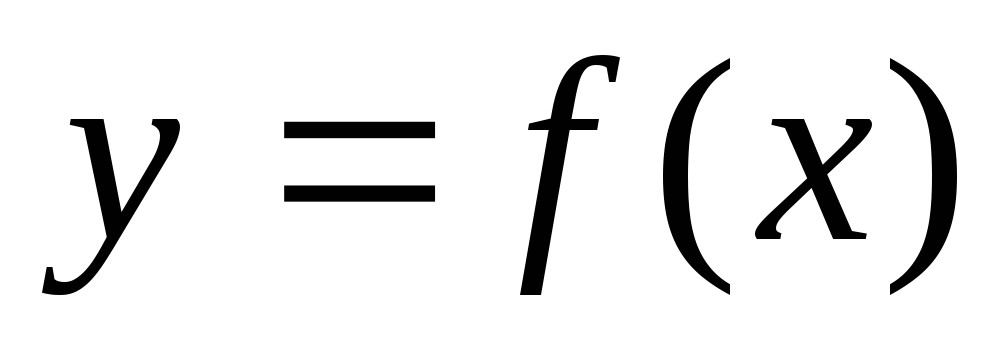 в области ее непрерывности и точки
разрыва, если они существуют.
в области ее непрерывности и точки
разрыва, если они существуют.Отметить полученные значения на числовой оси.
Определить знак функции
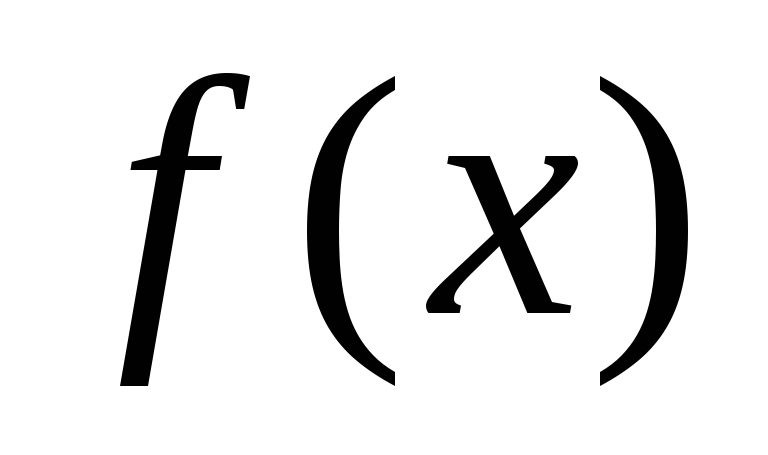 на
каждом из полученных интервалов
числовой оси (вычислением значения
функции в удобной точке интервала
или на основании теоремы о свойстве
непрерывной функции).
на
каждом из полученных интервалов
числовой оси (вычислением значения
функции в удобной точке интервала
или на основании теоремы о свойстве
непрерывной функции).Выбрать интервалы, на которых функция принимает нужное по знаку значение и записать ответ.
