
Turanov_Bondarenko_Vlasova_Kreplenie_gruzov_v_vagonakh
.pdfof fastening cargo has been realized on the basis of considering the mechanical system «cargo-fastening-wagon» as problems indeterminations static.
Such approach permitted us to find not only exertions in flexible elements of fastening, but also the displace of cargo long wide and transverse concerning to the axis of symmetry of a wagon. This permitted use to determinate places of fixing persistent bars, as the extra elements of cargo fastenings. In this connection there have been distinguished (in this manual) theory, method, program and results of calculation exertions in flexible elements of fastenings of cargoes with flat base, taking into consideration climatic conditions of transportation and simultaneous acting of longitudinal, transverse and vertical forces, and using abilities of MathCAD.
In the manual it is taken into consideration, that the consigner is only a user of the program of calculating exertions in not interested in the theoretical provision. So this program has been developed program the consigner has only to insert such data as mass, geometrical parameters of concrete cargo and also projections of flexible elements of fastening on the long wide, transverse and vertical axis. Then pushing the button «Control” + End» on a keyboard of a computer he can get the most value of exertions in the flexible elements of fastenings axes and its possible rotation around the vertical axis.
So, the calculation of exertions in the flexible elements fastenings of cargoes is full automatic and a consigner becomes free from difficult calculations. It proves the incontestable profit of this method.
In the ninth chapter «Calculation of strength of supports» there is given the consequence of the testing calculation of strength of the supports and given the concrete example.
In the tenth chapter «Permissible loads on the elements of wagons construction» on can find requirements to the ways of fastening, characteristics of elements of fastening and cargo regulating values on permissible loads on elements of wagon construction (by Specs.) and results of calculation of weld in devices, used for fastening cargoes. There are also distinguished requirements to the ways of fastening and of cargo using Specs. for allocation and fastenings cargoes in wagons and containers.
In the eleventh chapter «Fastening cargoes of cylindrical form and cargoes on wheels» there are formulae to calculate the fastening of cargoes of cylindrical form and cargoes on wheels with their next derivations. There are also given some remarks about derivation of final analytical formulae in Specs.
In the twelfth chapter «Overall and oversize cargoes in a wagon» there are general points, conditions and procedures of oversize cargos transportations, degree and area determination of oversize cargoes. There are also given determination analysis of oversize cargoes.
Thus, in the manual there are distinguished specific properties of cargoes and wagons for transportation and modern theory solving a wide range of tasks of rational allocation and the consequence of calculating flexible elements of cargoes fastening.
20
I. ОСНОВНЫЕ ФОРМУЛЫ МАТЕМАТИКИ И ПРИКЛАДНОЙ МЕХАНИКИ
BASIC FORMULAE OF MATHEMATICS AND APPLIED
MECHANICS
В данном разделе приведены основные формулы и понятия из элементар- ной математики, физики и прикладной механики (теоретическая механика и со- противление материалов), которые широко применяются при решении при- кладных задач дисциплины «Крепление грузов в вагонах» и необходимые для дальнейшего изучения этой дисциплины.
Ознакомление с основными понятиями данного подраздела в дальнейшем позволит легко освоить раздел дисциплины «Крепление грузов в вагоне», ка- сающиеся анализа равновесия и взаимодействия грузов и расчета гибких (упру- гих) элементов креплений груза в вагоне.
1.1. Основные формулы элементарной математики
Basic formulaу of elementary mathematics
1.1.1. Основные формулы тригонометрии
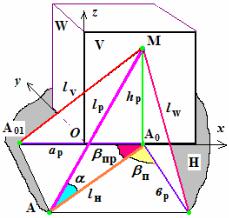
Для примера рассмотрим пространственно расположенный AMA0, ребро (катет) MA0 которого опирается на тело (например, груз) прямоугольной формы
(рис.1.1).
Причем вершина М этого треугольника (или монтажная петля груза) расположена на любой высоте hр боковой грани (вертикальной плоско- сти) рассматриваемого тела (груза). Пусть ребро (катет) AA0 этого треугольника расположен на
горизонтальной плоскости H и его вершина А (например, увязочное устройство или стоечная скоба вагона) лежит на некотором расстоянии от вертикальной плоскости V (например, от боковой грани груза).
Рис.1.1. К определению угла наклона и проекции
пространственно расположенной линии АМ
На рис. 1.1 обозначены: α – угол наклона нити АМ к горизонтальной плос- кости H (например, к полу вагона); βпр и βп – углы между проекцией AA0 линии АМ (например, длины растяжки - lр) на горизонтальную плоскость H и соответ- ственно вертикальной (продольной) V и фронтальной (поперечной) W плоско- стей; aр, вр, hр – проекции нити АМ (растяжки) на продольную - х, поперечную - у и вертикальную - z оси, которые подлежат определению расчетом (или же непосредственным замером из схемы размещения груза в вагоне). Иначе hр –
21

высота точки закрепления растяжки на грузе относительно уровня пола вагона (подкладок). Пусть lH, lV, lW – проекции нити АМ (т. е. длины растяжки − lр) на горизонтальную − H, фронтальную – W и вертикальную – V плоскости.
Если известны проекции нити АМ на продольную, горизонтальную и вер- тикальную оси в виде aр, вр, hр (см. рис.1.1), то можно отыскать значения функ-
ции одного угла8:
sinα = |
hр |
|
cosα = |
|
l |
H |
cos βпр |
= |
aр |
|
sin |
βпр = |
вр |
|
; |
||||||
lр |
|
|
|
lн |
|
lH |
|
||||||||||||||
|
|
lр |
|
||||||||||||||||||
|
; |
|
|
|
|
; |
|
|
|
; |
|
|
|
|
|
|
|||||
cos βп = |
вр |
, |
tgα = |
hр |
|
ctgα = |
l |
H |
|
|
|
|
|||||||||
|
lH ; |
|
|
|
(1.1) |
||||||||||||||||
lH |
hр |
; |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
где lH - проекция нити АМ на горизонтальную плоскость - H (т. е. длины рас- тяжки к полу вагона), м:
|
|
|
|
lH = a2р + в2р ; |
(1.2) |
||
lр – длина нити АМ (т.е. растяжки), м:
|
|
|
|
lр = a2р + в2р + hр2 . |
(1.3) |
||
Учитывая формулу (1.1), можно получить произведение функции двух уг-
лов:
cosα cosβпр = |
l |
H |
|
aр |
= |
aр |
, |
(1.4) |
lр |
|
lH |
lр |
|||||
|
|
|
||||||
cosα sin βпр = |
|
l |
H |
|
|
вр |
= |
|
вр |
|
. |
||||
|
lр |
|
|
lH |
|
lр |
|
||||||||
|
|
|
|
|
|
|
|
||||||||
cosα cos βп = |
l |
H |
|
|
вр |
|
= |
вр |
|
. |
|||||
|
lр |
|
lH |
lр |
|||||||||||
|
|
|
|
|
|
||||||||||
►Основные формулы приведения тригонометрических функций: sin(-α) = - sin(α); cos(-α) = cos(α);
tg(-α) = - tg(α); ctg(-α) = - ctg(α).
(1.5)
(1.5,а)
(1.6)
8 Бронштейн И.Н., Семендяев К.А. Справочник по математике. − М.: Наука, 1964. – 608 с.
22
Функции |
β = 900 ±α |
β =1800 ±α |
β = 2700 ±α |
β = 3600 ±α |
sinβ |
cosα |
m sinα |
- cosα |
- sinα |
cosβ |
m sinα |
- cosα |
± sinα |
cosα |
tgβ |
m ctgα |
± tgα |
m ctgα |
- tgα |
ctgβ |
m tgα |
± ctgα |
m tgα |
- ctgα |
►Основные формулы тригонометрии |
|
|
|
||
● функции одного угла - |
sinα |
|
cosα |
|
|
sin2 α + cos2 α = 1, |
= tgα, |
= ctgα, |
|||
cosα |
sinα |
||||
tgα × ctgα = 1; |
|
|
|||
|
|
|
(1.7) |
||
● выражение функции одного угла через другую функцию (того же угла)
|
|
|
|
tgα |
|
|
|
1 |
|
|
|
sinα = 1− cos2 α , sin α = |
|
, |
sinα = |
|
, |
||||||
|
|
|
|
|
|
||||||
1+ tg 2α |
|
1+ ctg 2α |
|||||||||
|
|
|
|
|
|
|
|
||||
|
α = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
ctgα |
|
||||||||||
cos |
1 |
− |
sin |
2 |
α |
, |
|
|
|
α = |
|
|
|
|
|
|
cosα = |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
cos |
|
1+ tg 2α , |
|
1+ ctg 2α |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
sinα |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||||
|
|
tgα = |
|
|
|
|
|
, |
|
tgα = |
1− cos |
2 |
α , tgα = |
|
|
|
, |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ctgα |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
1− sin 2 α |
|
|
|
|
|
|
|
|
|
cosα |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
cosα |
|
|
1 |
. |
|
|
|
|
||||||||||||||||||||||
α = |
|
1− sin |
2 α |
|
|
|
|
|
α = |
|
|
|
|
ctgα = |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
ctg |
|
|
sinα |
|
|
|
, |
ctg |
|
|
|
|
1− cos2 α , |
|
|
|
|
|
|
|
tgα |
|
|
|
|
|||||||||||||||||
1.1.2. Основные формулы геометрии:
Теорема косинусов (рис.1.2,а):
,
(1.8)
a2 |
= b2 |
+ c2 − 2bccos β ; |
|
b2 |
= a2 |
+ c2 − 2accosγ ; |
|
c2 |
= a2 + a2 − 2abcosα . |
(1.9) |
|
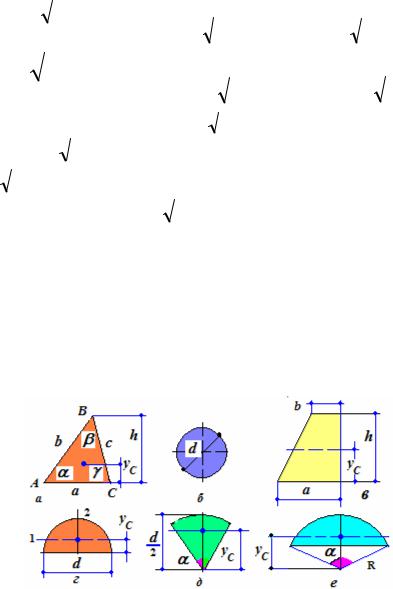
Рис.1.2. К определению координат центров тяжести различных фигур
Приводим формулы определения площади для простейших форм плоских сечений (см. рис. 1.2):
23

-треугольника (рис.1.2,а) – S = ah/2;
-круга (рис.1.2,в) - S = πd2/4;
-трапеции (рис.1.2,в) - S = [(a+b) /2] h;
-кругового сектора (рис.1.2,д) -
S = |
πd 2 |
α |
|
|
|
, |
|
4 |
3600 |
||
где d – диаметр и α – половина центрального угла (в град.) кругового сектора; - кругового сегмента (рис.1.2,е) –
S = |
d 2 |
( |
πα |
− sinα ) , |
|
8 |
1800 |
||||
|
|
|
где d – диаметр и α − центральный угол дуги (в град.) кругового сегмента.
1.2. Основные понятия и формулы физики и теоретической механики9
Basic notions and formulaу of Physics and Theoretical Mechanics
1.2.1. Центр тяжести Сenter of gravity
►Точка приложения силы тяжести тела называется центром тяжести тела. На рисунках центры тяжести обозначаются через С (англ. − Centre, амер.
− Center).
►При перемещениях и поворотах центр тяжести тело не изменится.
Знание положения центра тяжести груза позволяет найти оптимальную схему крепления груза при транспортировке. При определении положения цен- тра тяжести объемных грузов, имеющих постоянное поперечное сечение по длине, используются формулы координат центров тяжести соответствующей плоской фигуры. При определении величины внутренних усилий в связях и де-
формируемых элементах креплений используются различные геометрические характеристики, вычисляемые относительно центральных осей, проходящих через центр тяжести рассматриваемого плоского поперечного сечения.
Приводим формулы определения координат центров тяжести для простейших форм плоских сечений
(рис. 1.2):
для треугольника (см. рис.1.2,а) –
yC = h3
или
xC |
= |
xA + xB + xC |
; |
|
|||
1 |
3 |
|
|
|
|
|
|
9 Воронков И.М. Курс теоретической механики. − М.: Наука, 1966. − 596 с.
24

yC |
= |
yA + yB + yC |
, |
|
3 |
||||
1 |
|
|
||
|
|
|
где h – высота треугольника;
xA, xB, xC и yA, yB, yC – координаты вершин данного треугольника;
для трапеции (см. рис.1.2,в) –
yC = |
a + 2b |
h, |
|
3(a + b) |
|||
|
|
где h, a и b– соответственно высота, большое и малое основание трапеции;
для полукруга (см. рис.1.2,г) –
yC = 0.2122d,
где d – диаметр полукруга;
для кругового сектора (см. рис.1.2,д) –
yC = 3600 d sin3αα ,
где d – диаметр и α - половина центрального угла (в град.) кругового сектора; для кругового сегмента (см. рис.1.2,е) –
yC = 1.33 |
Rsin3 |
α |
, |
2α |
|
||
|
|
|
3600 - sin 2α
где R и α – радиус и угол (в рад.) кругового сегмента.
В случае более сложных плоских фигур и объемных тел используется метод разбиения: рассматриваемое тело разбивается на совокупность тел, для которых легко определить положение центра тяжести. Координаты
центра тяжести составного тела определяются по однотипным формулам
|
|
|
n |
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
||
|
|
= |
å xi Ai |
|
|
|
|
= |
|
å yi Ai |
|
|
|
|
|
|
|
||
x |
С |
i |
, |
y |
С |
|
i |
|
|
, |
|
|
|
|
|||||
n |
|
n |
|
|
|
|
|
|
|||||||||||
|
|
|
å Ai |
|
|
|
|
|
|
å Ai |
|
|
|
|
|
|
|
||
|
|
|
i |
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
||
|
|
|
n |
|
|
|
|
|
|
n |
|
|
|
|
|
n |
|
||
|
|
= |
å xiVi |
|
|
|
|
= |
å yiVi |
|
|
|
|
= |
å ziVi |
|
|||
x |
С |
i |
|
, |
y |
С |
|
i |
|
, |
z |
С |
i |
, |
|||||
n |
|
n |
n |
||||||||||||||||
|
|
|
åVi |
|
|
|
|
|
|
åVi |
|
|
|
|
|
åVi |
|
||
|
|
|
i |
|
|
|
|
|
|
i |
|
|
|
|
|
i |
|
||
где i – номер тела, n – количество тел разбиения, Ai – площадь плоской i-той фигуры разбиения, Vi – объем i- того тела разбиения, xi, yi, zi – координаты центра тяжести i-того тела разбиения относительно выбранной об- щей системы координат.
При наличии отверстий в сечении или полостей в объемном теле приведенные формулы можно ис- пользовать, полагая соответствующие площади или объемы отрицательными.
1.2.2. Понятие о силе
Notions of a Force
При изучении дисциплины «Крепление грузов в вагонах» и решении при- кладных задач используются следующие понятия о силе.
25
Сила в механике есть мера механического взаимодействия тел, физиче-
ская величина, характеризующая интенсивность взаимодействия тел, в резуль- тате которого изменяется их состояние (движения или равновесия) или их фор- ма.
Сила (англ. – Force) – векторная величина, характеризуемая точкой прило- жения, величиной и направлением действия. Сила обозначается буквой F. Едини-
цей измерения силы является Н (Ньютон), кН (кило Ньютон) в Международной системе единиц измерения (СИ) или тс (тонна сила) в технической системе единиц, которая все еще широко используется на железнодо- рожном транспорте (см., например, гл.1 ТУ).
Силу можно перенести по ее линии действия, не изменяя действия данной силы на тело (в дальнейшем для нашего случая - груз) (следствие аксиомы при- соединения). Это утверждение справедливо только для недеформируемых тел.
Силы, с которыми действуют друг на друга два тела, всегда равны по мо- дулю и направлены по одной прямой в противоположные стороны (аксиома действия и противодействия).
Сила тяжести (вес тела) (англ.– Force of Gravitation), действующая на тело, равна произведению массы тела на ускорение свободного падения G = mg (из- меряется в Н, при m – масса тела в кг, g – ускорение свободного падения в м/с2).
1.2.3. Связи и их реакции
Constraints and reactions constraint
При изучении дисциплины «Крепление грузов в вагонах» любая практиче-
ски важная задача связана с определением неизвестных реакций внешних связей. В частности, усилия в гибких упругих элементах креплений груза механической системы «груз − крепления − вагон» подлежат определению, через неизвестные реакции внешних связей, с использованием основных положений и принципов теоретической механики.
Практически все тела (грузы), равновесие или движение которых рассмат- ривается в технических приложениях, являются несвободными, т. е. они всегда либо опираются на другие тела, либо связаны с другими телами (грузами) и/или опорной плоскостью посредством других тел, например, гибких креплений, различных подкладок, упоров.
Тела, которые ограничивают движение рассматриваемого тела, в механике называют связями (англ. – constraint).
Связи в механике бывают внешние и внутренние.
По отношению к объекту равновесия или движения связи в механике под- разделяются на внешние и внутренние.
Простейшим примером несвободного тела является крупнотоннажный контейнер, рассматриваемый как твердое тело. Нижние отверстия у нижних фитингов контейнера используются для постановки его на упоры специализи- рованной платформы или автомобильного полуприцепа (рис.1.3,а). Здесь для контейнера рама специализированной платформы или пол автомобильного по- луприцепа являются внешними связями.
26
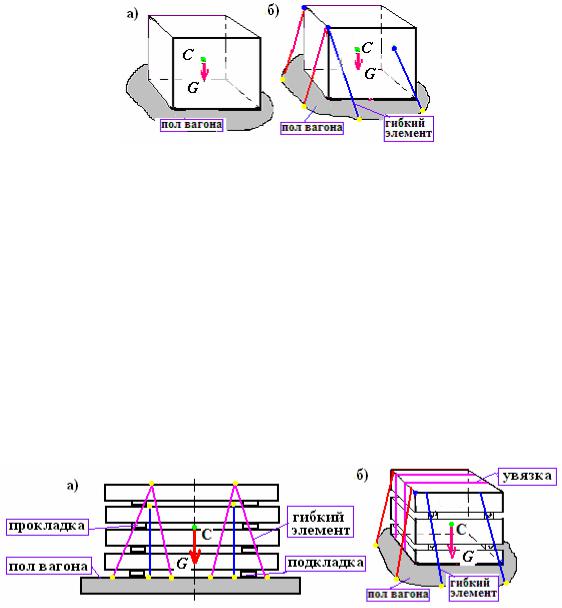
Другим примером является штучный груз (твердое тело) весом G, опи- рающийся на платформу и закрепленный к нему n гибкими элементами крепле- ний (растяжками) (рис.1.3,б).
Рис.1.3. К пояснению связей
Для данного примера внешними связями являются платформа и гибкие элементы креплений (растяжки, обвязки) для штучного груза (см. рис.1.3,б). Здесь пол платформы не дает грузу перемещаться по вертикали вниз, а гибкие
элементы креплений ограничивают перемещения груза по плоскости пола платформы.
Для штабельного груза (рис.1.4,а), расположенного в вагоне несколькими ярусами и закрепленного к нему гибкими элементами креплений, внешними
связями для верхних ярусов являются ниже расположенные единицы грузов (материальные тела) и гибкие элементы креплений. В то же время при рассмот- рении всего штабельного груза в качестве объекта равновесия первые упомяну- тые связи (ниже расположенные единицы грузов, как и выше расположенные) являются внутренними (ограничивают взаимные перемещения).
Рис.1.4. К пояснению связей
Другим примером подобной ситуации является укрупненное грузовое ме- сто, образованное из единиц грузов и рассматриваемое как система твердых тел, объединяемых в одно целое посредством увязок. Такая система опирается на пол платформы и закрепляется гибкими элементами креплений (рис.1.4,б). Здесь увязки и прокладки являются внутренними связями. Гибкие элементы по- прежнему являются внешними связями.
Примером, обладающим внутренней связью, также является конструкция балки, состоящая из системы двух твердых тел АК и КЛ, соединенных шарни- ром в точке К (рис.1.5). Здесь шарнир К является внутренней связью, соеди-
27
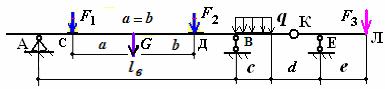
няющей две балки, на которые действуют внешние сосредоточенные силы F1, F2, F3 и распределенная сила q.
Рис.1.5. К пояснению внутренней связи
Таким образом, связи в механике могут быть внешними и внутренними, в виде материальных тел, твердых и гибких.
Тело (груз) под действием приложенных на него внешних сил (продоль- ных, поперечных и вертикальных переносных сил инерции и силы давления ветра) стремиться к перемещению по опорной поверхности (пол вагона). Одна- ко связь (пол вагона) будет препятствовать этому перемещению тела. Поэтому тело будет действовать на связь с некоторой силой, называемой силой давления Q на связь. Одновременно по аксиоме равенства действия и противодействия связь будет действовать на тело с такой же по модулю, но противоположно на- правленной силой N, т. е. N = Q. Это справедливо только для случая, когда груз (контейнер) размещен в вагоне без применения гибких элементов креплений.
Сила, с которой тело (пол платформы), осуществляющее связь, действует на данное рассматриваемое тело (штучный груз), препятствуя его перемеще- нию в том или ином направлении, называется реакцией (противодействием) этой связи. Согласно принципа освобождаемости тела от связей, любое несво- бодное тело можно сделать свободным, если отбросить связи и их действие заменить соответствующими реакциями.
Реакцией (англ. − Reaction) связи для объекта, показанного на рис.1.3,а, представляемой виде гладкой поверхности является N - нормальная состав- ляющая реакции связи (англ. − Normal reaction of constraint). Для реальной сис- темы опирания контейнера с установкой фитингов на упоры, препятствующие горизонтальному смещению, рассматривают две компоненты равнодействую- щей полных реакций от каждого из упоров – N и R, где N – вертикальная (нор- мальная) и R – горизонтальная составляющие.
Примечание: 1. Для свободно лежащего на платформе груза (см. рис.1.3), согласно аксиоме равенства действия и противодействия, сила тяжести груза G и нормальная составляющая реакции связи N имеют равные модули и противо- положные направления, т. е. N = G.
2. Для закрепленного в вагоне гибкими элементами крепления груза (см. рис.1.3,б и 1.4) N > G, поскольку груз от сдвига удерживается еще и предвари- тельно натянутыми гибкими элементами крепления. Точка приложения равно- действующей реакции связи N может быть смещена относительно проекции центра масс груза на пол вагона вследствие несимметричности постановки свя- зей и схемы нагружения. При этом координаты точки приложения равнодейст- вующей xN и уN подлежат определению, так же как величина реакции связи N, из условий равновесия механической сиcтемы «груз – крепления – пол вагона».
28
3. После замены связей реакциями связи на объекте они не показываются
(см. рис.1.4).
2) Для механической системы «груз − крепление − вагон», где груз закреп- лен в вагоне гибкими элементами (см. рис. 1.3,б и 1.4), N > G, а координаты приложения реакции связи xN и уN смещены относительно проекции центра тя- жести груза на плоскость пола вагона. Так происходит потому, что груз от
сдвига удерживается еще и предварительно натянутыми гибкими элементами креплений.
Определение реакции связей является одной из наиболее важных задач статики, широко встречающиеся в теории размещения и крепления грузов в ва- гонах и контейнерах.
Рассмотрим наиболее распространенные виды связей, встречающиеся в за- дачах статики.
1.Связь в виде гладкой (т. е. без трения) плоскости или поверхности
(рис.1.3,а). В этом случае реакция связи N всегда направлена по общей нормали
копорной поверхности.
2.Связь в виде контакта цилиндрической или шаровой поверхности
(рис.1.7).
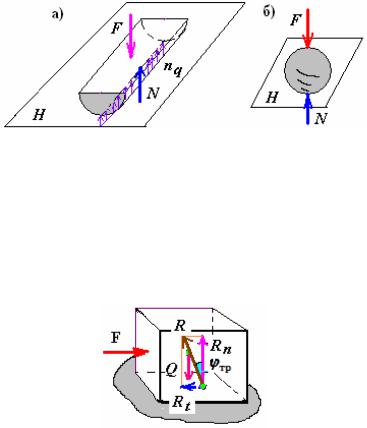
Рис. 1.7. Связь в виде контакта криволинейных поверхностей с плоскостью
В этом случае реакция связи N (для цилиндрической поверхности, как ре-
зультирующая сила равномерно распределенной по длине цилиндра реакции связей nq) также направлена по нормали к опорной поверхности.
3. Связь в виде шероховатой поверхности (рис.1.8).
Рис. 1.8. Связь в виде шероховатой поверхности
Здесь от силы тяжести G груза и от действия на груз внешней силы F воз- никают две составляющие реакции связей: нормальная Rn, перпендикулярной к плоскости, и касательная Rt, лежащая в плоскости. Касательная реакция связи
29
