4. Моменты инерции относительно параллельных осей.

Пусть известны моменты инерции фигуры относительно осей,:

; ;

.

Требуется определить моменты инерции относительно осей , параллельных центральным

; ;.

Координаты любой точки в новой системе :

; .

Подставим эти значения в формулы для моментов инерции и проинтегрируем почленно:

;

;

.

Интегралы икак статические моменты относительно центральных осей и формулы преобразования моментов инерции относительно параллельных осей принимают вид:

; ;.

Момент инерции фигуры относительно любой оси равен моменту инерции относительно центральной оси, параллельной данной, плюс произведение площади фигуры на квадрат расстояния между этими осями.

Центробежный момент инерции относительно любой системы прямоугольных осей равен центробежному моменту относительно системы центральных осей, параллельных данным, плюс произведение площади фигуры на координаты ее центра тяжести в новых осях.

5. Зависимости моментов инерции при повороте

координатных осей.

Пусть известны моменты инерции произвольной фигуры (рис. 17) относительно осей,:

; ;

.

Повернем оси ,на уголпротив часовой стрелки, считая угол поворота осей в этом направлении положительным.

Найдем моменты инерции сечения относительно повернутых осей ,:

; ;.

Координаты произвольной элементарной площадки в новых осях:

;

.

Подставим эти выражения в формулы для моментов инерции и проинтегрируем почленно:

;

;

.

Итак,

; ; .

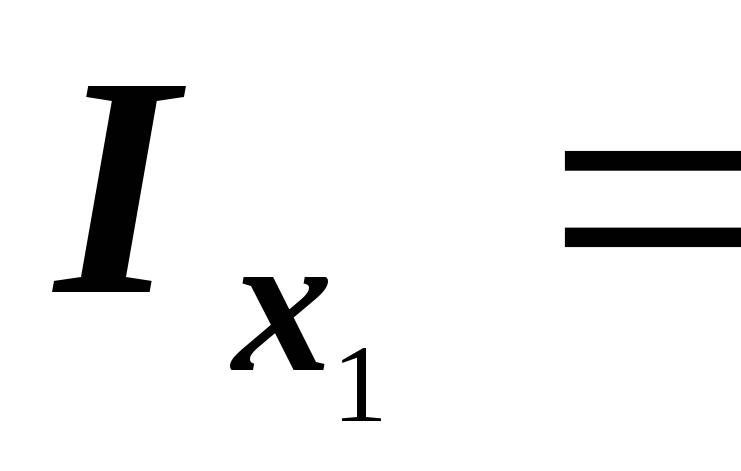
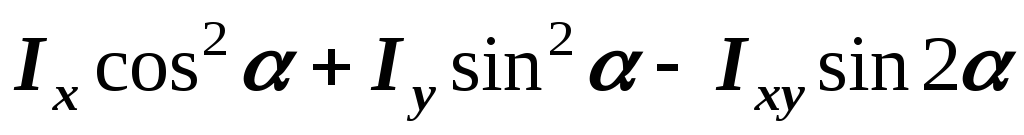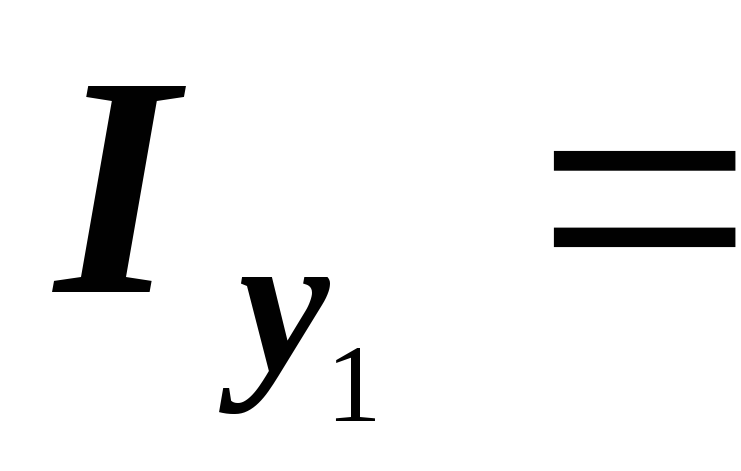
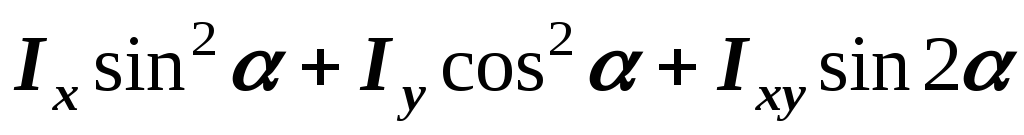Формулы, полученные при повороте любой системы прямоугольных осей, справедливы и для центральных осей.

Складывая почленно, получим:

.

При повороте прямоугольных осей сумма моментов инерции не меняется и равна полярному моменту инерции относительно начала координат.

6. Определение направления главных осей.

Главные моменты инерции.

Наибольшее практическое значение имеют главные центральные оси, центробежный момент инерции относительно которых равен нулю. Обозначим такие оси ,. Следовательно,

.

Если фигура имеет ось симметрии, то эта ось и другая, перпендикулярная к ней, проходящая через центр тяжести фигуры, являются главными центральными осями.

Чтобы определить положение главных центральных осей несимметричной фигуры, повернем произвольную начальную систему центральных осей,(рис. 18) на некоторый угол, при котором центробежный момент инерции становится равным нулю.

.

Используя формулу преобразования центробежного момента инерции при повороте осей, получим:

Рис. 18.

.

Откуда

или .

Если , то поворот осуществляется против часовой стрелки.

Значения главных моментов инерции можно получить из общих формул перехода к повернутым осям, приняв :

;

.