8. Обобщенный закон Гука.

Выделим элементарный параллелепипед главными площадками. Примем, что материал изотропен. Возникающие деформации малы по сравнению с размерами деформируемого параллелепипеда. Деформации упругие. Все это дает возможность применить принцип независимости действия сил к вычислению деформаций.

Положим, что на элементарный параллелепипед действуют только нормальные напряжения . Тогда согласно закону Гука удлинение в направлении оси равно:

Укорочение в направлении осей и :

Полагая, что действуют только нормальные напряжения , найдем

Деформации от действия напряжения

Нормальные напряжения вызывают изменения длин ребер.

Предположим, что на выделенный элемент действуют только касательные напряжения (рис. 92). Их действие сопровождается искажением формы элемента.

Касательные напряжения будут вызывать изменение прямого угла в плоскости на угол сдвига.

Аналогично, от действия касательных напряжений имеем:

от касательных напряжений

При наличии всех компонент напряжений деформации:

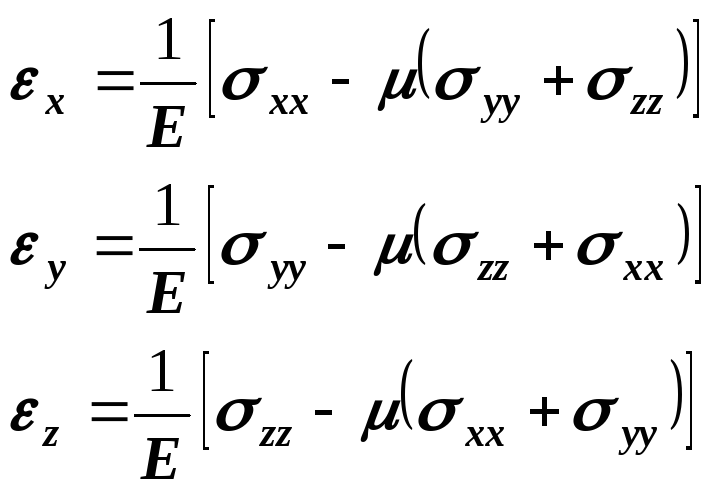
(16)

Полученные уравнения называются обобщенным законом Гука.

9. Потенциальная энергия деформаций.

Главными плоскостями выделим элементарный куб с размерами ребер равными 1. Действие отброшенных частей заменим силовыми факторами.

Т.к. площадки главные, то по граням куба будут действовать только нормальные напряжения (рис. 93).

Так как силовые факторы, действующие по главным площадкам совершают работу только по своему направлению, то к определению величины удельной потенциальной энергии деформации можно применить закон независимости действия сил. Нам известно, что при линейном напряженном состоянии зависимость между напряжениями и деформациями линейна (рис. 94), поэтому удельную потенциальную энергию деформаций можно определить:

При объемном напряженном состоянии удельная потенциальная энергия определится:

об.н.сост.

(17)

В общем случае нагружения удельную потенциальную энергию деформации можно записать:

- удельная потенциальная энергия изменения объема,

- удельная потенциальная энергия изменения формы.

Для определения потенциальной энергии изменения объема, заменим данное напряженное состояние на другое: (рис. 95).

Вэтом случае будет меняться объем без изменения формы элемента. Удельные потенциальные энергии изменения объема будут равны для двух рассматриваемых напряженных состояний, если равны их объемные деформации.

Относительная объемная деформация элементарного куба в первом случае нагружения равна:

Выражая относительные линейные деформации по формулам обобщенного закона Гука, получим:

Удельная потенциальная энергия изменения объема:

или (18)

или

(19)

Потенциальная энергия деформации и общие

МЕТОДЫ ОПРЕДЕЛЕНИЯ ПЕРЕМЕЩЕНИЙ

1. Свойства упругих тел

Упругой называется система, деформирующаяся под действием внешних нагрузок, а после их снятия полностью восстанавливающая первоначальную форму и размеры.

1. При нагружении упругой системы внешними силами точки приложения сил в результате деформации системы перемещаются, и силы совершают работу .

В процессе деформации изменяется взаимное расположение частиц в системе, накапливается потенциальная энергия . За счет этой энергии после снятия нагрузки восстанавливается первоначальная форма и размер системы.

Поскольку в упругой системе восстановление полное, можно считать, что численно работа внешних сил, затраченная на деформацию, равна потенциальной энергии упругой деформации

(1)

Это основное свойство упругой системы, которое используется во всех энергетических методах расчетов.

2. Упругие системы являются линейно деформируемыми, то есть всякое перемещение пропорционально силе, его вызвавшей.

(2)

Например:

Если нагрузкой является момент, то соответствующие перемещения будут пропорциональны моменту; пропорциональность справедлива как для линейных, так и для угловых перемещений.

К упругим системам применим принцип независимости действия сил. Следовательно, всякое перемещение в системе можно вычислять как сумму

перемещений от каждой нагрузки отдельно (рис. 97).

Часто перемещение от произвольной силы приходится выражать через перемещение от единичной силы:

пусть - перемещение от силы,

- перемещение от силы = 1,

тогда .

Принцип независимости действия сил применим при вычислении внутренних силовых факторов и напряжений, но не справедлив при вычислении работы.