2. Моменты инерции плоских фигур.

Осевыми моментами инерции площади фигуры называют выражения

; .

Полярным моментом инерции площади фигуры относительно полюса называют

.

Если через полюс проведена система взаимно перпендикулярных осейи(рис. 10), то(как гипотенуза).

Тогда

,

то есть полярный момент инерции относительно полюса равен сумме осевых моментов инерции относительно осей, проходящих через полюс.

Отметим, что величины осевых и полярных моментов инерции положительны.

Центробежным моментом инерции называют . Единицы измерения осевых, полярных и центробежных моментов инерции -.

Центробежный момент инерции может быть положительным, отрицательным и равным нулю.

Оси, относительно которых центробежный момент инерции равен нулю, называют главными осями. Две взаимно перпендикулярные оси, одна из которых является осью симметрии фигуры, называются главными осями. Главные оси, проходящие через центр тяжести сечения, называются главными центральными осями.

Вычислим моменты инерции прямоугольника относительно центральных осей, параллельных его сторонам (рис. 11).

Выделим элементарную площадку в виде узкого прямоугольника, параллельного оси. Площадь элемента.

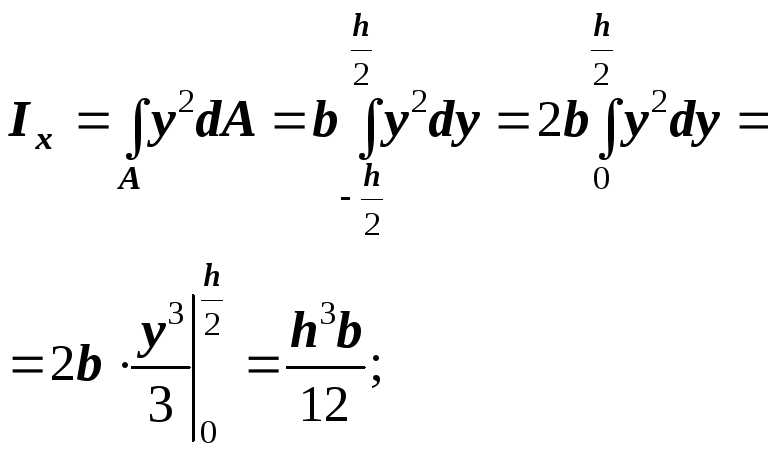
Аналогично, если выделить элементарную вертикальную полоску шириной , получим:и

.

Вычислим полярный момент инерции круга относительно его центра, а также момент инерции относительно центральной оси.

При вычислении полярного момента инерции выделим элементарную полоску в виде тонкого кольца толщиной (рис. 12). Площадь такого элемента равна

Ввиду малости слагаемым пренебрегаем.

Полярный момент инерции

.

В силу симметрии фигуры . Используя свойство осевых и полярных моментов инерции, получим: . Отсюда

.

3. Моменты инерции сложных сечений.

В расчетной практике часто приходится вычислять моменты инерции сложных сечений. Для прокатных профилей (рис. 13) геометрические характеристики сведены в таблицы, которые называются сортаментом прокатной стали.

Рис. 13.

двутавр

швеллер

Равнобокий уголок

неравнобокий уголок

Пусть требуется определить моменты инерции сложной фигуры относительно осей ,(рис. 14). При вычислении моментов инерции сложных сечений их нужно разбить на простые части, моменты инерции которых известны.

Из основного свойства интеграла суммы следует, что момент инерции сложной фигуры равен сумме моментов инерции составных ее частей.

;

.

Если в сечении имеется отверстие (рис. 15), то его удобно считать фигурой с отрицательной площадью.

;

.