2. Изгиб с растяжением (сжатием)

К двутавровой балке приложена сила параллельная оси (рис. 138).

Рассмотрим какие силовые факторы дает силав произвольном сечении:

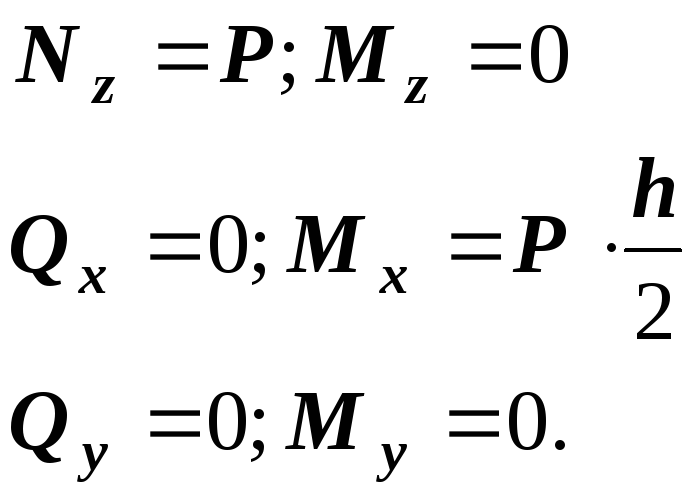
Возникает два силовых фактора: растягивающая сила и момент, изгибающий балку в вертикальной плоскости. Напряжения вычисляются отдельно от каждого силового фактора и складываются. Строим эпюры напряжений.

Максимальные напряжения действуют в верхних точках, это опасные точки. Нейтральная ось смещена от центра тяжести сечения.

Пример: Проверить прочность балки (рис. 139).

Строим эпюрыи, чтобы определить опасное сечение, в которомимаксимальные.– опасное сечение.

В опасном сечении находим опасные точки, в которых иимеют одинаковые знаки и складываются. Опасные точки сверху.

Записываем условие прочности

3. Косой изгиб. Пространственный изгиб.

Косой изгиб. Пространственный изгиб.

Вобоих случаях нагружения в сечениях будет действовать по две пары силовых факторов: изгибающие моменты и поперечные силы в двух главных плоскостях. Силы,учитывать не будем.

Рассматривая косой изгиб для удобства положительным будем считать момент, вызывающий в первом координационном углу растягивающие напряжения.

1. Напряжения в произвольной точке (рис. 142):

, берутся со знаками.

2. Нулевая линя или нейтральная ось – линия в точках которой напряжения равны нулю .

.

Получили уравнение прямой, проходящей через начало координат.

Для частного случая косого изгиба (рис. 143).

Получаем, что , то есть нейтральная ось не перпендикулярна силовой линии при. Только в частном случае(круг и квадрат) ось и сила будут перпендикулярны.

3. Максимальные напряжения возникают в точках, наиболее удаленных от нейтральной оси. Для прямоугольных сечений и сечений, вокруг которых можно описать прямоугольник, это угловые точки. Их координаты являются ,для сечения.

Условие прочности:

.

Для проверки прочности при косом или пространственном изгибе нужно построить эпюры в двух главных плоскостях и по ним определить опасные сечения, в которых иодновременно или в отдельности имеют максимумы.

Величины идля каждого сечения берут по эпюрам.

Нельзя в условия прочности подставлять моменты максимальные из разных сечений, так как это не будет соответствовать условиям нагружения.

4. Прогиб при косом изгибе вычисляется отдельно от изгиба в каждой плоскости, а затем производиться геометрическое сложение (рис. 145).

.

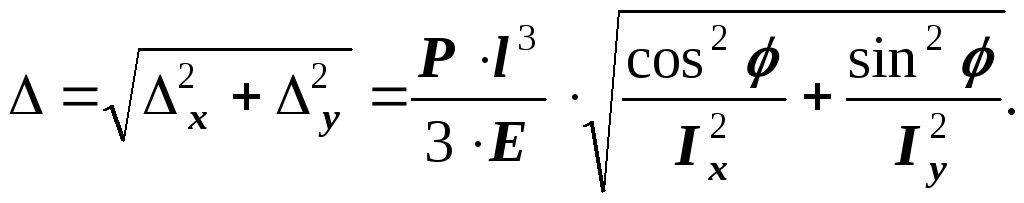
–направление прогиба при косом изгибе не совпадает с направлением силы (рис. 147), отсюда и название “косой” изгиб. Косого изгиба не бывает в круглом и квадратном сечении, так как и.

Прогиб всегда перпендикулярен нейтральной оси, так как п.ч.

Для высоких и узких сечений /двутавр, прямоугольник/ и,(рис. 147). Косой изгиб опасен, так как даже при малом отклонении силы от вертикали может возникнуть большой прогиб в направлении малой жесткости, и произойдет потеря устойчивости изгиба.