4. Условие прочности при растяжении. Типы задач.

Основная задача сопротивления материалов - обеспечить надежные размеры детали при действии на нее различных нагрузок. Такие размеры можно определить из расчета на прочность. Прочность стержня при осевом растяжении обеспечена, если для каждого его поперечного сечения выполняется условие прочности:

- абсолютное значение продольной силы; - площадь поперечного сечения;

- допускаемое напряжение при растяжении или сжатии для материала стержня.

, где - коэффициент запаса. Для пластичных материалов предельным напряжением является предел текучести, а для хрупких материалов - предел прочности.

Условие прочности при растяжении или сжатии заключается в том, что наибольшее расчетное напряжение в элементе конструкции не должно превосходить допускаемого напряжения.

С использованием условия прочности выполняются три вида расчетов:

1. Проверочный расчет (проверка прочности). При заданных нагрузках и площади поперечного сечения определяют расчетное напряжение и сравнивают его с допускаемым . Превышение расчетного напряжения по сравнению с допускаемым не должно превышать 5 %, иначе прочность рассчитываемой детали считается недостаточной.

2. Проектировочный расчет (подбор сечения). По известным нагрузкам и допускаемому напряжению определяют необходимые размеры поперечного сечения

.

3. Определение допускаемой нагрузки. По известным размерам и материалу детали определяют допускаемую нагрузку .

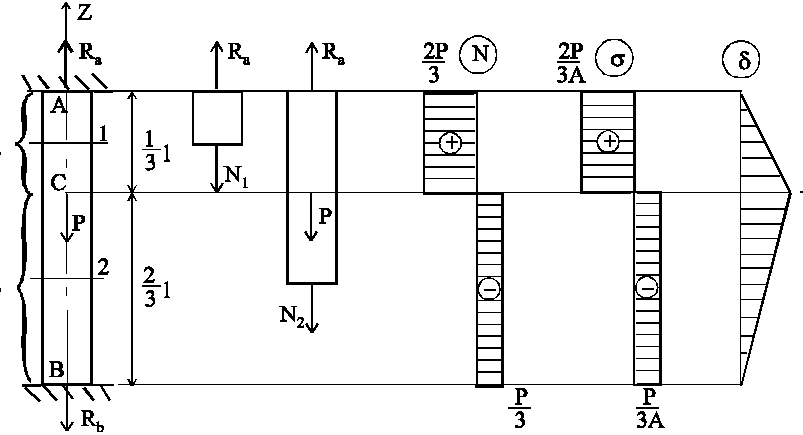
5. Статически неопределимые конструкции.

Статически неопределимыми называются такие конструкции, в элементах которых при помощи только одних уравнений статики определить усилия невозможно. Кроме уравнений статики для расчета таких конструкций необходимо использовать также уравнения, содержащие деформации элементов конструкций. Эти уравнения называются уравнениями совместности деформаций.

В статически неопределимых конструкциях число неизвестных, подлежащих определению, больше, чем число уравнений статики, которые можно составить для данной системы. Разность между числом неизвестных и числом уравнений статики называется степенью статической неопределимости.

Последовательность расчета статически неопределимых систем рассмотрим на примере:

Задание: Прямой однородный стержень, имеющий постоянную площадь поперечного сечения , закреплен по концам и нагружен силой(рис. 36). Построить эпюры продольных сил, нормальных напряженийи продольных перемещений точек - границ участков. Модуль продольной упругости материала.

1

Рис. 36.

. Находим степень статической неопределимости:

(система один раз статически неопределима).

2. Составляем уравнение статики: ..

3. Разбиваем брус на участки. Границами участков являются точки приложения сосредоточенных сил, сечения, в которых изменяется площадь.

4. С использованием метода сечений выражаем продольные силы на участках через одну опорную реакцию.

1 - й участок: ..;

2 - й участок: ...

5. Составляем уравнение совместности деформаций участков бруса. Так как концы бруса жестко защемлены, то его общая длина не изменяется, т.е.

.

6. Записываем выражения закона Гука, выражая абсолютные деформации участков через усилия, возникающие в поперечных сечениях

.

7. Подставляем выражения закона Гука в уравнение совместности деформаций

= 0.

Отсюда ;

; ;.

8. Определяем продольные силы на участках и строим эпюру .

(растяжение); (сжатие).

9. Определяем нормальные напряжения и строим эпюру .

(растяжение); (сжатие).

10. Определяем перемещения точек - границ участков и строим эпюру . Для этого определяем абсолютные деформации участков по закону Гука.

; .

; ;.