Варианты исходных данных

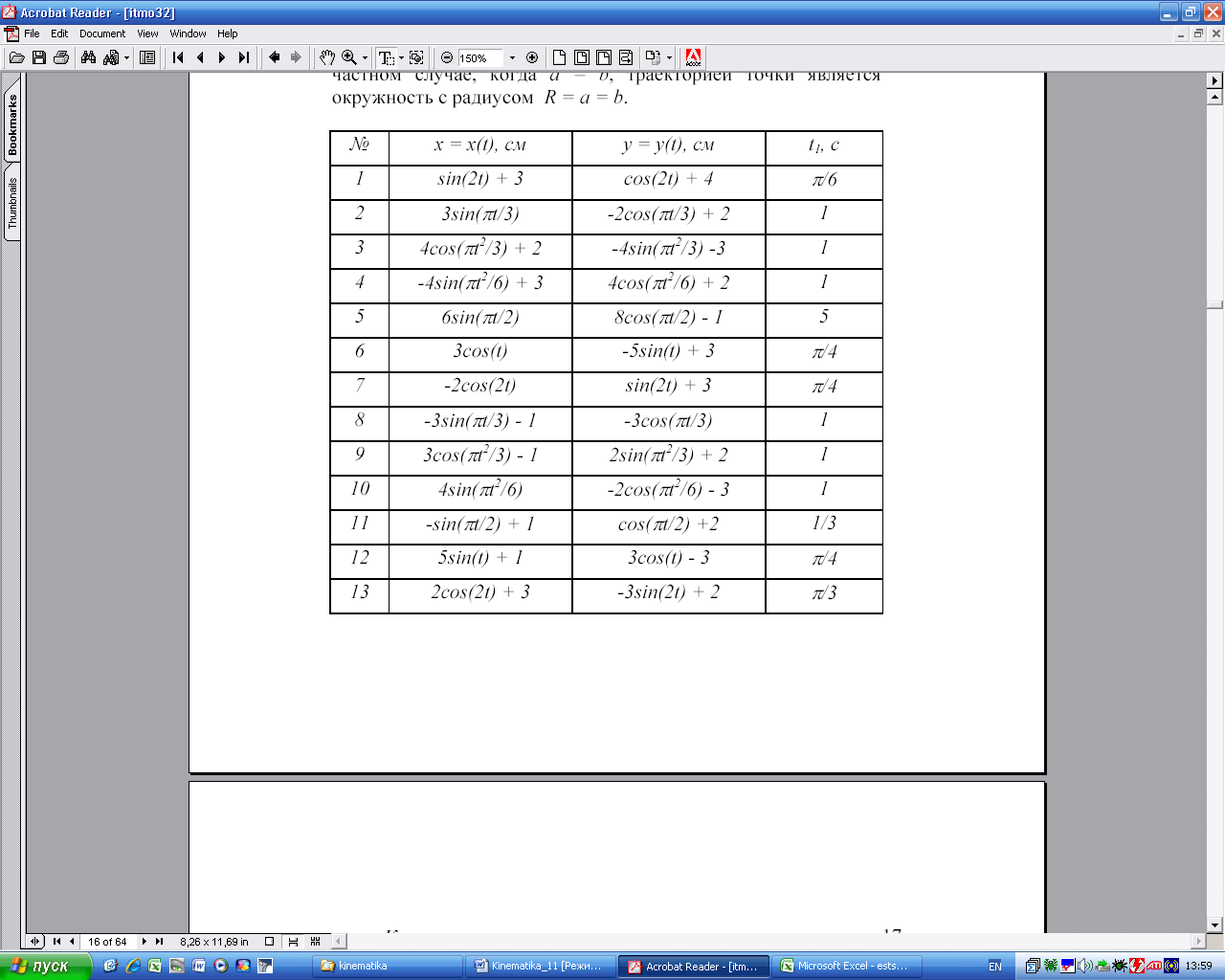
Продолжение табл. 2

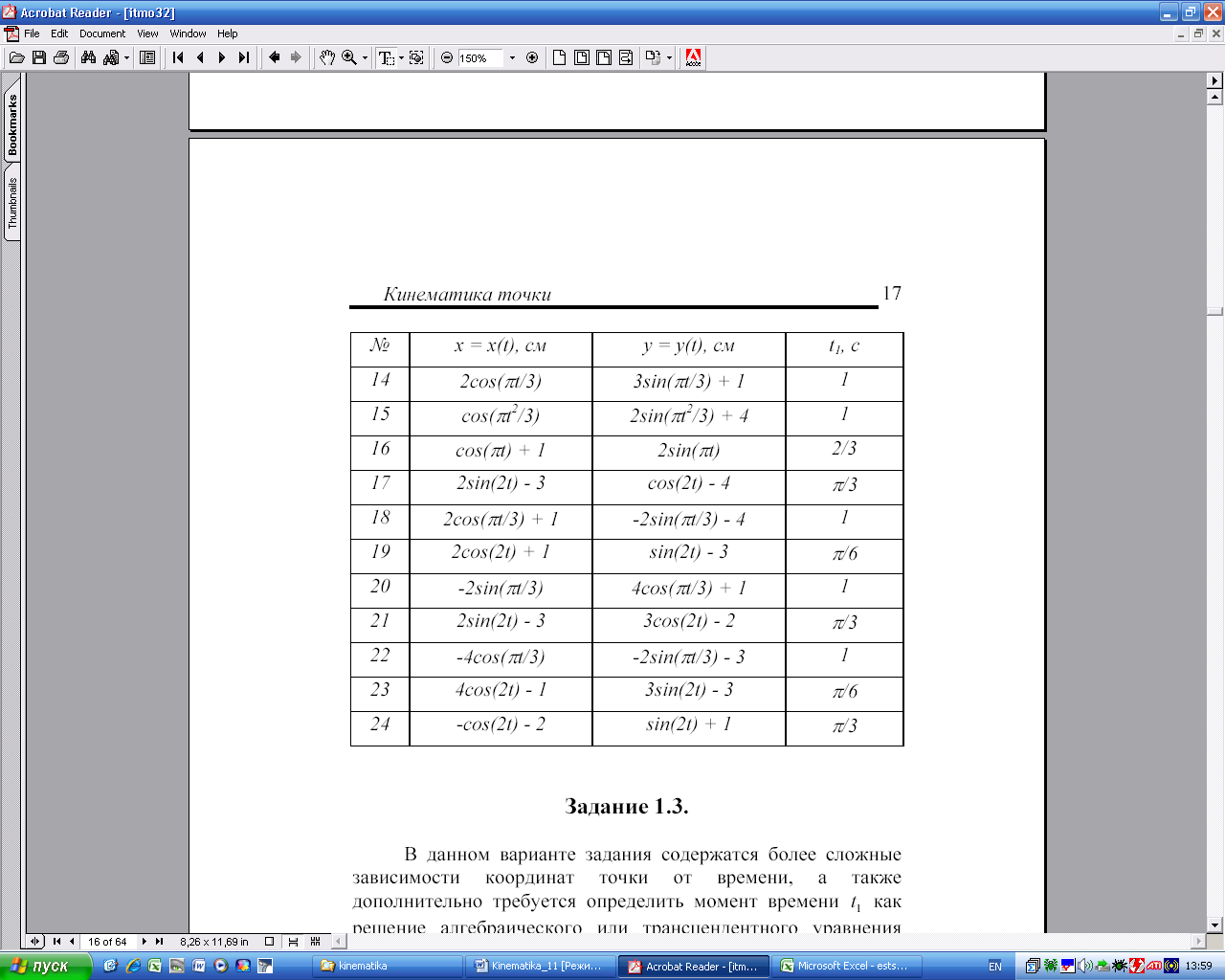
Методические указания

Перед выполнением задания необходимо изучить тему «Кинематика точки». При решении задачи на определение уравнения траектории точки и ее кинематических характеристик целесообразно придерживаться следующего порядка:

1) исключить из уравнений движения точки в координатной форме время и получить уравнение относительно координат точки;

2) построить траекторию точки, указав при этом, является ли траекторией движения точки вся линия или какая-то ее часть;

3) по уравнениям движения точки найти ее координаты, проекции скорости и ускорения на оси координат в данный момент времени, показать на чертеже положение точки и построить векторы скорости и ускорения;

4) определить касательное и нормальное ускорения точки в данный момент времени и показать на чертеже разложение вектора ускорения точки на указанные составляющие;

5) определить по направлениям векторов скорости и касательного ускорения точки, является ли ее движение в данный момент времени ускоренным или замедленным;

6) найти радиус кривизны в соответствующей точке траектории.

В некоторых вариантах при расчетах следует использовать тригонометрические тождества:

1.6. Задания для самостоятельной работы

1.6.1. Ускорение точки при векторном способе задания движения

Пример. Движение материальной точкиМзадано уравнением.

Ускорение точки направлено … (выберите один правильный ответ из списка предложенных):

• перпендикулярно оси Оx

• параллельно оси Оx

• параллельно плоскости yОz

• параллельно оси Оz

Решение. Ускорение точки определяется следующим образом:

, в данном случае:

, или .

Т.к. , то,,.

Ответ: Полное ускорение точки параллельно осиОх.

Возможны и другие варианты ответов, например, полное ускорение точки направлено:

• перпендикулярно оси Оу;

• перпендикулярно оси Оz;

• параллельно плоскости xOy;

• параллельно плоскости xOz;

• перпендикулярно плоскости yOz.

Самостоятельно решите следующие тестовые задания (табл. 3).

Условие: Движение материальной точкиМзадано уравнением. Ускорение точки направлено … (выберите один правильный ответ из списка предложенных).

Таблица 3

Варианты тестовых заданий на тему: "Ускорение точки при векторном способе задания движения"

№		Варианты ответов
1		перпендикулярно плоскости xОz (не параллельно осям) перпендикулярно плоскости yОz перпендикулярно оси Оx параллельно оси Оx
2		параллельно оси Оx параллельно плоскости xОy перпендикулярно оси Оz параллельно оси Оz
3		перпендикулярно плоскости xОz перпендикулярно оси Оy параллельно плоскости xОy (не параллельно осям) параллельно плоскости xОz
4		перпендикулярно плоскости xОz перпендикулярно оси Оy параллельно плоскости xОz (не параллельно осям) параллельно оси Оy

1.6.2. Ускорение точки при координатном способе задания движения

Пример. Точка движется согласно уравнениям,(x,y– в метрах). Модуль ускорения точки (в м/с²) равен… (выберите один правильный ответ из списка предложенных): 0; 6; 12; 3.

Решение. Модуль ускорения точки при координатном способе задания движения точки определяется следующим образом:

.

Где - проекции вектора ускорения точки на координатные оси, которые вычислим:

(м/с²),(м/с²),(м/с²).

Модуль полного ускорения точки равен:

(м/с²).

Ответ:а= 6 м/с².