5.9. Задания для самостоятельной работы

5.9.1 Скорости точки при сложном движении

Пример. В кривошипно-кулисном механизме (табл. 23 схема 1) кривошипOА длиной 10 (см) вращается с угловой скоростью=6 (рад/с). Определите относительную скорость ползуна Ав тот момент, когда угол φ=120º.

Рис. 70. Определение относительной скорости ползуна

Решение. Для решения данной задачи необходимо сначала изобразить исследуемый механизм в заданном положении (рис. 70). На схеме точкаА ползуна совершает сложное движение, свяжем кулисуKLMс подвижной системой отсчета. Тогда в относительном движении точкаА перемещается вдоль кулисы по участкуKL(вектордолжен быть направлен вдоль этой траектории). В переносном движении перемещение той точки кулисы, с которой совпадает исследуемая точкаА, будет ограничено горизонтальными направляющими (вектордолжен быть параллелен этим направляющим). Очевидно, что в абсолютном движении точкаАбудет вращаться вместе с кривошипомOA(вектордолжен быть перпендикулярен звенуОАи сонаправлен с угловой скоростью кривошипа ω). Зная траектории точкиАв относительном, переносном и абсолютном движении и определенно зная направление вектора, согласно теореме о сложении скоростей, построим параллелограмм скоростей. Спроецировав векторное равенствона вертикальную ось, получим:

, отсюда, т.к. ,(см/с).

Ответ:см/с.

Самостоятельно решите следующие тестовые задания (табл. 23)

Условие: В кривошипно-кулисном механизме кривошипOА (ОМ)вращается с угловой скоростью. Для заданного положения механизма (табл. 23) определите относительную скоростьползуна А (обозначена) иликулисы АВ(обозначена) … (выберите один правильный ответ из списка предложенных).

Таблица 23

Варианты заданий по теме «Скорости точки при сложном движении»

№	Схема	Варианты ответов
1	OА=10 (см), =6 (c-1), =30°
2	OМ=10 (см), =2 (c-1), =30°
3	OМ=20 (см), =1 (c-1), =45°

5.9.2. Направление ускорения Кориолиса

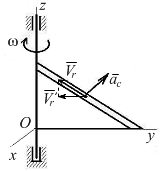
Пример. Пластина вращается  вокруг оси Оz, проходящей через вертикальный катет треугольной пластины с угловой скоростью ω (рис. 71). По прямолинейному каналу на пластине движется точка с относительной скоростью V_r. Ускорение Кориолиса направлено НЕВЕРНО  на схеме…

1. 2.

3. 4.

Рис. 71. Определение направления ускорения Кориолиса

Решение. Во всех представленных случаях вектор будет лежать на осиOz, соответственно плоскость, перпендикулярная этому вектору – плоскость Oxy. Окружность, описываемая той точкой пластины, с которой совпадает исследуемая точка, будет находиться в этой плоскости. Для определения направления ускорения Кориолиса используем правило Жуковского. Проекция вектора относительной скоростина плоскость, перпендикулярную, совпадет с нормалью, проходящей через исследуемую точку и центр описываемой окружности (в данном случае||Oy). Направление вектора получим, повернувна угол 90º в сторону вращения(||Ox и совпадает с касательной к окружности). Таким образом, ускорение Кориолиса направлено неверно на схеме 4.

Самостоятельно решите следующие тестовые задания (табл. 24)

Условие: Пластина вращается с угловой скоростью ω вокруг оси. В вариантах 1-3 ось вращения проходит через центр пластины, в варианте 4 – вдоль горизонтального катета треугольной пластины (табл. 24). По прямолинейному каналу на пластине движется точка с относительной скоростью V_r. Ускорение Кориолиса направлено НЕВЕРНО  на рисунке… (выберите один вариант ответа из списка предложенных).

Таблица 24