5.7. Примеры выполнения расчетно-графической работы по теме «Сложное движение точки»

5.7.1. Пример 1

Условие: Квадратная пластина вращается вокруг оси, проходящей через точкуОперпендикулярно плоскости пластины, по закону(рад) (положительное направление отсчета угла φ показано на рис. 68 дуговой стрелкой). По диагонали пластины движется точка М по закону, положительное направление отсчетаs– отАкD. расстояние от вершины квадратаBдо оси вращенияOравно. Сторона квадрата равна. Определить абсолютную скорость и абсолютное ускорение точкиМдля момента времениt₁=1(с).

Дано: , (рад),.

Найти: ,приt₁=1 (с).

Рис. 68. Расчетная схема к примеру 1

Решение. Рассматрим движение точки М как сложное, считая ее движение по диагонали квадрата относительным, а вращение пластины вместе с исследуемой точкой – переносным.

1. Относительное движение. Это движение происходит по закону .

Определим положение точки M в момент времени :

(см).

Знак «минус» говорит о том, что точка М в момент находится по другую сторону от точкиА на диагонали прямоугольной пластины.

Определим и точки М по формулам:

.

(см/с).

(см/с²).

Знаки показывают, что вектор направлен в сторону положительного отсчета расстояния s, а вектор – в противоположную сторону. Изобразим эти векторы на рис. 68.

2. Переносное движение. Это движение происходит по закону: (рад).

Найдем угловую скорость ω и угловое ускорение ε переносного вращения:

; при (рад/с);(рад/с²).

Знаки указывают, что при направление ω и ε совпадают с направлением положительного отсчета угла φ; покажем это на рис. 68.

Для определения и определим расстояние M₁О от точки M₁ до оси вращения. Из рис. 68 видно, что:

,

где AM₁ = s₁ = 48 (см), (см).

Тогда (см).

В момент времени получим:

(см/с);

(см/с²); (см/с²).

Изобразим на рис. 68 векторы ,с учетом направления ω и ε, векторнаправляем к оси вращения вдоль отрезкаM₁О.

3. Ускорение Кориолиса. Модуль этого ускорения определяется по формуле: , где α – угол между векторамии. В данном случае этот угол равен 90º, т.к. ось вращения перпендикулярна плоскости пластины, в которой расположен вектор. Численно в момент времени, когда(см/с) и(рад/с), получим:

(см/с²).

Направление найдем по правилу Жуковского: т.к. вектор лежит в плоскости, перпендикулярной оси вращения, то повернем его на 90º в направлении ω, т.е. по ходу часовой стрелки. Изобразим вектор на рис. 68. Иначе направление можно найти, учтя, что .

4. Определение абсолютной скорости . Проведем координатные осиM₁xy (рис. 68) и спроецируем обе части векторного равенства на эти оси. Получим для момента времени :

(см/с);

(см/с).

Тогда (см/с).

Учитывая, что в данном случае угол между иравен 135º, значениеможно также определить по теореме косинусов:

(см/с)

5. Определим абсолютное ускорение . По теореме о сложении ускорений:.

Для определения спроецируем обе части данного векторного равенства на проведенные осиM₁xy, получим:

(см/с²);

(см/с²);

Находим значение абсолютного ускорения:

(см/с²).

Ответ: см/с, см/с².

5.7.2. Пример 2

У

Рис. 69. Расчетная схема к примеру 2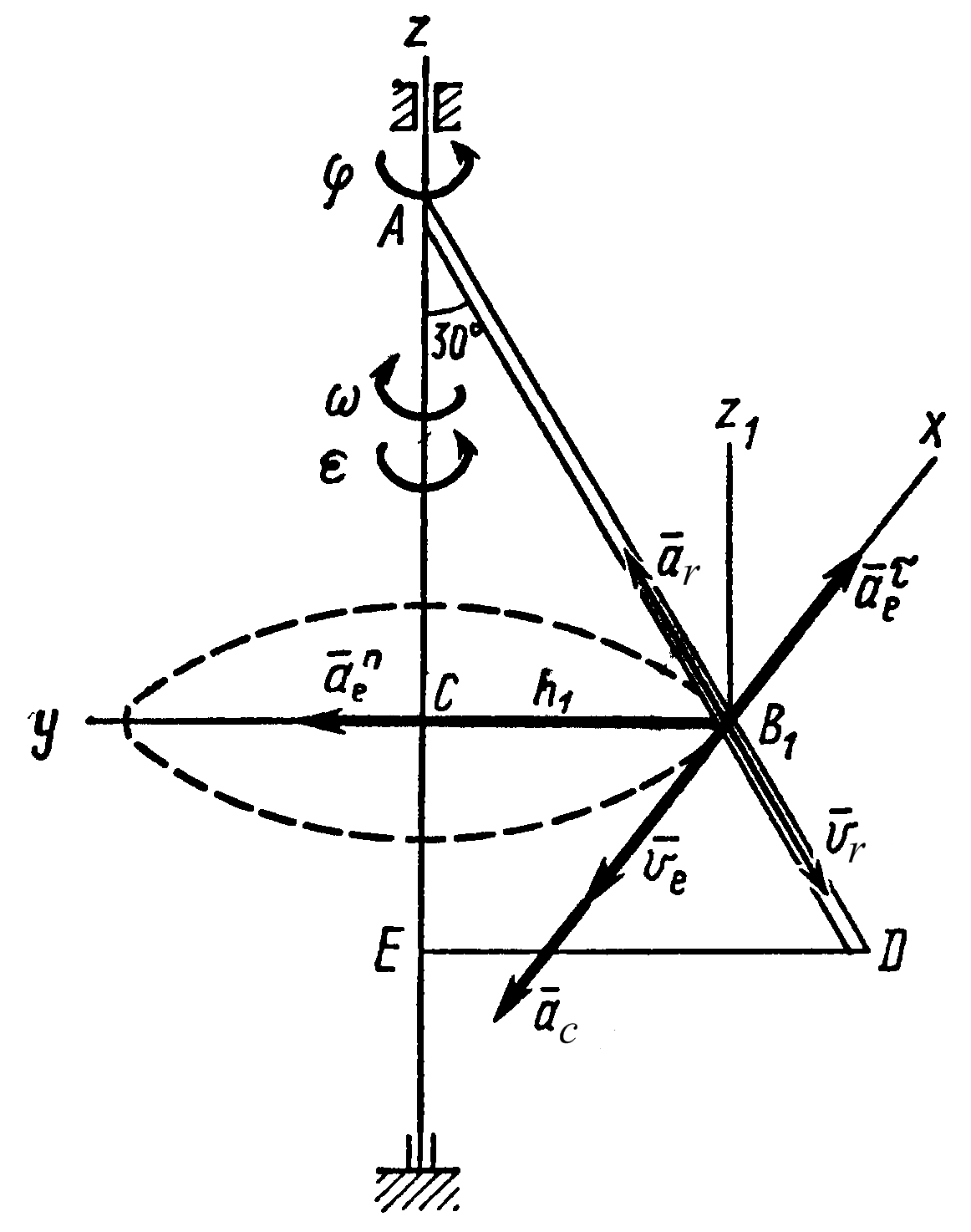

словие: Треугольная пластина ADE вращается вокруг оси z по закону φ = f₁(t) (положительное направление отсчета угла φ показано на рис. 69 дуговой стрелкой). По гипотенузе AD движется точка В по закону s = =АВ=f₂(t); положительное направление отсчета s – от А к D.

Дано: ,(φ – в радианах,s – в сантиметрах, t — в секундах).

Найти: абсолютную скорость и абсолютное ускорениев момент времениt₁=2 с.

Решение. Рассмотрим движение точки B как сложное, считая ее движение по прямой AD относительным, а вращение пластины – переносным. Тогда абсолютная скорость и абсолютное ускорениенайдутся по формулам:

, ,

где .

Определим все входящие в данные равенства величины.

1. Относительное движение. Это движение прямолинейное и происходит по закону:

.

Поэтому

, .

В момент времени t₁ = 2 с имеем

см, см/с,см/с².

Знаки показывают, что вектор направлен в сторону положительного отсчета расстояния s, а вектор – в противоположную сторону. Изображаем эти векторы на рис. 69.

2. Переносное движение. Это движение (вращение) происходит по закону .

Найдем угловую скорость ω и угловое ускорение ε переносного вращения:

; и приt₁ = 2 с,

с^-1; с^-2.

Знаки указывают, что в момент t₁ = 2 с направление ε совпадает с направлением положительного отсчета угла φ, а направление ω ему противоположно; отметим это на рис. 69 соответствующими дуговыми стрелками.

Из рисунка находим расстояние h₁ точки В₁ от оси вращения z:

см. Тогда в момент t₁ = 2 с получим:

см/с,

см/с², см/с².

Изобразим на рис. 69 векторы и (с учетом знаков ω и ε) и ; направлены векторы и перпендикулярно плоскости ADE, а вектор – по линии В₁С к оси вращения.

3. Ускорение Кориолиса. Так как угол между вектором и осью вращения (вектором ) равен 30°, то численно в момент времени t₁ = 2 с

см/с².

Направление найдем по правилу Жуковского. Для этого вектор спроецируем на плоскость, перпендикулярную оси вращения (проекция направлена противоположно вектору ) и затем эту проекцию повернем на 90° в сторону ω, т. е. по ходу часовой стрелки; получим направление вектора . Он направлен перпендикулярно плоскости пластины так же, как вектор (см. рис. 69).

4. Определение абсолютной скорости . Так как, а векторы и взаимно перпендикулярны, то в момент времениt₁ = 2 с м/с.

5. Определение абсолютного ускорения . По теореме о сложении ускорений

.

Для определения проведем координатные осиB₁xyz₁ и вычислим проекции на эти оси. Учтем при этом, что векторы и лежат на оси х, а векторы и расположены в плоскости B₁yz₁, т. е. в плоскости пластины. Тогда, проецируя обе части векторного равенства на оси B₁xyz₁, получим для момента времени t₁ = 2 с:

см/с²,

см/с²,

см/с².

Отсюда находим значение

см/с².

Ответ: м/с,см/с².