4.4. Общий случай движения свободного твердого тела

Рассмотрим наиболее общий случай движения твердого тела, когда оно является свободным и может перемещаться как угодно по отношению к системе отсчета Ох₁у₁z₁ (рис. 58). Установим вид уравнений, определяющих закон рассматриваемого движения. Выберем произвольную точку А тела в качестве полюса и проведем через нее оси , которые при движении тела будут переме­щаться вместе с полюсом поступательно. Тогда положение тела в системе отсчета будет известно, если будем знать положение полюса А, т.е. его координаты х_1А, у_1А, z_1А, и положение тела по отношению к осям , определяемое, как и в случае движения твердого тела, имеющего одну неподвижную точку, углами Эйлера φ, ψ, θ (см. рис. 54). На рис. 58 углы Эйлера не показаны, чтобы не затемнять чертеж. Следовательно, уравнения движения свободного твердого тела, позволяющие найти его положение по отношению к системе отсчета в любой мо­мент времени, имеют вид:

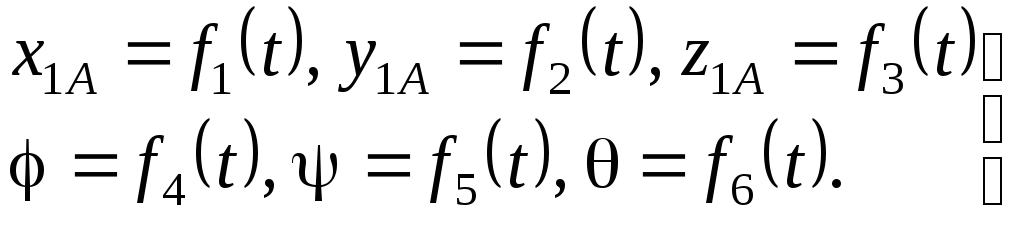
Рис. 58. Определение уравнений движения свободного твердого тела	Рис. 59. Схематичное представление свободного движения твердого тела

Установим теперь геометрическую картину рассматриваемого движения. Первые три из представленных уравнений опре­деляют то движение, которое тело совершало бы при постоянных углах φ, ψ, θ, т. е. при поступательном движении тела вместе с полюсом А. Последние же три уравнения определяют движение, которое происходило бы при постоянных значениях координат х_1А, у_1А, z_1А, т. е. когда точка А неподвижна. Но движение тела вокруг неподвижной точки слагается из поворотов вокруг мгновенных осей вращения. Отсюда заключаем, что в общем случае движение свободного твердого тела можно рассматривать как слагающееся из поступательного движения, при котором все точки тела движутся как произвольно выбранный полюс А со скоростью , и из серии элементарных поворотов с угловой скоростью вокруг мгновенных осей вращения, проходящих через полюс А (рис. 59). Такой будет, например, кар­тина движения любого непоступательно перемещающегося в воз­духе тела: брошенного камня, самолета, проделывающего фигуры высшего пилотажа, артиллерийского снаряда и т. д.

Основными кинематическими характеристиками движения яв­ляются скорость и ускорение полюса A, определяющие скорость и ускорение поступательной части движения, а также угловая скорость и угловое ускорение вращения вокруг полюса. Зна­чения этих величин в любой момент времени можно найти по ура­внениям движения свободного твердого тела. Заметим, что если за полюс принять другую точку тела, например, точку В (см. рис. 58), то значения и окажутся отличными от и (предполагается, что тело движется не посту­пательно). Но если связанные с телом оси, проведенные из точки В (на рис. 58 не показаны), направить так же, как и в точке А, то значения углов φ, ψ, θ, а следовательно, и связанные с ними уравнения движения не изменятся. Поэтому здесь, как и в случае плоского движения, вращательная часть движения тела, в частности значения ω и ε, от выбора полюса не зависят.

Движение свободного твердого тела может быть, в частном случае, плоскопараллельным.

Скорости и ускорения точек тела. Скорость любой точки М тела в рассматриваемом движении слагается, как и в случае плоскопараллельного движения, из скорости полюса А и скорости , которую точка М получает при движении вместе с телом вокруг полюса А. При этом, так как движение тела вокруг полюса А происходит как движение вокруг неподвижной точки, то значение определяется формулой , где, т. е. .

Таким образом,

, или .

Аналогично, вектор ускорения любой точки М тела:

,