2.6. Задания для самостоятельной работы

2.6.1. Скорости точек при передаче движения

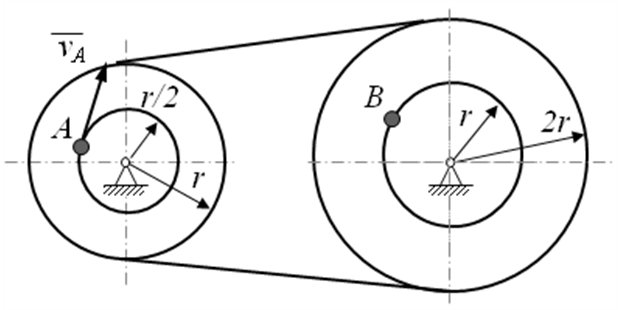
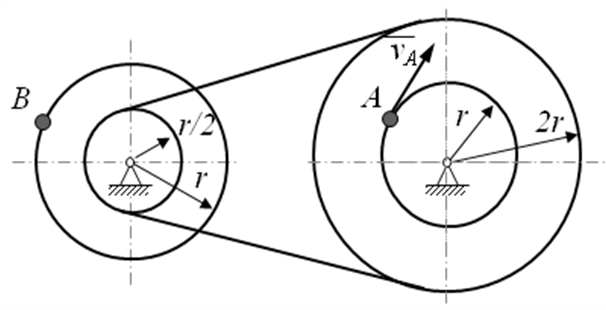
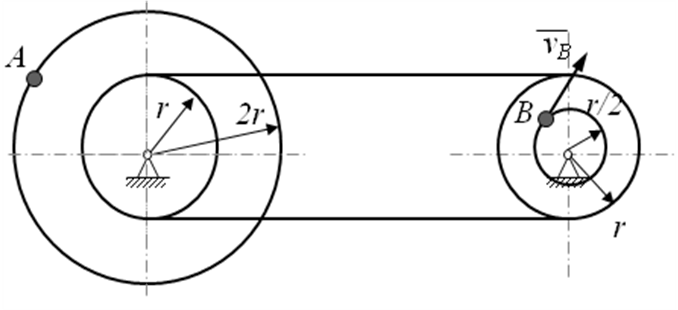
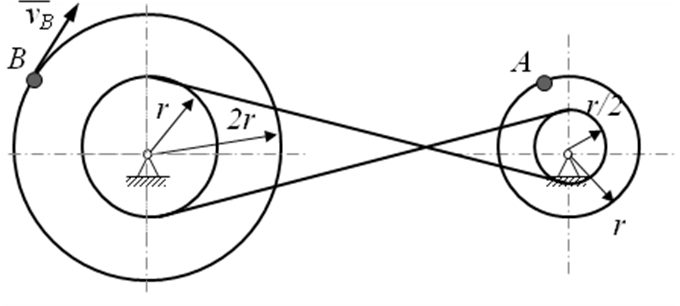
В предлагаемой таблице 8 для вариантов 1-4 известна скорость точки одного из шкивов, тогда скорость обозначенной точки другого шкива в этом случае равна … (выберите один правильный ответ из списка предложенных).

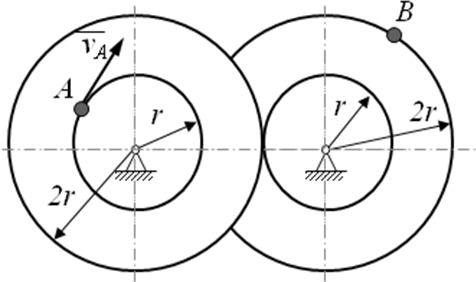
Для варианта 5 известна скорость точки Аодного из колес, тогда скорость точкиВдругого ступенчатого колеса равна … (выберите один правильный ответ из списка предложенных).

Таблица 8

Варианты тестовых заданий по теме «Скорости точек при передаче движения»

№	Расчетная схема	Заданная скорость точки	Варианты ответов
1		VA=8 см/с	VB=8 см/с VB=4 см/с VB=16 см/с VB=2 см/с
2		VA=8 см/с	VB=16 см/с VB=8 см/с VB=4 см/с VB=32 см/с
3		VB=12 см/с	VА=3 см/с VА=48 см/с VА=24 см/с VА=6 см/с

Продолжение табл. 8

4		VB=30 см/с	VА=15 см/с VА=120см/с VА=60 см/с VА=30 см/с
5		VA=20 см/с	VB=10 см/с VB=20 см/с VB=80 см/с VB=40 см/с

2.6.2. Скорости и ускорения точек вращающегося тела

Пример 1: Диск радиусаR=10 см вращается вокруг осиОх(рис. 26) по закону (- в рад,t- в сек). Скорость точкиАприt=2c будет равна … (выберите один правильный ответ из списка предложенных):

Рис. 26. Иллюстрация к примерам 1-3

70 см/с 23 см/с 20 см/с 40 см/с

  Решение. Скорость точкиАпо модулю равна:

, где (рад/с).

Ответ:

Пример 2: Диск радиусаR=10 см вращается вокруг осиОхпо закону (- в рад,t- в сек). Касательное ускорение точкиАв момент времениt = 3c  равно… (выберите один правильный ответ из списка предложенных):

• 40 см/с²

• 90 см/с²

• 20 см/с²

• 120 см/с²

Решение: Касательное ускорение точкиАпо модулю равно:

, где (рад/с²).

Ответ: .

Пример 3: Диск радиусаR=10 см вращается вокруг осиОхпо закону (- в рад,t- в сек). Ускорение точкиАприt=1c равно … (выберите один правильный ответ из списка предложенных):

• 0 см/с²

• 0 см/с²

• 50 см/с²

• 250 см/с²

Решение. Модуль полного ускоренеия точки А равен:

.

Ответ: .

2.6.3. Угловые характеристики вращательного движения тела

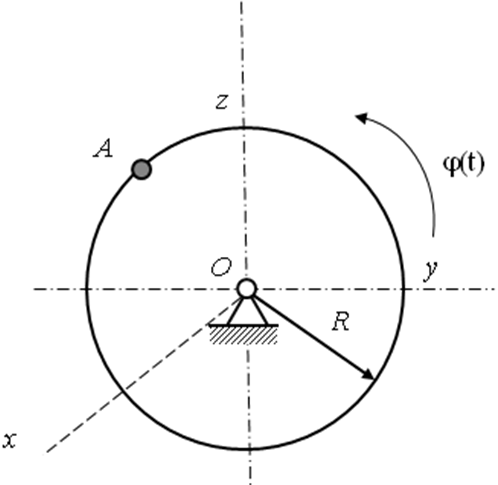
Пример 4. Круглая пластинка вращается вокруг оси, проходящей через точкуО,  перпендикулярной плоскости пластины с угловой скоростью(рис. 27). Укажите точку с максимальной линейной скоростью … (выберите один правильный ответ из списка предложенных):

Рис. 27. Иллюстрация к примеру 4

В А D С

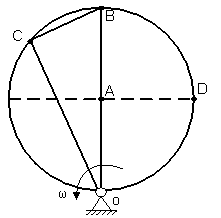
Решение: Чем дальше точка отстоит от оси вращения, тем больше модуль ее линейной скорости. Для решения задачи необходимо найти точку, максимально удаленную от точкиО, через которую проходит ось вращения. В данном примереОВ>ОС>OD>ОА, следовательно, точка с максимальной скоростью – это точкаВ.

Пример 5.Круглая пластинка вращается вокруг оси, проходящей через точкуО,  перпендикулярной плоскости пластины с угловым ускорением ε (см. рис. 28).

Укажите точку с наибольшим касательным ускорением … (выберите один правильный ответ из списка предложенных):

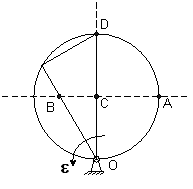
Рис. 28. Иллюстрация к примеру 5

В А D С

Решение: Чем дальше точка отстоит от оси вращения, тем больше модуль ее касательного ускорения. Для решения задачи необходимо найти точку, максимально удаленную от точкиО, через которую проходит ось вращения. В данном примереОD>ОA>OB>ОC, следовательно, точка с максимальным касательным ускорением – это точкаD.

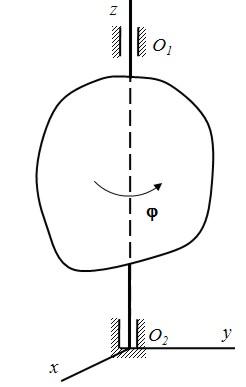
Пример 6. Твердое тело вращается вокруг неподвижной оси О₁О₂ (см. рис. 29) по закону . В момент времени  t = 1 c  тело будет вращаться … (выберите один правильный ответ из списка предложенных):

Рис. 29. Иллюстрация к примерам 6-8

замедленно равнозамедленно равноускоренно ускоренно равномерно Решение. Угловая скорость твердого тела: . Угловое ускорение твердого тела: .

Угловое ускорение твердого тела равно нулю, твердое тело вращается с постоянной угловой скоростью, движение твердого тела равномерное.

Ответ: равномерное движение.

Пример 7. Твердое тело вращается вокруг неподвижной осиО₁О₂по закону. В момент времениt = 1c  тело будет вращаться … (выберите один правильный ответ из списка предложенных):

• замедленно

• равнозамедленно

• равноускоренно

• ускоренно

• равномерно

Решение. Угловая скорость твердого тела:

. При t = 1(с), .

Угловое ускорение твердого тела: .

Угловая скорость твердого тела в данный момент времени отрицательна. Угловое ускорение твердого тела постоянно, не зависит от времени, положительно. Т.к. знаки угловой скорости и углового ускорения не совпадают, следовательно, движение твердого тела или равнозамедленное, или замедленное. Если при этом угловое ускорение не зависит от времени – движение равнозамедленное, если зависит от времени – то замедленное. В данном примере твердое тело вращается равнозамедленно.

Ответ: равнозамедленное движение.

Пример 8. Твердое тело вращается вокруг неподвижной осиО₁О₂по закону. В момент времениt = 1c  тело будет вращаться … (выберите один правильный ответ из списка предложенных):

• замедленно

• равнозамедленно

• равноускоренно

• ускоренно

• равномерно

Решение. Угловая скорость твердого тела: .

При t = 1(с), .

Угловое ускорение твердого тела:

.

При t = 1(с), .

Знаки угловой скорости и углового ускорения твердого тела в данный момент времени совпадают, угловое ускорение твердого тела является функцией времени, следовательно, вращение твердого тела ускоренное.

Ответ: ускоренное движение.