
vanyashov_a_d_kustikov_g_g_uchebnoe_posobie_dlya_kursovogo_p
.pdf
2.2. Расчет лопатки рабочего колеса на прочность
Рабочие лопатки представляют собой незамкнутую цилиндрическую оболочку переменной ширины с упругоили жесткозащемленными криволинейными краями (приклепанными, приваренными или припаянными к основному и покрывающему дискам) и свободными прямолинейными кромками [23].
На лопатку действуют следующие нагрузки: центробежные силы от собственной массы; силы реакции со стороны основного и покрывающего дисков; перепад давлений на передней и задней сторонах лопатки.
Точно учесть влияние всех перечисленных выше силовых факторов на лопатку в инженерных расчетах достаточно сложно. Поэтому рассмотрим расчет лопатки на прочность при действии на нее только центробежных сил.
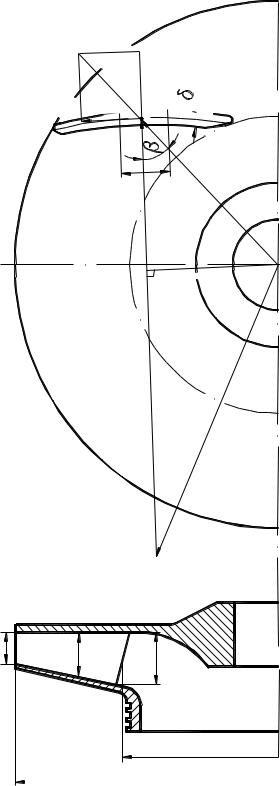
Расчетная схема лопатки при таком случае нагружения представлена на рис. 2.15. Нагрузка от центробежной силы, приходящаяся на единицу длины лопатки, Н/м:
q = ρм δ R l ω2 ,
где ρм – плотность материала лопатки, кг/м3; δ - толщина лопатки, м; R – текущий радиус точки, лежащей на средней линии лопатки, м; l – длина лопатки (l = 1 м); ω – угловая скорость вращения ротора, 1/с.
Нагрузка от центробежной силы действует вдоль радиуса R и может быть разложена на две составляющие (нормальную к поверхности лопатки qn и касательную к поверхности лопатки qt):
q = qn + qt .
Действие касательных сил qt приводит к изгибу лопатки относительно нормали к ее поверхности. Действием этих сил можно пренебречь ввиду значительной жесткости лопатки в этом направлении [23]. В итоге лопатка считается нагруженной только нормальной составляющей центробежных сил. Действие силы qn равносильно изгибу плоской пластины.
Из расчетной схемы следует:
qn = q cos β = ρм δ ω2 R cos β .
Поскольку угол лопатки β и ширина лопатки b меняются по радиусу R , изгибающий момент найдем для среднего сечения лопатки по ее высоте, Н·м:
Миз = |
q |
n |
b2 |
, |
|
24 |
|||
|
|
|
||
Миз = ρм δ ω2 b2 R cos β . 24
Момент сопротивления
W = l δ 2 = δ 2 , т.к. l = 1 м.
6 6
Напряжения в среднем сечении лопатки на некотором радиусе R, Па:
130

σиз = Миз .
W
Чтобы найти значения изгибающего момента по длине лопатки, необходимо установить закон изменения ширины лопатки b и угла β в функции от радиуса R. Для этого воспользуемся расчетной схемой рис. 2.3.
Из треугольника со сторонами x, R, c
R cos β = x .
Высота треугольника c2 = R2 − x2 |
= Rц2 − y2 , откуда |
x2 = R2 + y2 − Rц2 . |
|||||||||||||||
Т.к. y = Rл − x , то можно преобразовать y2 |
= (Rл − x)2 |
= Rл2 −2Rл x + x2 . |
|||||||||||||||
Подставив полученное выражение в предыдущее, получим |
|
||||||||||||||||
|
x2 = R2 + Rл2 − 2Rл x + x2 − Rц2 , |
|
|
|
|||||||||||||
|
|
2Rл x = R 2 + Rл2 − Rц2 . |
|
|
|
|
|
|
|||||||||
Выразим отсюда x: |
|
|
R2 |
+ R |
2 |
− R2 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
x = |
|
|
|
л |
|
|
ц |
. |
|
|
|
|
|
|
|
|
|
|
2Rл |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
R2 + Rл2 − Rц2 |
|
R |
л |
|
|
|
Rц2 |
1 |
|
2 |
|||||
R cos β = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R . |
||
|
2Rл |
|
= |
|
2 |
− |
|
|
+ |
2Rл |
|||||||
|
|
|
|
|
|
|
|
2Rл |
|
|
|||||||
|
R |
|
|
Rц2 |
1 |
|
|
Обозначим К1 = |
|
л |
− |
|
; К2 = |
|
, |
|
|
|
|||||
2 |
|
|
|||||
|
|
2Rл |
2Rл |
||||
тогда
R cos β = К1 + К2 R2 .
Ширина лопатки находится из соотношения
|
|
|
|
|
|
|
|
|
|
|
|
b = К3 − К4 R , |
||
|
К |
|
= b + |
b1 − b2 |
R |
|
К |
|
= |
b1 − b2 |
|
|||
где |
3 |
|
; |
4 |
R − R . |
|||||||||
|
1 |
R |
2 |
− R |
1 |
|
|
|||||||
|
|
|
|
|
1 |
|
|
|
|
|
2 |
1 |
|
|
Таким образом, изгибающий момент в различных сечениях по длине лопатки в функции от радиуса колеса
Миз = ρм δ ω2 (К3 − К4 R)2 (К1 + К2 R2 ) . 24
131
q 

 q
q п
п
 qt
qt 



1=l
x
c
(12)- Rл
|
) |
|
2 |
|
- |
|
1 |
R |
( |
ц |
|
|
y
b2 |
b |
b1 |
1 |
R |
|
|
2 |
R |
|
Рис. 2.15. Расчетная схема к определению изгибающих напряжений в лопатке
132
2.3. Расчет заклепок лопаток на срезывающие напряжения
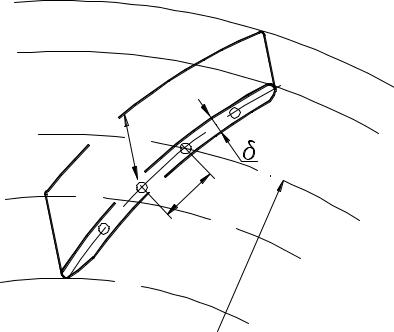
При определении срезывающих напряжений в материале заклепок предполагается, что каждая заклепка нагружена только центробежной силой от элемента лопатки длиной, равной шагу заклепок t (рис. 2.4). В качестве допущения пренебрегают взаимными перемещениями и деформациями основного и покрывающего дисков.
Центробежная сила от элемента лопатки, Н:
Fц / б = ρм b δ t R ω2 .
Напряжения среза в заклепке, МПа:
|
|
τср |
= |
Fц / б |
, |
|
|
|
|||
|
|
|
|
f з |
|
где f з = |
π d 2 |
- площадь сечения заклепки, мм2; dз – диаметр заклепки, мм. |
|||
з |
|||||
|
4 |
|
|
|
|

 b
b

 t
t
R
Рис. 2.16. Расчетная схема к определению срезывающих напряжений в заклепках
133
2.4.Расчет корпусных элементов компрессора
Ккорпусным элементам конструкции центробежного компрессора относится ряд элементов, формирующих его проточную часть, в частности верхняя и нижняя половины корпуса для корпусов с горизонтальным разъемом, корпус и крышки для корпусов с вертикальным разъемом, фланцы для соединения корпусных частей и крышек с корпусом, внутрикорпусные диафрагмы.
Корпус центробежного компрессора представляет собой оболочку сложной формы с ребрами жесткости, фланцами и патрубками. Кроме того, распределение перепада давлений и температур по длине корпуса является неравномерным. В связи с этим определение напряжений в стенках корпуса представляет достаточно трудоемкую задачу. Поэтому при приближенном расчете на прочность корпус (или фрагменты его) рассматривают как тонкостенную или толстостенную оболочку, нагруженную внутренним давлением.
Ниже приводятся методики расчета на прочность корпусных элементов, имеющих простые геометрические формы (цилиндрические элементы корпусов, плоские крышки).
2.4.1.Расчет цилиндрических корпусных элементов, нагруженных внутренним давлением
Поскольку корпуса центробежных компрессоров с горизонтальным разъемом имеют сложные конструктивные формы, получаемые отливкой, то, пользуясь методикой расчета тонкостенных оболочек, можно ориентировочно оценить необходимую толщину стенки для элементов корпуса, имеющих форму цилиндрической оболочки. Корпуса компрессоров с вертикальным разъемом имеют, как правило, цилиндрическую форму, поэтому для расчета толщины стенки используется теория тонкостенных оболочек, если давление сжимаемого газа не превышает 10 МПа. Для корпусов компрессоров высокого давления при расчете толщины стенки пользуются теорией толстостенных оболочек [22, 24, 25]. Расчетная схема цилиндрического корпуса показана на рис. 2.17.
Расчетная толщина стенки
s= max РрD (2 [σ] − Рр )
рРи D (2 [σ]и − Ри ) ,
где D – внутренний диаметр корпуса; Рр – расчетное давление, МПа; Ри – максимальное избыточное давление, создаваемое при испытаниях [24]; [σ] – допускаемое напряжение для материала корпуса при рабочей температуре, МПа; [σ]и - допускаемое напряжение для испытаний.
134

Расчетное давление в большинстве случаев принимается равным максимальному избыточному давлению в корпусе, т.е. конечному давлению компрессора Рр=Рк. Для литых корпусов, если Рк ≤ 0,2 МПа, Рр=0,2 МПа [22].
Давление испытаний:
− для литых корпусов независимо от давления
Pи = max{1,5Рр ([σ]20  [σ]); 0,3};
[σ]); 0,3};
− для нелитых корпусных элементов при Рр < 0,5 МПа
Pи = max{1,5Рр ([σ]20 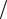 [σ]); 0,2};
[σ]); 0,2};
− для нелитых корпусных элементов при Рр ≥ 0,5 МПа
Pи = max{1,25 Рр ([σ]20  [σ]); (Рр +0,3)}.
[σ]); (Рр +0,3)}.
Допускаемые напряжения в рабочем состоянии для материала корпуса определяются по справочным данным о свойствах материалов, в зависимости от температуры (средней температуры в процессе сжатия) по формуле
[σ ] =η min{σт n т ; σ в nв}, |
(2.4) |
где σт , σв – минимальные значения пределов текучести и прочности при расчетной температуре [26] (табл. 2.2); пт, пв - коэффициенты запаса прочности по пределам текучести пт =1,5 и прочности пв = 2,4.
Допускаемые напряжения [σ]20 для материала корпуса определяются по формуле (2.4) для температуры 20 °С. Значения поправочного коэффициента для отливок η = 0,7 - 0,8.
Допускаемые напряжения для испытаний
[σ ]и =σ т20  nт ,
nт ,
где для гидравлических испытаний коэффициент запаса прочности nт = 1,1; для пневматических испытаний nт = 1,2; σТ20 – предел текучести при температуре 20 °С; МПа берется из справочных данных [24, 26].
Исполнительная (фактическая) толщина стенки корпуса определяется за счет увеличения расчетной толщины стенки на величину технологической прибавки с, которая назначается конструктивно:
s = sр + c .
Полученная толщина стенки должна удовлетворять условию
(s −c) / D ≤ 0,1, |
(2.5) |
при котором цилиндрический корпус считается тонкостенной оболочкой. В этом случае расчетные формулы применены корректно.
Если толщина стенки корпуса известна и она соответствует условию (2.5), то выполняется поверочный расчет, заключающийся в определении допускаемого давления внутри корпуса.
Допускаемое давление в рабочем состоянии
[P] = 2 ϕ [σ] (s −c).
D + s −c
135

|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2.2 |
|
Механические свойства материалов корпусных элементов |
|
||||||||||
|
|
|
|
|
|
Марка стали |
|
|
|
|
|
|
t, °C |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
09Г2С; 16ГС |
|
|
||
|
|
ВСт3 |
10 |
|
20; 20К |
|
12ХМ; 12МХ |
|||||
|
|
|
|
|
|
|
|
σ Т , МПа |
|
|
|
|
|
|
Минимальное |
значение |
предела текучести |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
280 |
|
|
|
20 |
210 |
|
195 |
220 |
|
|
|
|
220 |
|||
|
|
|
|
|
|
|
|
|
240 |
|
|
|
100 |
201 |
|
188 |
213 |
|
|
|
|
219 |
|||
|
|
|
|
|
|
|
|
|
231 |
|
|
|
150 |
197 |
|
183 |
209 |
|
|
|
|
218 |
|||
|
|
|
|
|
|
|
|
|
222 |
|
|
|
200 |
189 |
|
177 |
204 |
|
|
|
|
217,5 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Расчетное |
значение предела прочности σ В |
, МПа |
|
|||||||
|
|
|
|
|
|
|
|
|
470 |
|
|
|
20 |
460 |
|
340 |
410 |
|
|
|
|
450 |
|||
|
|
|
|
|
|
|
|
|
425 |
|
|
|
100 |
435 |
|
310 |
380 |
|
|
|
|
440 |
|||
|
|
|
|
|
|
|
|
|
430 |
|
|
|
150 |
460 |
|
340 |
425 |
|
|
|
|
434 |
|||
|
|
|
|
|
|
|
|
|
439 |
|
|
|
200 |
505 |
|
382 |
460 |
|
|
|
|
430 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Марка чугуна |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
СЧ 12-28 |
|
СЧ 15-32 |
|
СЧ 18-36 |
|
СЧ 21-40 |
|
С15, С17 |
|
МФ-15 |
||
|
|
|
|
|
|
|
|
|||||
|
|
Минимальное |
значение предела текучести σ Т , МПа |
|
||||||||
120 |
|
150 |
|
180 |
|
210 |
|
|
600 |
|
|
600 |
|
|
|
|
|
|
|
|
|
||||
|
|
Расчетное |
значение предела прочности σ В |
, МПа |
|
|||||||
280 |
|
320 |
|
360 |
|
400 |
|
|
170 |
|
|
140 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Pp |
D |
S |
Рис. 2.17. Расчетная схема цилиндрического корпуса
136

Допускаемое давление при испытаниях
[P]и = 2 ϕ [σ+]и −(s −c).
D s c
Расчетное давление не должно превышать допускаемое:
Рр ≤[P] и Ри ≤[P]и .
Если толщина стенки не удовлетворяет условию (2.5), то оболочка считается толстостенной, толщина стенки для нее рассчитывается в следующем порядке.
Расчетная толщина стенки корпуса
sр = 0,5 D (βр −1) ,
где βр – расчетный коэффициент толстостенности, ln βр = [Pσр] .
Исполнительный коэффициент толстостенности
β = D + 2 s D +2 c .
Допускаемое рабочее давление
[P] =[σ] lg β .
2.4.2. Расчет плоских крышек
Расчетная толщина стенки
|
К Ко |
Dр |
|
Рр |
||
|
||||||
sп. р = max |
К К |
|
D |
|
|
Р |
|
о |
р |
||||
|
|
|
|
и |
||
sп = sп. р + c .
Допускаемое давление в рабочем состоянии
[P] = К sКп −о cDр 2 [σ] .
Допускаемое давление при испытаниях
[P]и = К sКп −о cDр 2 [σ]и ,
|
|
|
|
[σ] |
|
|
|
[σ] |
|
, |
(2.6) |
|
|||
|
и |
|
|
(2.7)
(2.8)
где Dр - расчетный диаметр плоской крышки (табл. 2.3); К - коэффициент, учитывающий тип закрепления крышки с фланцем корпуса (табл. 2.3); Ко – коэффициент ослабления, определяемый в зависимости от характера расположения отверстий в крышке [22, 24].
137

Таблица 2.3 Коэффициент К и расчетный диаметр Dр плоских днищ и крышек [22]
Тип |
Эскиз соединения |
|
a |
1 |
Sn |
|
|
S |
D |
|
a  2
2 
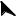
Sn
S D
Условие Dp К
a >1,7 S |
Dp=D |
0,53 |
a >0,85 S |
Dp=D |
0,50 |
a < 0,85 S |
|
0,41 |
3 |
|
Sn |
Sn |
|
|
D |
D |
|
|
S |
|
|
|
S |
|
|
|
|
|
|
|
Sn |
|
4 |
S |
D |
|
|
|
|
|
Dб |
5 |
Sn |
|
|
(s −c) |
|
|
|
|
Dp=D |
0,45 |
|
(sп −с)< 0,25 |
||||||||
|
|
|||||||
|
(s −c) |
≥ 0,25 |
|
0,41 |
||||
(sп −с) |
|
|
||||||
|
(s − c) |
|
|
< 0,5 |
Dp=D |
0,41 |
||
|
(sп − с) |
|
||||||
|
|
|
|
|||||
|
(s − c) |
|
|
|
|
0,38 |
||
|
(sп − с) ≥ 0,5 |
|
||||||
|
|
|
||||||
|
|
|
|
|
|
Dp=Dб |
0,40 |
|
В случае одного отверстия диаметром d в крышке для выхода конца вала коэффициент Ко определяется по формуле
Ко =  1+ d Dр + (d Dр )2 .
1+ d Dр + (d Dр )2 .
Для двух и более отверстий при Σdi < 0,7 Dр
Ко = |
1 − Σ(di / Dр )3 |
1 − Σ(di / Dр ) , |
138

где Σdi - максимальная сумма длин хорд отверстий в наиболее ослабленном диаметральном сечении днища или крышки, определяемая, например, по схеме (рис. 2.18). В этом случае отверстия болтов в расчет не принимают.
Условия применимости формул (2.6)-(2.8): (sп −c) / Dр ≤ 0,11. При
невыполнении этого условия значение допускаемого давления, рассчитанного по формулам (2.7), (2.8), следует умножить на поправочный коэффициент:
Кp = |
2,2 |
. |
|
1+ (6 (sп −c) Dр )2 |
|||
1+ |
|
При расчетном давлении внутри корпуса Рр ≥ 10 МПа расчет плоской крышки ведут как для аппаратов высокого давления.
Расчетная толщина плоской крышки определяется из условия прочности на изгиб диаметрального сечения крышки, наиболее ослабленного отверстиями [22]:
sп. р = 0,45 |
3,8 F (D − D ) + Р |
|
D3 |
, |
|
(Da −2 |
б ср |
р |
ср |
||
|
dо.ш −∑di ) [σ] |
|
|||
где F – расчетное осевое усилие от действующих на крышку нагрузок; Dб – диаметр болтовой окружности или окружности центров шпилек; Dср – средний диаметр уплотнительной поверхности; Dа – наружный диаметр крышки; dо.ш – диаметр отверстия под крепежную шпильку (рис. 2.19); Σdi – максимальная сумма длин хорд отверстий в наиболее ослабленном диаметральном сечении крышки (рис. 2.18).
Диаметр отверстия под крепежную шпильку обычно принимается равным наружному диаметру резьбы шпильки dр.
Наружный диаметр крышки определяется конструктивно из условия
Da ≥ Dб + 2 d р .
Расчетное осевое усилие
F = Fр + Rп .
Равнодействующая внутреннего давления Рр на крышку
Fр =πDср2 Рр 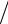 4 .
4 .
Реакция прокладки
Rп =πDсрbσсм ,
где b – исполнительная ширина прокладки; σсм – напряжение смятия прокладки (табл. 2.4).
Средний диаметр уплотнительной поверхности
Dср = D1 +b ,
где D1 – внутренний диаметр плоской металлической прокладки:
D1 = (1−1,03) D .
139
