Basic_Electrical_Engineering_4th_edition

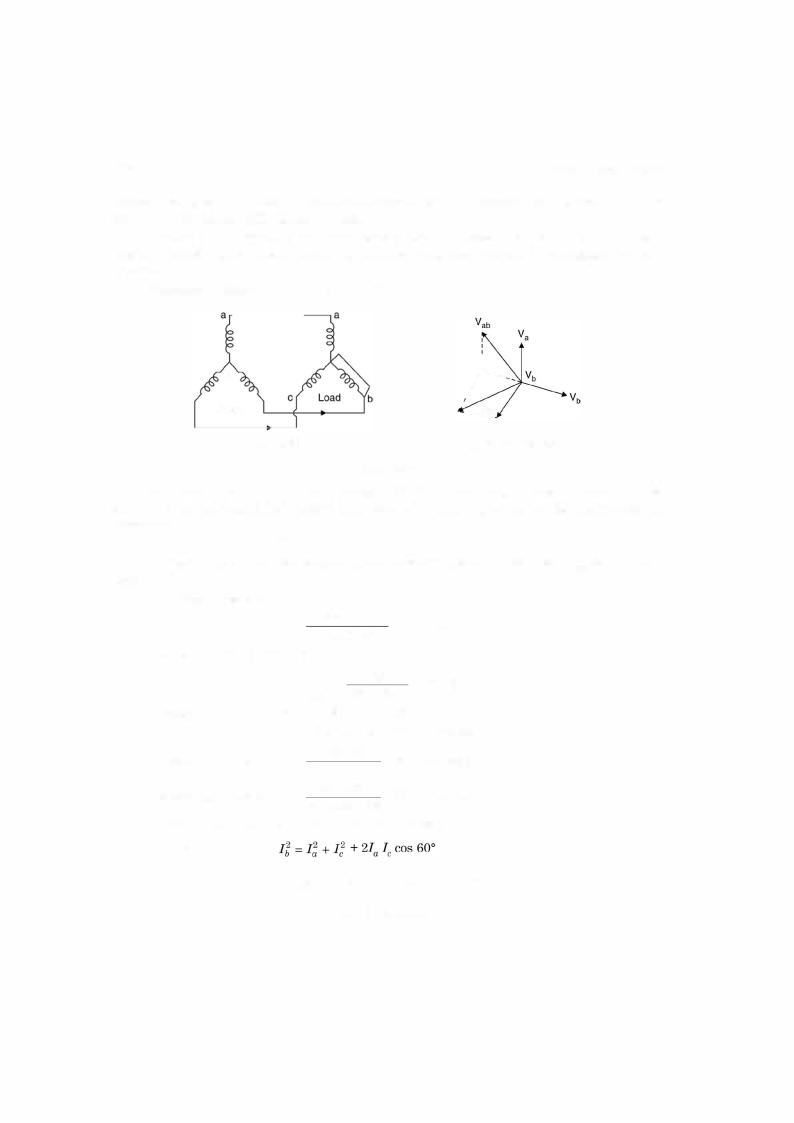
It is to be noted that whenever, in a problem, system voltage is specified, it is always to be taken as line voltage or line to line voltage, unless it is specified as phase voltage.

Let us take a few examples to illustrate what we have learnt so far.

Example 3.1. A balanced 3-phase star connected load is fed from a 208 volt 3-phase supply. Each leg of the load has a resistance of 35 Q. Determine, the power factor, the total power, the phase currents and line currents of the system.

Solution: Since it is a balanced circuit, the analysis is to be made on 1-phase basis. Also the given voltage 208 since not specified, it is to be taken as line voltage.

Hence phase voltage is 208113 = 120 volt.

Ia = 120 LO = 3.428 LOO 35

1b = 120 L - 120 = 3.428 L - 120° 35

I = 120 L 120 c 35

Since the three currents are balanced, the phasor sum of the three currents is zero. Since the load is resistive power p per phase is

FR = 3.4282 x 35 = 411.3 watts

Hence total power 3 x 411.3 ::'. 1234 watts and the load is resistive, the p.f. is unity. Since the load is star connected IL = Iph = 3.428 A.

= J3 VJL cos <j>

Using the ohmic loss formula, since resistance in each phase is 15Q, the power loss is 3 x 4.82 x 15 = 1036.8 watts. J3

In the formulae P = VLIL cos <j>, the angle <j> is the angle between the phase voltage

and the phase current corresponding to the same phase. It is to be noted with caution that the angle <j> is not the angle between the line voltage and line current or phase current but it is the