Лекция 7. Элементы теории статистических оценок и проверки гипотез.

Выборочная совокупность текста интересует лингвиста как математическая модель, с помощью которой он может оценить вероятностные характеристики всей генеральной совокупности и раскрыть закономерности нормы языка.

Переход от статистической модели выборки текста к вероятностным характеристикам норм языка связан с решением трёх задач.¹⁶

1. По характеристикам 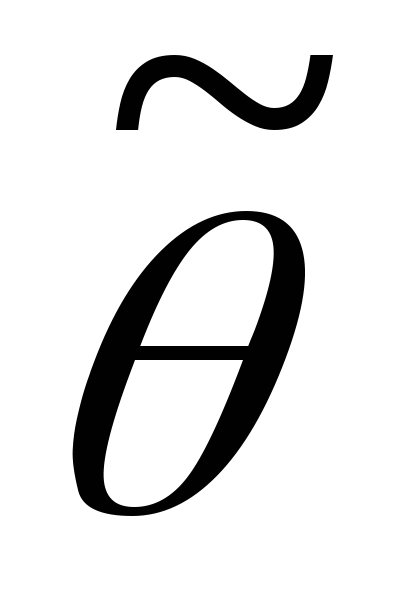вариационного ряда необходимо численно оценить скрытые от прямого наблюдения параметры соответствующего распределения генеральной совокупности, то есть параметры, выступающие в качестве вероятностных характеристик нормы языка и его разновидностей

2. По данным вариационного ряда следует оценить характер генерального распределения.

3. Имея в своём распоряжении 1 и 2 необходимо решить важнейшую технологическую задачу лингвистического исследования, состоящую в определении того, какой объём исследуемого текста даст достаточно надёжные лингвистические результаты.

7.1 Статистические оценки параметров распределения и их свойства. Оценка параметров генеральной совокупности по выборке

Статистическая оценка – приближённое значение параметра , найденное по выборке:

7.1.1. Свойства статистических оценок:

1. Несмещённость. Статистическая оценка называется несмещённой (не делается систематической ошибки в сторону завышения или занижения), если

2. Состоятельность - при увеличении числа опытов оценка приближается (сходится по вероятности) к параметру :

3.Эффективность - обладает наименьшей дисперсией:

7.1.2. Точечные оценки математического ожидания, дисперсии и вероятности.

Точечная оценка – оценка , которую используют в качестве приближённого значения параметра

Пусть - выборка, полученная в результатеn независимых наблюдений за СВ Х (чтобы подчеркнуть случайный характер, значения выборки обозначаются прописными буквами). Случайные величины можно рассматривать как n независимых случайных величин, поэтому все СВ имеют одинаковые математические ожидания и дисперсии

Тогда:

- среднее выборочное есть несмещённая и состоятельная оценка математического ожидания М(Х) генеральной совокупности.

- исправленная выборочная дисперсия есть несмещённая и состоятельная оценка дисперсии D(X) генеральной совокупности.

- частота появления события А в n независимых испытаниях есть несмещённая, состоятельная и эффективная оценка вероятности события А.

Задача 3. Для анализа лингвистических терминологических систем взято 7 фрагментов по 250 терминоупотреблений из русских лингвистических текстов. После подсчёта в каждом фрагменте числа употреблений слова «лицо» получен следующий вариационный ряд: 1,1,3,4,9,10,12.

1. Найдите по выборке несмещённую и состоятельную оценку математического ожидания М(Х) и дисперсии D(X) случайной величины Х - «число употреблений слова лицо» в русских лингвистических текстах.

2. Найдите несмещённую, состоятельную и эффективную оценку вероятности события А= «слово лицо использовано более 5 раз».