1.2. Основы теории множеств

Множество – первичное (неопределяемое) понятие всей математики. Первоначально Георг Кантор (1845-1918), создатель теории множеств описывал его следующим образом: «Множество - объединение в одно целое объектов, хорошо различимых нашей интуицией или нашей мыслью…. Множество есть многое, мыслимое нами как единое». Впоследствии, данному понятию было дано аксиоматическое определение.

1.2.1. Начальные понятия теории множеств.

1) Множества обозначаются прописными буквами, а элементы множества - строчными буквами латинского алфавита: А={a₁;a₂;…;a_n…}, где a₁;a₂;…;a_n…- элементы множества.

Например, буква Ф является элементом множества букв русского алфавита (принадлежит), а буква F- не является (не принадлежит) этому множеству.

Множество лингвистических объектов:

- множество букв в русском алфавите (или в алфавите любого другого языка);

- множество словоупотреблений (цепочка букв, заключённая между двумя пробелами) в тексте,

- множество словоформ (полностью совпадающие словоупотребления образуют одну словоформу);

- множество слов (класс семантически и грамматически связанных между собой словоформ);

- множество фонем (минимальная языковая единица, обладающая смыслоразличительной функцией);

- множество морфем (значимая часть слова естественного языка).

2) Способы задания: перечисление элементов, описание свойств.

Например: М={1,2,3} или М={x|

3).Пустое множество Ø не имеет ни одного элемента.

Пустое лингвистическое множество: множество двухбуквенных комбинаций чы, бй, оъ в русских текстах; множество дифтонгов в русском языке.

4) Равные множества состоят из одних и тех же элементов или оба пустые.

Например: а) если К={А, В, Б} и D ={ А, Б, В }, то К= D;

б) множество А={вы, вас, вам, вами} равно множеству, включающему формы склонения местоимения «вы».

5) Для наглядности множества изображаются с помощью кругов или других геометрических фигур (круги Эйлера и диаграммы Венна)

6

В

) Множество А называетсяподмножеством В,

е

А

сли все элементы множества А принадлежат множеству В

Обозначение: _.

Само множество является своим подмножеством: .

Пустое множество является подмножеством любого множества: ØВ;

Например, множество М={1,2,3} является подмножеством множества натуральных чисел N: ; множество огубленных гласных звуков [о] и [и] является подмножеством множества гласных звуков.

7) Булеан множества – множество всех его подмножеств. Обозначается: β(А).

Например: если А={f, p, q}, тогда β(А)={Ø, {f}, {p}, {q}, {f;p}, {f;q},{p;q},{f;p;q}}.

8) Числовые множества:

-

C

множество натуральных чисел, обозначаетсяN,

N

Q

Q

R

={1,2,3,…};

-множество целых чисел, обозначаетсяZ,

Z

N

={…,-2,-1,0,1,2,…};

-

множество рациональных чисел, обозначаетсяQ,

множество дробей вида

- множество действительных чисел, обозначается R, множество всех чисел, которые можно изобразить точкой числовой прямой

- множество комплексных чисел, обозначается C, множество всех чисел, которые можно изобразить точкой комплексной плоскости.

9) Эквивалентные множества – множества, между элементами которых можно установить взаимно однозначное соответствие.

10) Мощность множества – количество его элементов. Обозначается:.

Например: если В={а,в,1,2}, то =4;

Мощность множества букв русского алфавита равна 33;

мощность множества неслоговых фонем в русском языке равна1 (и), мощность множества падежей в русском языке – 6,

множество косвенных падежей имеет мощность равную 5 (все, кроме именительного).

11) Различают конечные и бесконечные множества. Бесконечные множества по мощности можно разделить на счётные и несчётные множества.

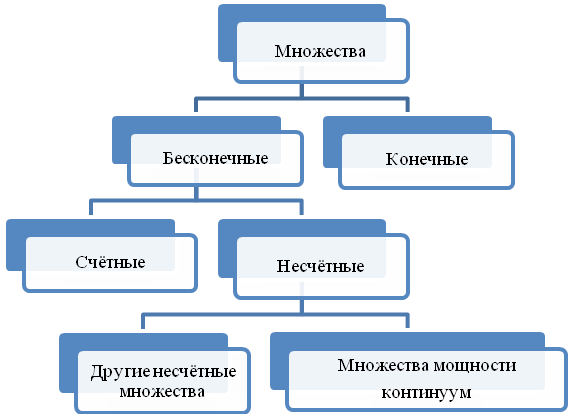Схема1

Счётное множество – это бесконечное множество, эквивалентное множеству натуральных чисел (элементы которого можно занумеровать, т.е. каждому элементу поставить в соответствие натуральное число).

Пример: множество чётных натуральных чисел, множество целых чисел, кратных 5 и т.д.

Некоторые из несчётных множеств являются множествами мощности континуум – бесконечные множества, эквивалентные множеству действительных чисел (неисчерпаемые, непрерывные).

Например: Е=[-3;5); F=[0;1] - множества мощности континуум

Лингвистика чаще имеет дело с конечными множествами, например: множество глаголов в отрывке текста; множество слов в предложении; множество букв в алфавите определённого языка; множество произведений данного автора и т.п.

Примером бесконечного лингвистического множества может быть множество всех словоупотреблений в текстах данного языка при условии, что этот язык беспрерывно порождает и будет порождать новые тексты без какого либо ограничения во времени.

1.2.2. Операции над множествами

1

В

А

. Объединение множеств А и В, обозначается,

включает элементы, принадлежащие хотя бы одному

из множеств А и В

2. Пересечение множеств А и В,

о

В

А

бозначается, включает общие элементы

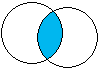
множеств А и В.

3

А

В

. Разность множеств А и В, обозначается,

включает элементы, принадлежащие множеству А,

не входящие в В.

4

А

В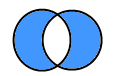

. Симметрическая разность множеств А и В,

обозначается АΔВ, включает элементы,

п

U

ринадлежащие множествам А или В, но не общие.

5

А

. Дополнение множества А доU

(U- универсальное множество), включает

элементы, принадлежащие множеству U, но не входящие в А.

Примеры. 1) А={1;2;3;4}; B={2;4;6}

={1;2;3;4;6}; ={2;4}; ={1;3}; ={6};

АΔВ={1;3;6}; ={x|

2. Операции над множествами можно проиллюстрировать с помощью множеств губных казахских согласных А = {b,p,m,w} и сонорных казахских согласных В = {m,n,n^’,w,l,r,j}:

₌{b,p,m,n,n^’,w,l,r,j}; ₌{m,w};

= {b,p}; = {n,n^’,l,r,j}; АΔВ={b,p,n,n^’,l,r,j}.

1.2.3. Отношения на множествах

Отношение – любая зависимость между элементами одного или нескольких множеств

1) Виды отношений на множествах

- унарные (1-местные), например, R={быть гласной буквой} на множестве букв алфавита естественного языка;

- бинарные (2-местные), например: R={содержать одинаковое количество букв} на множестве слов естественного языка;

- тернарные (3 –местные), например, зависимость между компонентами арифметических действий: делимое, делитель, частное;

- n – местные.

2) Свойства бинарных отношений на множестве А

Рефлексивность

Антирефлексивность

Симметричность

Антисимметричность

Транзитивность

3) Типы бинарных отношений

Эквивалентность – обладает свойствами рефлексивности, симметричности, транзитивности. Разбивает универсальное множество на непересекающиеся подмножества – классы эквивалентности.

Отношение порядка упорядочивает элементы множества, задаёт иерархию на множестве

Отношение нестрогого порядка обладает свойствами антирефлексивности, антисимметричности, транзитивности;

Отношение строгого порядка обладает свойствами рефлексивности, антисимметричности, транзитивности.

Отношения толерантности обладает свойствами рефлексивности, симметричности.

Примеры:²

1.Отношение R₁={быть родственными языками} на множестве языков мира является отношением эквивалентности, т.к. обладает свойствами рефлексивности, симметричности, транзитивности. Это отношение делит универсальное множество – множество языков мира – на группы родственных языков.

2. Отношение R₂ ={быть предком} на множестве языков мира является отношением строгого порядка, так как обладает свойствами антирефлексивности, антисимметричности и транзитивности.

3. Отношение R₃ ={содержать одинаковые слова} на множестве предложений является отношением толерантности, так как обладает свойствами рефлексивности и симметричности, но не является транзитивным.

4. Отношение порядка R= « иметь более высокий частотный ранг» на множестве слов определённого языка задействовано при создании частотных словарей. Это отношение является отношением строгого порядка, так как обладает свойствами антирефлексивности, антисимметричности и транзитивности.

5) Отношение «непосредственного заимствования» (язык Х заимствует из языка У) на множестве языков одной группы, обладает свойствами антирефлексивности, антисимметричности, и не является транзитивным.

Лекция 2. Комбинаторика. Начальные понятия теории вероятностей

Комбинаторика – раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчинённых тем или иным условиям, можно составить из заданных объектов.

«Языковеду постоянно приходится решать задачи, в которых рассматриваются комбинации и расположения элементов, принадлежащих определённому лингвистическому множеству. Так, например, синтаксисту важно знать, сколько позиционных вариантов может давать в устно-разговорной речи предложение «Сегодня идёт дождь». Фонетисту, специалисту в области кодирования текста, а также работнику ГИБДД, занимающемуся распределением букв серий автомобильных знаков на территории страны, нужно знать сколько, двух- и трёхбуквенных комбинаций может дать русский алфавит»³.

2.1.1. Правила комбинаторики

Пусть элемент можно выбратьспособами;–способами;…,–способами.

Тогда:

1) элемент

можно выбрать способами;

2) элемент

можно выбрать способами .

2,2. n! (n-факториал) – произведение n первых натуральных чисел.

1! =1; 2!=12=2; 3!= 123=6; 4!= 1234=24; …..

n!= 123…n (при n>3) 0!=1