6.2. Статистическое распределение выборки и его графическое изображение

Пусть изучается СВ Х (генеральная совокупность) относительно некоторого признака. Проводится ряд независимых испытаний. В результате опытов СВ Х принимает некоторые значения. Совокупность полученных значений представляет собой выборку, а сами значения являются статистическими данными.

Первоначально проводят ранжирование выборки - расположение статистических данных выборки по неубыванию. Получаем вариационный ряд.

Вариационный ряд - проранжированная выборка.

6.2.1. Дискретный статистический ряд

Если генеральная совокупность является дискретной СВ, строится дискретный статистический ряд (статистическое распределение).

Пусть значение появилось в выборке раз,

- разa , …, - раз.

- i-тая варианта выборки; - частота i-той варианты Частота показывает, сколько раз данная варианта появилась в выборке.

- относительная частота i-той варианты

(показывает какую часть выборки составляет ).

Статистическое распределение – это соответствие между вариантами выборки и их частотами или относительными частотами.

Для ДСВ статистическое распределение можно представить в виде таблицы – статистического ряда частот или статистического ряда относительных частот.

Статистический ряд частот Статистический ряд

относительных частот

			........
			........

			........
			........

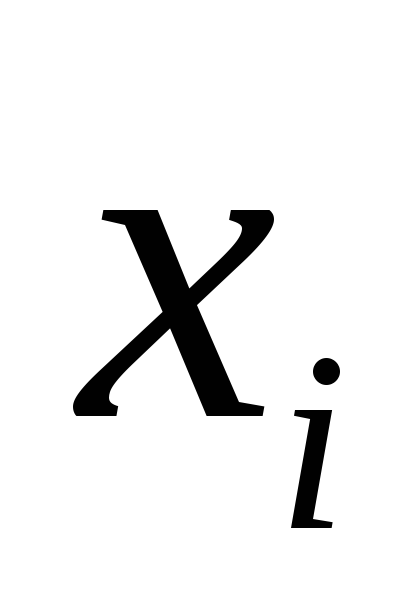
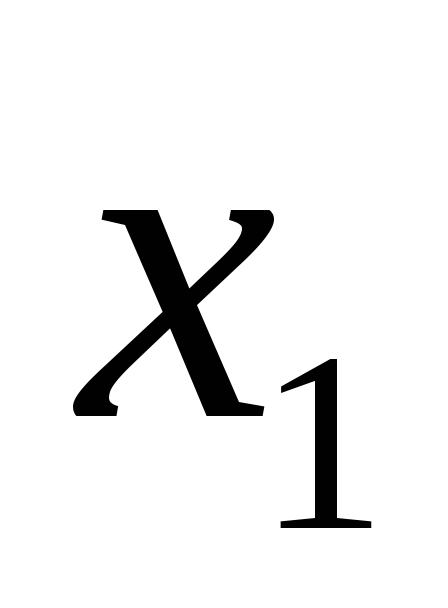
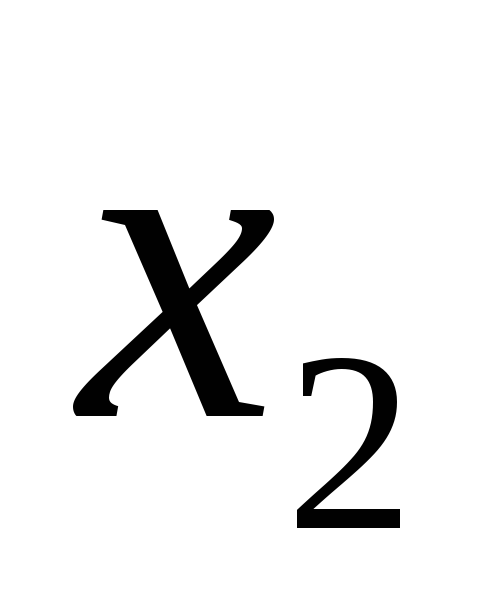
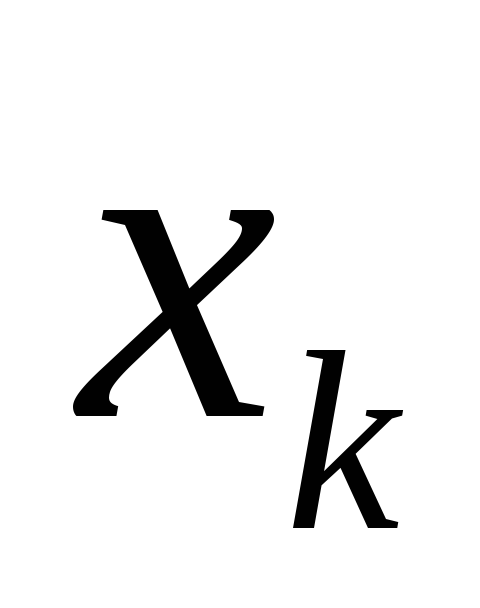
Полигон частот (относительных частот) – графическое изображение дискретного статистического ряда - ломаная линия, последовательно соединяющая точки [ для полигона относительных частот].

x_i

Задача1. Исследуется длина словоупотреблений в прозе Зинаиды Гиппиус. Произвольно выбран отрывок текста длиной 10 слов и подсчитано количество букв. Получены следующие данные: 1,3,2,5,1,8,6,7,7,1. Представить выборку в виде вариационного ряда, построить статистический ряд частот и относительных частот, изобразить полигон относительных частот для полученного ряда.

6.2.2. Интервальный статистический ряд

Если генеральная совокупность является непрерывной СВ. (значения выборки практически не повторяются, частота почти каждой варианты равна единице), то строится интервальный статистический ряд вида:

			…
			…
			…

где - частота попадания значений выборки в i-тый интервал;

- относительная частота попадания в i-тый интервал.

Оптимальная ширина интервалаh определяется по формуле Стерджеса: , начало первого интервала:

Г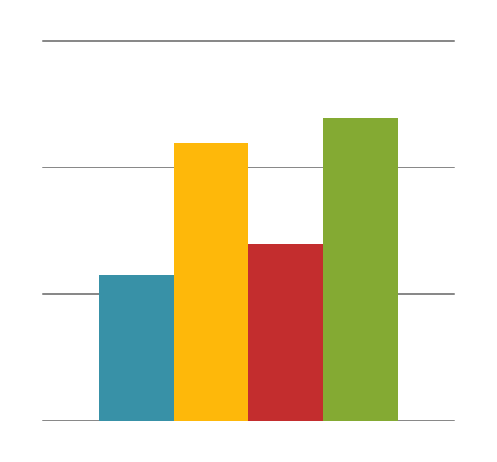рафическое изображение интервального статистического ряда – гистограмма частот или относительных частот – совокупность прямоугольников с основанием равнымh и высотой / h для гистограммы частот или / h для гистограммы относительных частот.

Задача 2:

В ходе исследования длины китайского слога произведено 50 замеров времени звучания слогов, произнесённых дикторами-китайцами, причём длины слогов колеблются от 40 до 300мс, практически не повторяясь:

73	117	40	211	191	129	136	150	167	142
178	138	156	210	93	137	149	180	212	141
125	106	138	115	123	102	89	153	180	75
131	125	148	110	198	222	128	107	127	100
57	243	163	160	300	218	179	264	115	183

Таблица 1

Построить интервальный статистический ряд по приведённым данным. Изобразить гистограмму относительных частот полученного распределения.