4.5. Законы распределения случайных величин.

Биномиальное распределение и распределение Пуассона - законы распределения ДСВ, которые могли бы выступать в качестве наиболее адекватных математических моделей порождения текста и составляющих его языковых единиц

1) Биномиальный закон распределения.

Дискретная случайная величина Х распределена по биномиальному закону, если она может принимать значения 0, 1, 2, …, n

с вероятностями, которые находятся по формуле Бернулли:

где

Пример. Составить закон распределения числа попаданий в цель при двух выстрелах, если вероятность попадания при одном выстреле равна 0,4. Найти М(x) и D(x).

Биномиальное распределение СВ используется при описании употребления фонем, графем и их классов, а так же при описании грамматических категорий, при условии, что n – количество испытаний и m - число появлений события А, невелико. В конкретных лингвистических задачах это условие не всегда соблюдается.

Будем рассматривать последовательные появления интересующей нас языковой единицы А в тексте в качестве потока лингвистических событий. Примерами такого потока могут служить последовательные появления в русском связном тексте словоформы «моря», или словосочетания «у самого синего моря» и т.п. Вероятность появления словоформы моря в большом тексте мала. Для описания редких лингвистических событий используется распределение Пуассона.

2) Закон Пуассона

Дискретная случайная величина Х распределена по закону Пуассона закону, если она может принимать значения 0, 1, 2, …, n

с вероятностями, которые находятся по формуле Пуассона:

Пример. Вероятность появления опечатки на определённой странице текта, содержащего 200 страниц, равна 0,01. Определить:

а) вероятность появления трёх опечаток в тексте;

б) вероятность того, что количество опечаток будет больше трёх;

в) М(Х) и D(X) СВ Х= «количество опечаток в тексте».

3) Нормальное распределение (закон Гаусса)

Распределение непрерывных СВ описывается специальными законами, среди которых , наиболее важным является нормальное распределение (закон Гаусса). Нормальное распределение выступает в качестве предельного закона, к которому при определённых условиях приближаются другие теоретические распределения.

НСВ Х распределена по нормальному закону Х~N(a;σ), если её функция плотности распределения имеет вид:

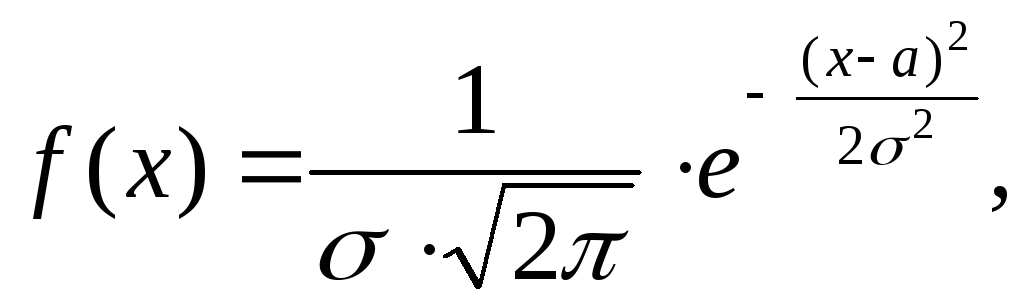
где а и σ>0 – параметры нормального распределения.

Свойства функции плотности вероятности f(x)

нормального распределения.

1) f(x)>0,

2) Прямая х=а – ось симметрии графика f(x);

3) - единственная точка экстремума функции f(x);

4) - точки перегиба графика f(x).

График f(x) - кривая нормального распределения (кривая Гаусса)

- имеет идеально симметричную форму,

коэффициенты асимметрии и эксцесса

для нормального распределения равны нулю.

При а=0 и σ=1, нормальное распределение называется стандартным. Плотность вероятностистандартной СВ имеет вид:

Функция распределения СВ Х~N(0;1) определяется по формуле:

и называется функцией Лапласа.

Стандартное нормальное распределение часто используется в статистических исследованиях, поэтому значения функции Лапласа табулированы.

Пример: Случайная величина Х задана дифференциальной функцией распределения :

По какому закону распределена случайная величина?

Найти М(х), D(х), σ(x).

Построить схематически график f(x)