3.4. Теорема Пуассона

Из замечания 3.2 следует, что точность вычисления вероятностей тем хуже, чем меньше р или q. Возникает задача отыскания асимптотической формулы, специально приспособленной для этого случая. Такая формула была получена Пуассоном.

Теорема 3.3. Если число испытаний велико, а вероятность появления события А в каждом испытании мала, то имеет место приближенная формула

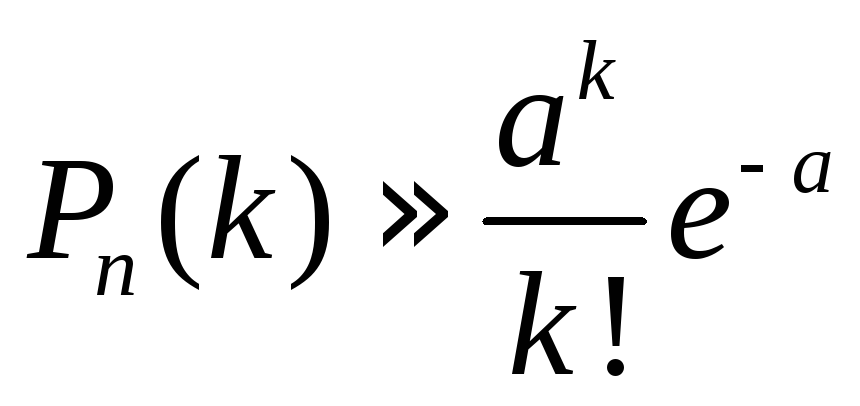или , (3.5)

где  среднее число появлений события А в п испытаниях.

Замечание 3.3. Не сложно проверить, что при больших п справедливо равенство

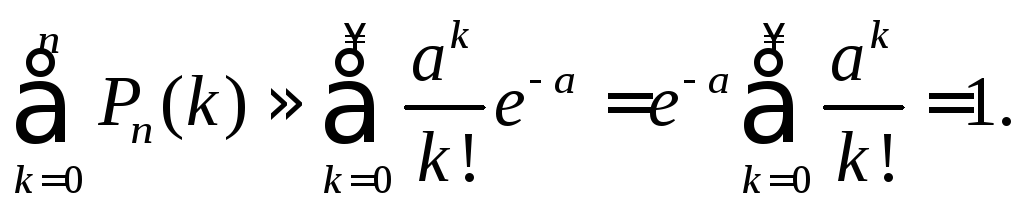
Пример 3.9. Вероятность того, что деталь окажется бракованной, равна 0,01. Найти вероятность того, что среди 400 изготовленных деталей ока-жется ровно пять бракованных.

Так как число испытаний велико, а вероятностьмала, то воспользуемся формулой (3.5). Найдёми тогда

Замечание 3.4. Для удобного использования формулы Пуассона также существует таблица для (прил.3). Имеется таблица (прил. 4) и для вычисления вероятностей вида

(3.6)

причем поскольку в формуле Пуассона число испытаний достаточно велико, то п можно не писать, т.е. и

Пример 3.10. Вероятность того, что деталь будет забракована, равна 0,01. Найти вероятность того, что среди 400 изготовленных деталей будет не больше пяти забракованных.

Очевидно, что поэтому можем воспользо-ваться формулой (3.6). Из таблицы (прил.4), учитывая, что и, находимСледовательно, искомая вероятность равна

3.5. Вероятность отклонения частоты от постоянной вероятности в независимых испытаниях

Пусть производится п независимых испытаний с постоянной веро-ятностью р. Требуется найти вероятность того, что отклонение частоты отр по абсолютной величине не превосходит данного , т.е.

Преобразуем неравенство в скобках

и умножим полученное неравенство на

Полагая в формуле (3.3) 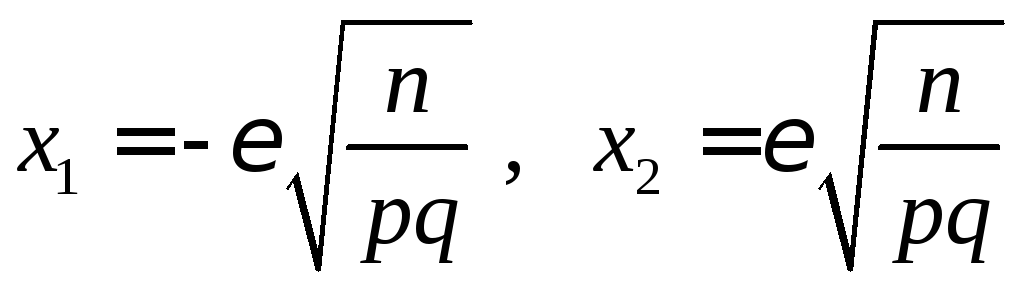и учитывая нечетность функции Лапласа, получаем

. (3.7)

Пример 3.11. Вероятность изготовления фарфоровой посуды высшего качества равна . Найти вероятность того, что в партии из 600 изде-лий частота изготовления посуды высшего качества отклонится от веро-ятности не более чем на.

Подставим данные задачи в формулу (3.7)

Определим то количество k фарфоровой посуды высшего качества, которое удовлетворяет полученному условию. Для этого раскроем модуль

неравенства 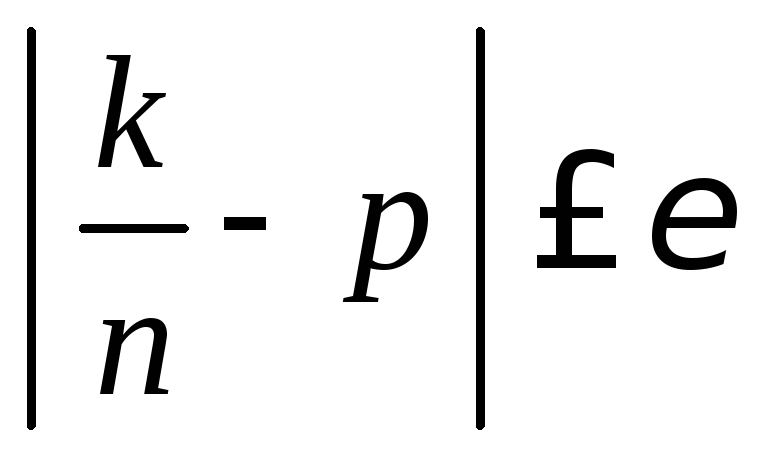, в результате чего получим двойное неравенство

(3.8)

Подставляя в полученное неравенство (3.8) значения данных задачи, найдем, что с вероятностью 0,9876 количество k фарфоровой посуды высшего качества в партии удовлетворяет условию

или

Пример 3.12. Вероятность появления события А (например, изготов-ление бракованного изделия) в каждом из независимых испытаний равна 0,04. Найти число испытаний п (количество выпускаемых изделий), при котором с вероятностью 0,9544 можно ожидать, что отклонение частоты появления события А (числа бракованных изделий) от заданной вероят-ности не превысит 2%.

По формуле (5), учитывая, что получим

По таблице значений функции Лапласа находим соответствующее значение аргумента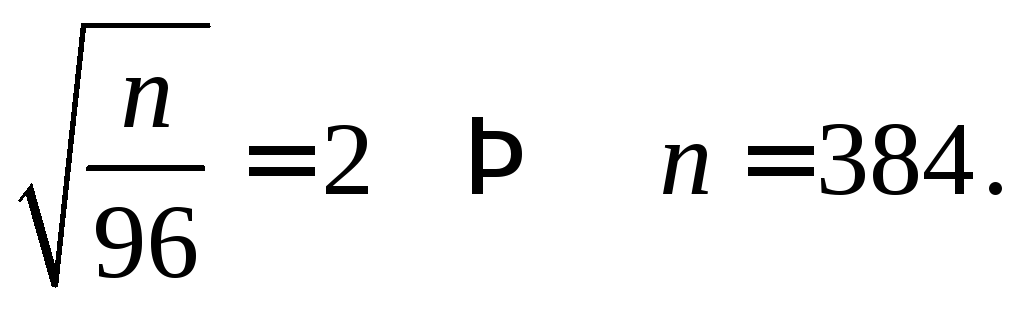

Таким образом, количество появления события А (число бракованных изделий) будет удовлетворять условию

или