X и y независимые случайные величины.
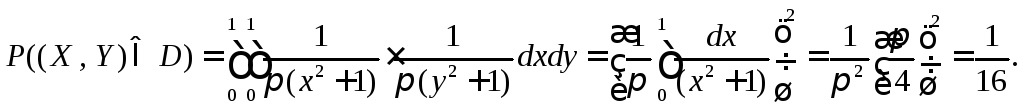
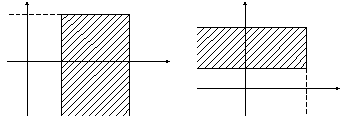
8.2. Вероятность попадания двумерной случайной величины
в полуполосу и прямоугольник
Из определения
функции распределения несложно найти
вероятность попадания двумерной
случайной величины в полуполосу
и
(рис.а)
или в полуполосу
и
(рис.б).
Y
Y
у
X
X
x
a б
Вычитая из
вероятности попадания двумерной
случайной величины
в квадрант с вершиной
вероятность попадания случайной
величины
в квадрант с вершиной
получим (рис.
а)
Аналогично для полуполосы (рис. б)
П
оскольку
прямоугольник можно представить как
разность полуполос, то вероятность
попадания двумерной СВ
в прямоугольник можно найти вычитанием
из вероятностиY
попадания
д
вумерной
СВ
в полуполосу
и
вероятности
попадания
д
вумерной
СВ
в полу-
полосу
и
.
X
Таким образом, имеем
Замечание 1.
Если функция плотности
непрерывна, то полу-ченная формула
соответствует свойству2.
8.3. Числовые характеристики двумерной случайной величины
Числовые характеристики составляющих двумерной случайной вели-чины вводятся также как и для одномерной. Кроме рассмотренных числовых параметров вводятся и такие, которые характеризуют зависимость состав-ляющих X и Y.
Определение 8.4. Ковариацией двумерной случайной величины назы-вается
.
После простых преобразований можно получить
.
Очевидно,
.
По определению дисперсии для суммы
слу-чайных величинX
и Y
имеем
.
Тогда для независимых
случайных величин
.
Таким образом, если
,
то случайные величиныX
и Y
зависимы.
Для характеристики степени зависимости случайных величин X и Y используется безразмерный коэффициент корреляции
.
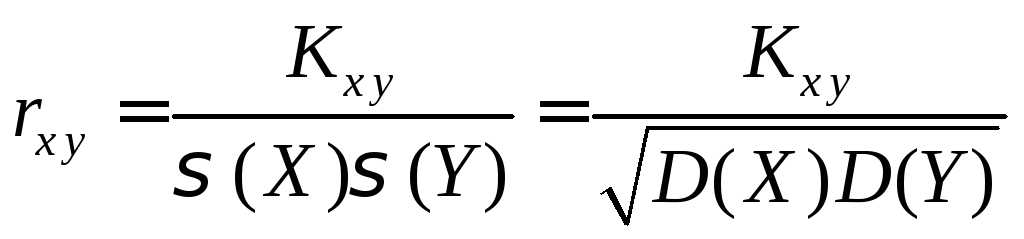Отметим его основные свойства.
1.
Если случайные величины X
и Y
независимы, то
.
Обратное, вообще говоря, неверно.
2.
Если
,
гдеА
и В
const,
то
.
Действительно,
обозначим
,
тогда
и
После этого
получаем
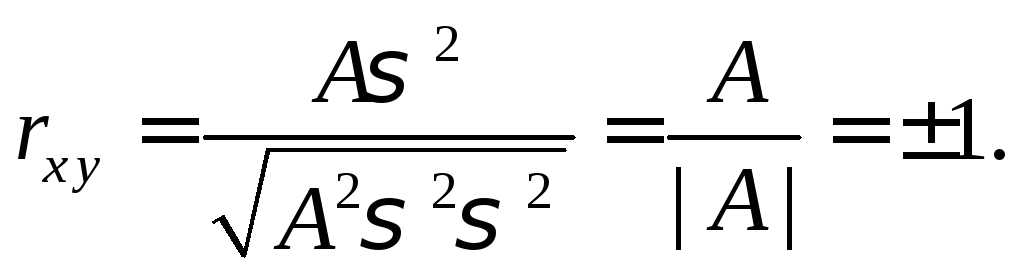
3.
.
Замечание 2. Из определения и свойств коэффициента корреляции следует, что он оценивает линейную связь между случайными величинами X и Y. При этом:
1.
функциональная линейная связь.
2.
статистическая зависимость.
3.
линейная связь отсутствует.
Пример 8.2. Закон распределения двумерной случайной величины (X, Y) задан таблицей
|
Y X |
3 |
10 |
12 |
|
4 |
0,17 |
0,13 |
0,25 |
|
5 |
0,1 |
0,3 |
0,05 |
Найти законы распределения составляющих компонент и их числовые характеристики.
Проводя суммирование по соответствующим строкам и столбцам, получаем
-
Y
4
5
Х
3
10
12
p
0,55
0,45
p
0,27
0,43
0,3
Вычислим числовые характеристики:
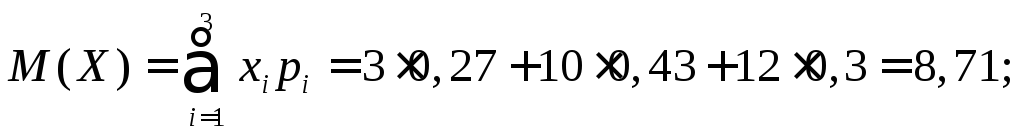
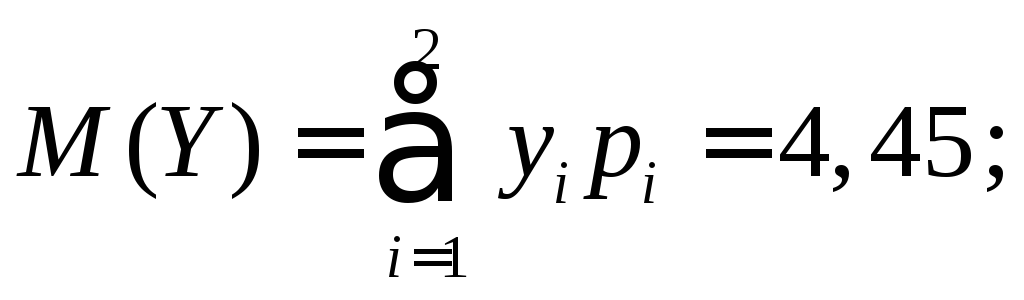
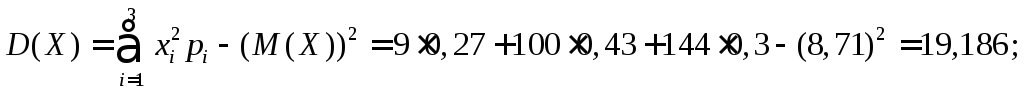
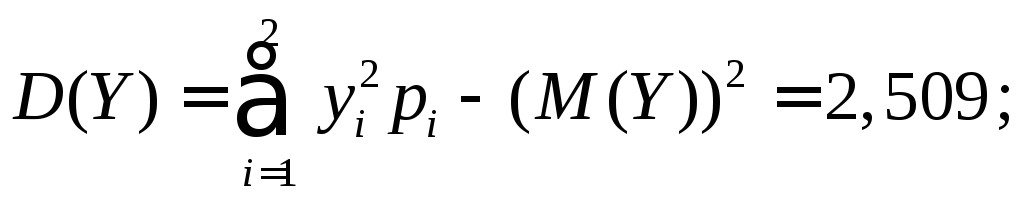
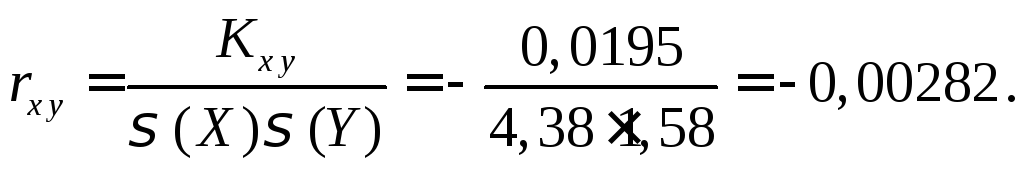
Найденный коэффициент корреляции мал, следовательно, случайные величины X и Y слабо зависимы.