1. Статистические законы распределения выборки

1.1. Вариационный ряд

Пусть из генеральной совокупности извлечена выборка, причем значение наблюдалось , ,…, раз и объём выборки.

Наблюдаемые значения называютсявариантами. Количество наблюдений значенияназываетсячастотой, а величина отно-

сительной частотой.

Определение 1.1. Статистическим распределением выборки называется перечень вариант и соответствующих им частот.

			…
			…

Если варианты выборки расположены в возрастающем порядке, то такое статистическое распределение называется вариационным рядом.

Для лучшего восприятия статистического распределения выборки при-нято осуществлять графическую интерпретацию полученного вариацион-ного ряда.

1.2. Полигон и гистограмма

1. Рассмотрим случай дискретной СВ.

Определение 1.2. Полигоном частот называется ломаная, отрезки ко-торой соединяют точки

Аналогично определяется полигон относительных частот  ломаная, отрезки которой соединяют точки

Пример 1.1. Построить полигон относительных частот по данному распределению выборки

	2	4	5	6	8
	10	40	20	15	15

Здесь 10 + 40 + 20 + 15 + 15 = 100.

Вычислим относительные частоты:

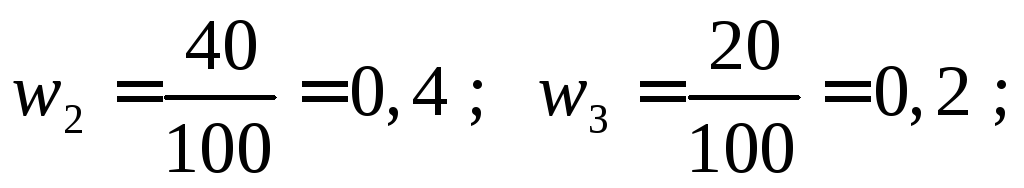
w

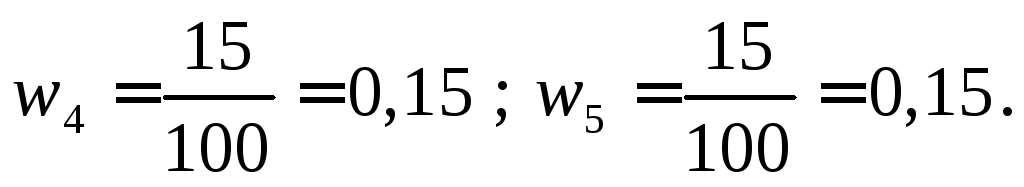0,4

0,2

0,1

0 2 4 5 6 8 x

2. Случай непрерывного распределения выборки.

В этом случае весь интервал, в котором заключены все наблюдаемые значения исследуемого признака, разбивают на ряд частичных интервалов длины h и находят  сумму частот вариант, попавших в i-й интервал.

Рекомендуется выбирать длину интервала по формуле

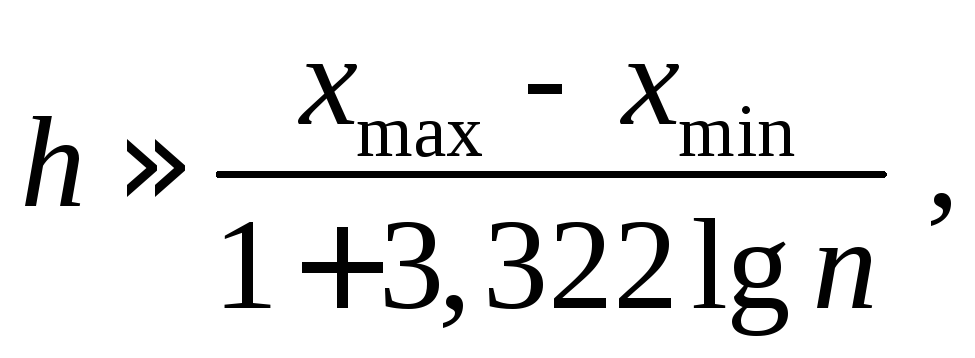
которая для часто встречающихся случаев п = 50 и п = 100 будет иметь вид исоответственно. Тогда получим не более 10 интервалов

что удобно для дальнейших вычислений.

Таким образом, мы получаем интервальный вариационный ряд сле-дующего вида

			…
			…

Определение 1.3. Гистограммой частот называется ступенчатая фигура, состоящая из прямоугольников с основанием h и высотой  плотность частоты.

Аналогично определяется гистограмма относительных частот .

Из определения следует, что гистограмма относительных частот приближенно определяет плотность распределения вероятности случай-ной величины.

Пример 1.2. По данным выборки построить гистограмму частот

i
1		10	2,5
2		20	5
3		50	12,5
4		12	3
5		8	2

Здесь 10 + 20 + 50 + 12 + 8 = 100, а

12,5

5,0

2,5

0 1 5 9 13 17 21 x

1.3. Эмпирическая функция распределения

Пусть известно статистическое распределение выборки. Введём обозна-чения:  число вариант меньших x; n  объём выборки.

Определение 1.4. Эмпирическая функция распределения определяется формулой .

В отличие от эмпирической функции распределения функциюназывают теоретической функцией распределения. При достаточно больших значенияхn эмпирическая функция близка к теоретической, что следует из теоремы

Теорема. Для любого значения варианты х и для любого имеет место

Таким образом, эмпирическая функция распределения выборки служит для оценки (приближенного выражения) теоретической функции распреде-ления генеральной совокупности.

Пример 1.3. Построить эмпирическую функцию распределения по данному распределению выборки.

	2	3	5
	5	20	25

Здесь п = 5 + 20 + 25 = 50, а относительные частоты

Тогда получим:

1. Если , то

2. Если , то

3. Если , то

4. Если , то

1

0,5

0,1

0 2 3 5 х