4.3. Корреляционная таблица

При большом числе наблюдений одно и то же значение случайной величины Х может встретиться раз, одно и то же значение случайной величиныY может встретиться раз, а одна и та же пара чисел (х, у) может наблюдаться раз. Поэтому данные наблюдений группируют, т.е. подсчитывают частоты,,. Все сгруппированные данные за-писывают в виде таблицы, которую называют корреляционной.

Поясним ее строение на простом примере. Имеем таблицу:

Y X	1	2	3	4	5
1				6	4	10
0			1	4	6	11
1		5	9	5		19
2	3	7				10
	3	12	10	15	10

В первой строке указаны наблюдаемые значения (1, 2, 3, 4, 5) слу-чайной величины Х, а в первом столбце таблицы – наблюдаемые значения (1, 0, 1, 2) случайной величины Y. На пересечении строк и столбцов находятся частоты наблюдаемых пар значений случайных величин Х и Y. Например, частота 6 указывает, что пара чисел (4, 1) наблюдалась 6 раз. Все частоты помещены в прямоугольнике, стороны которого проведены жирными линиями.

В последнем столбце записаны суммы частот строк. Например, сумма частот второй строки равна - это число указывает, что значение случайной величины Y, равное 0 (в сочетании с различными значениями случайной величины Х ), наблюдалось 11 раз.

В последней строке записаны суммы частот столбцов. Например, сумма частот четвертого столбца равна - это число указывает, что значение случайной величины Х, равное 4 (в сочетании с различными значениями случайной величины Y ), наблюдалось 15 раз.

Общее число наблюдений

4.4. Выборочный коэффициент корреляции

Ранее мы полагали, что значения Х и соответствующие им значения Y наблюдались по одному разу. На практике, безусловно, одна пара случайных величин (х, у) может наблюдаться любое число раз.

Поэтому формула для коэффициента регрессии (4.4) примет вид

(4.5)

где в сумме учтено, что пара (х, у) наблюдалась раз, а и выборочные средние квадратические отклонения случайных величин Х и Y.

Умножим обе части равенства (4.5) на дробь и назовем это выражение выборочным коэффициентом корреляции

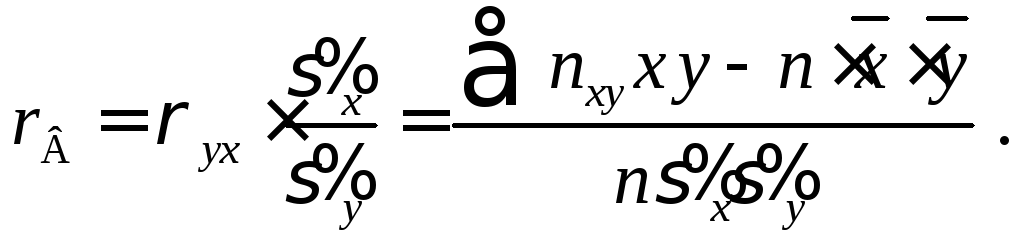
Тогда уравнение линейной регрессии Y на Х будет иметь вид

Замечание 2. Выборочный коэффициент корреляции является безраз-мерной оценкой коэффициента регрессии

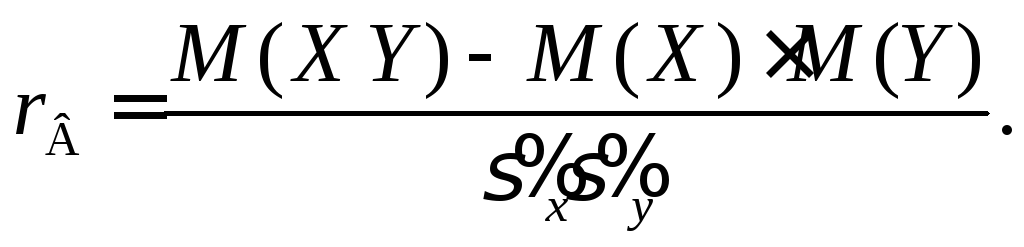
Таким образом, основная задача корреляционного анализа состоит в оценке степени линейной связи между случайными величинами Х и Y, которая устанавливается при помощи выборочного коэффициента корре-ляции

Если выборочный коэффициент корреляции мал, то линейная связь считается слабой и ее можно не принимать во внимание. Если же выборочный коэффициент корреляцииблизок к1, то линейная связь сильная и к ней следует относиться практически как к функциональной. В противном случае, связь принято считать статистической. И, наконец, при связь между случайными величинамиХ и Y имеет строго линейный характер.

Замечание. Выборочный коэффициент корреляции является лишь оценкой теоретического коэффициента корреляциигенеральной сово-купности, поэтому возникает необходимость проверить гипотезу о значи-мости выборочного коэффициента корреляции. Однако, если выборка имеет достаточно большой объем и хорошо представляет генеральную совокупность, т.е. является репрезентативной, то вывод (гипотезу) о ли-нейной зависимости между случайными величинами Х и Y , полученный по данным выборки, можно распространить и на всю генеральную сово-купность.

Например, для оценки теоретического коэффициента корреляции генеральной совокупности (если она распределена нормально) можно воспользоваться формулой