Министерство образования и науки Украины

Донецкий национальный технический университет

Улитин Г.М., Гончаров А.Н.

Курс лекций

по высшей математике

Часть III

Учебное пособие

Донецк  2010

УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ

Лекция № 50.

1. Основные типы уравнений математической физики

Для дифференциальных уравнений второго порядка в частных произ-водных существуют три типа уравнений или уравнений, сводящихся к ним путём замены переменных:

1. Уравнения гиперболического типа.

К этому уравнению приводятся задачи о различных колебательных процессах. Простейший (канонический) вид этого уравнения

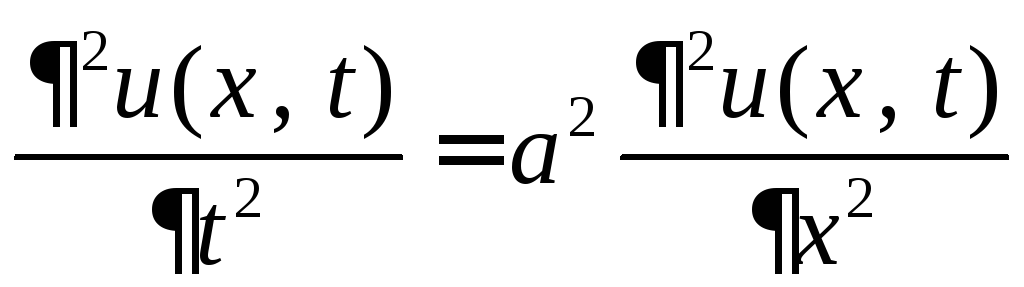волновое уравнение.

2. Уравнения эллиптического типа.

К этому уравнению приводятся задачи об электрических и магнитных полях, задачи гидродинамики жидкости, диффузии, упругости. Каноничес-кий вид этого уравнения

уравнение Лапласа.

3. Уравнения параболического типа.

К этому уравнению приводятся задачи о распространении тепла, фильтрации жидкости и газа. Канонический вид этого уравнения

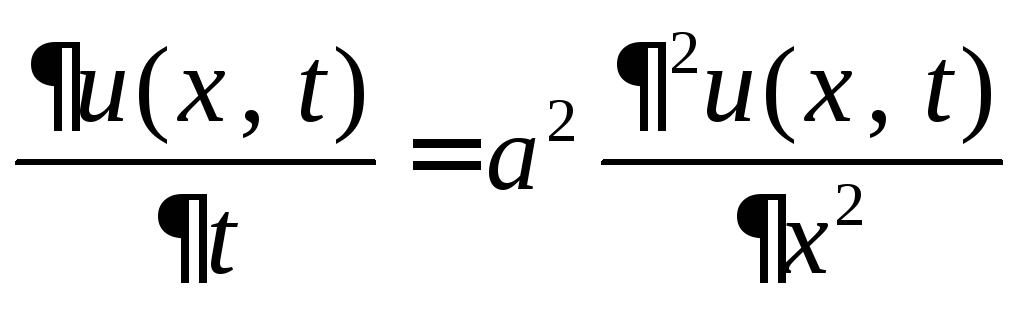уравнение Фурье или теплопроводности стержня.

Остановимся более подробно на случае волнового уравнения.

2. Решение волнового уравнения методом Фурье

Рассмотрим задачу о колебаниях струны, закреплённой в точках и. Уравнение её поперечных колебаний имеет вид

, (1)

где  поперечное смещение струны, 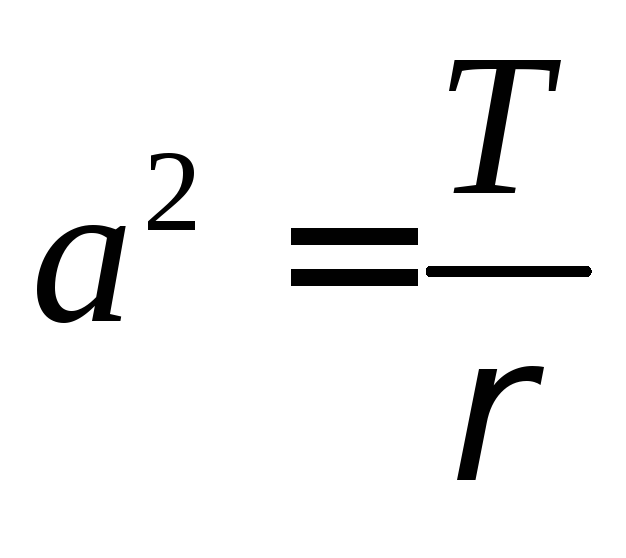,T  сила натяжения струны, - линейная плотность струны.

Для решения уравнения (1) необходимо задать граничные условия (условия неподвижности концов струны):

(2)

и начальные условия (форма струны и скорость каждой точки струны в момент времени ):

(3)

. (4)

Замечание 1. Если и, то струна находится в покое и.

Решение уравнения (1) будем искать в виде произведения двух функций

. (5)

Подставим выражение (5) в уравнение (1), получим

или . (6)

В левой части равенства (6) стоит функция от t, а в правой  от x. Поэтому такое равенство возможно только при условии

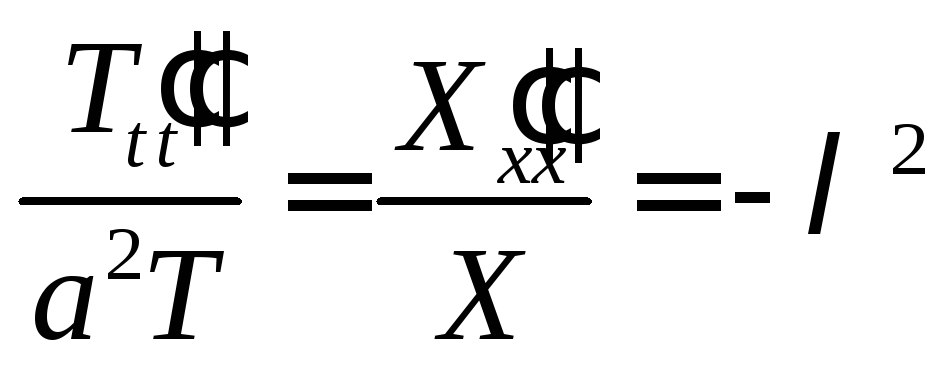или

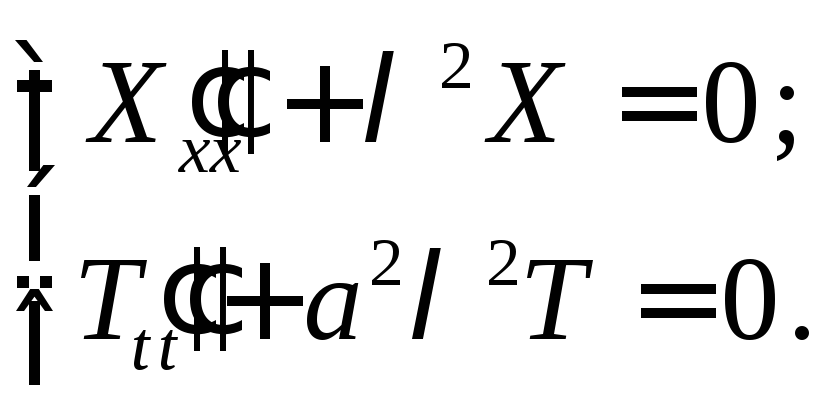
Общие решения этих дифференциальных уравнений имеют вид

,

тогда

(7)

Подберём произвольные постоянные , чтобы они удовлетворяли начальным и граничным условиям. Подставив выражение (7) в граничные условия (2), получим систему

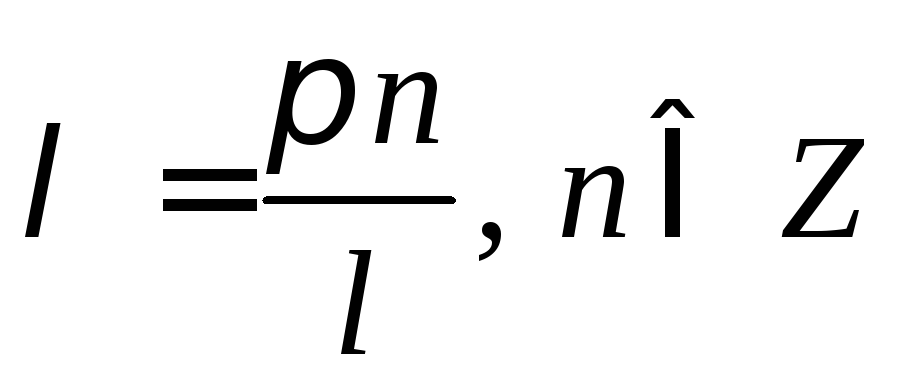Последнее равенство возможно только при , т.е.и.

Найденные значения 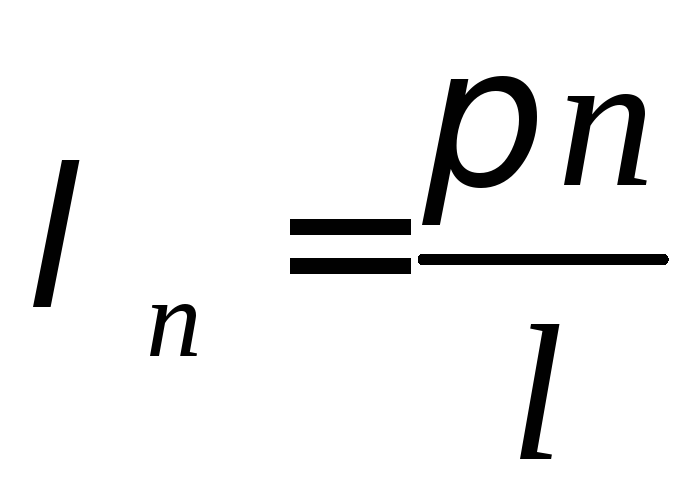называютсясобственными значениями, а функции  собственными функциями.

Замечание 2. Константу разделения нельзя взять положительной величиной, т.е. в виде , так как для этого случая решение

не удовлетворяет граничным условиям ни при каких значениях .

Таким образом, для каждого значения п получаем своё решение

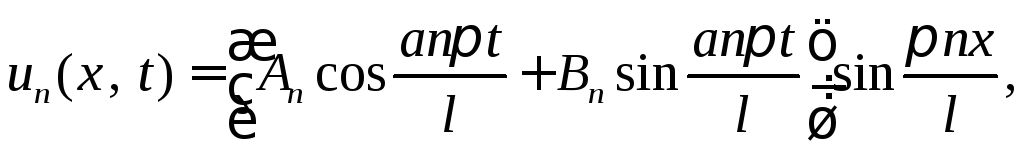
а сумма этих решений также является решением уравнения (1), т.е.

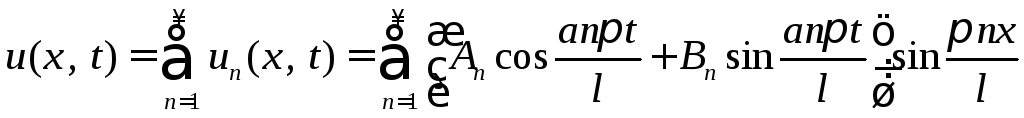. (8)

Теперь удовлетворим начальные условия. Подставим в условие (3) выражение (8), положив ,

.

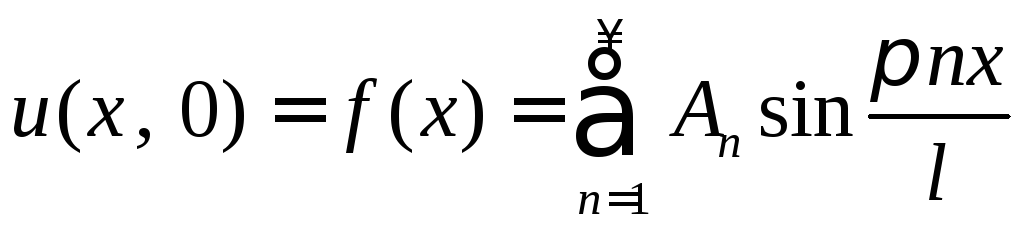Замечаем, что коэффициенты являются коэффициентами Фурье разложения функциив ряд по синусам и тогда

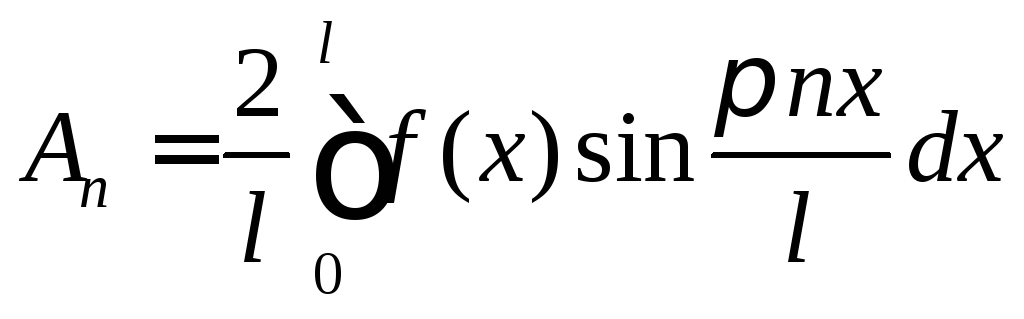. (9)

Продифференцируем выражение (8) по t и подставим , получим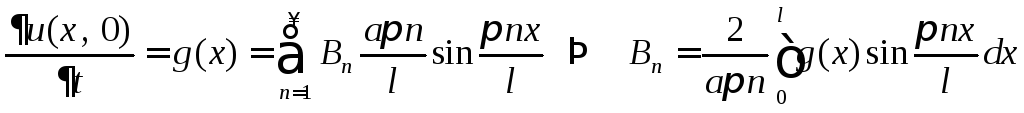. (10)

Окончательно, решение уравнения (1), удовлетворяющее условиям (24), имеет вид (8), где коэффициенты ивычисляются по формулам (9-10).

Пример. Решить волновое уравнение 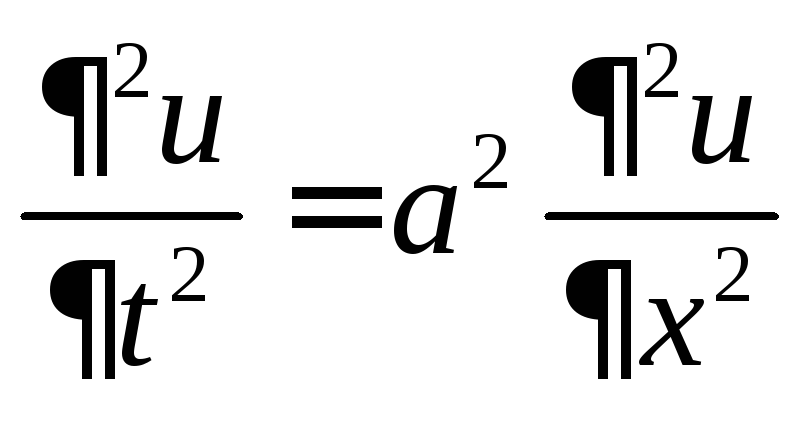при граничных условиях:и начальных условиях:

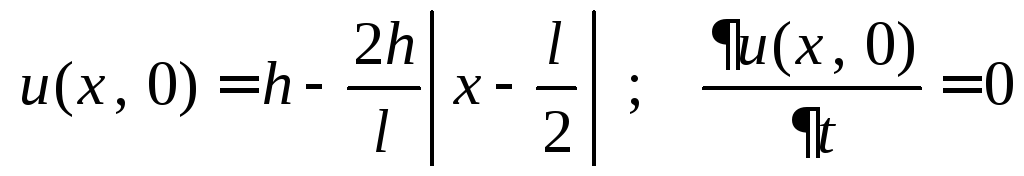. и

Так как , тоM

, h K

где уравнения прямых ОМ и МК: О l x

и тогда находим

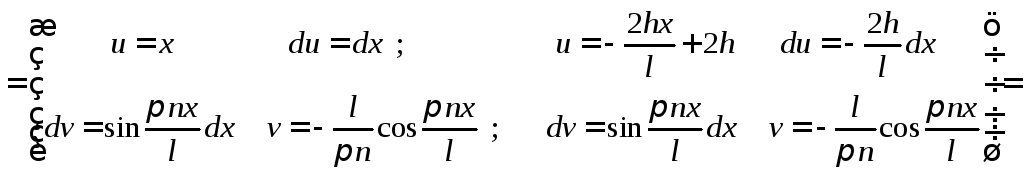
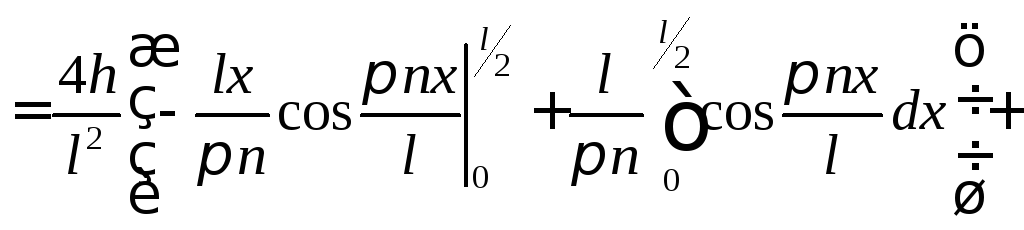
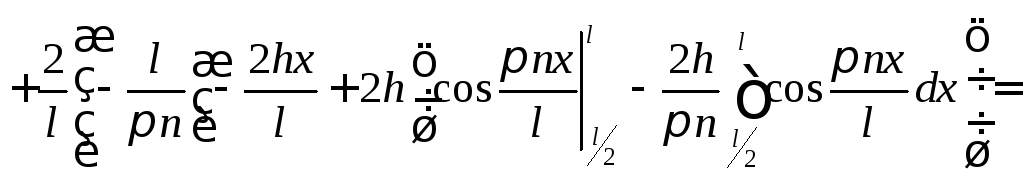
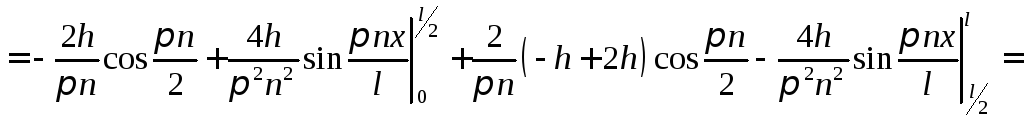
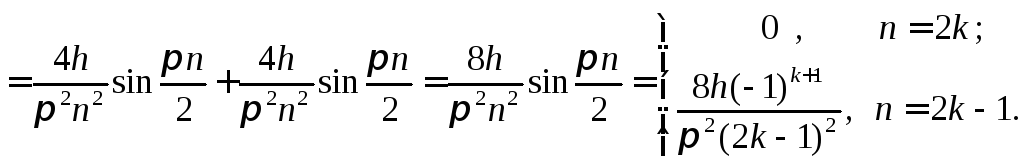
Тогда

.

Если обозначить 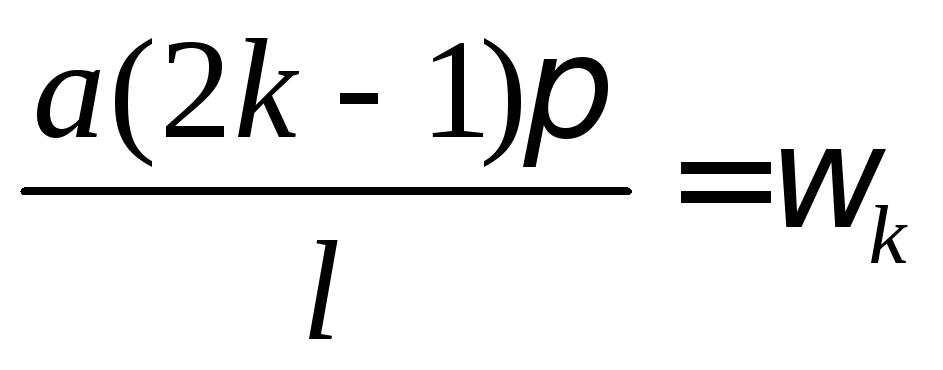, то

.

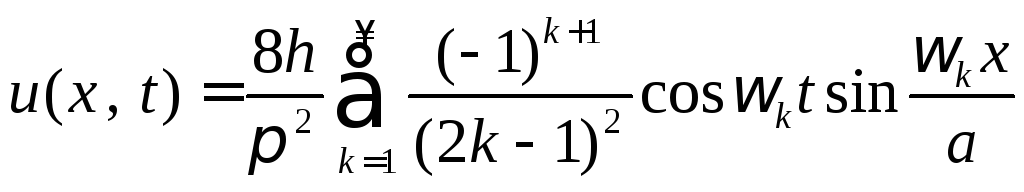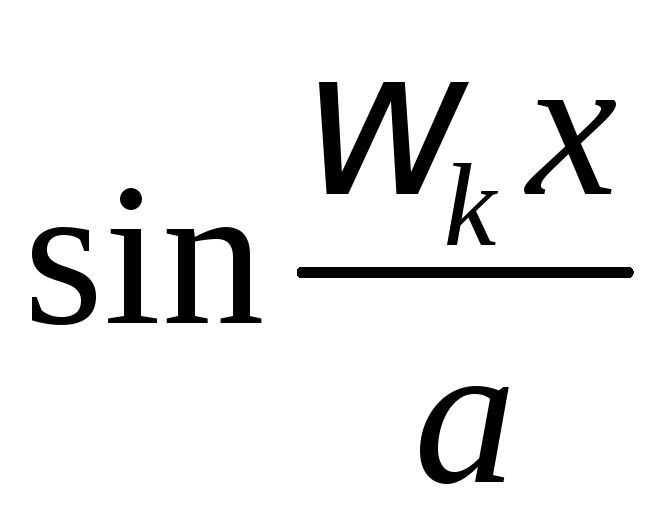
Здесь  частоты колебаний,  формы колебаний с соот-ветствующими амплитудами .
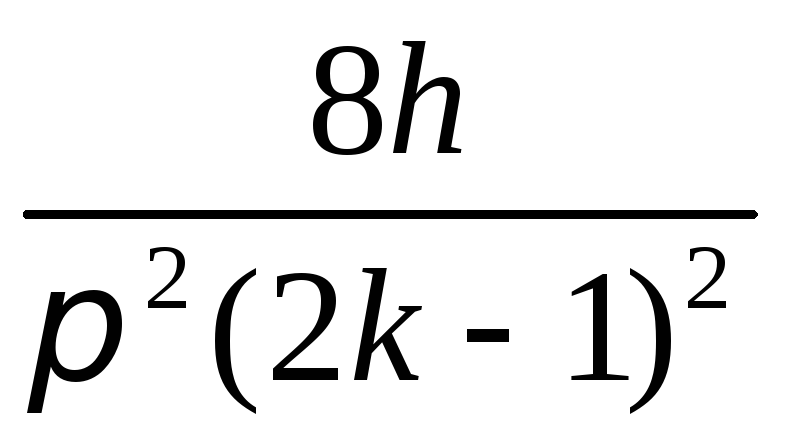