1.2. Эмпирическая функция распределения

Пусть известно статистическое распределение выборки. Введём обозна-чения:  число вариант меньших x; n  объём выборки.

Определение 5. Эмпирическая функция распределения определяется формулой .

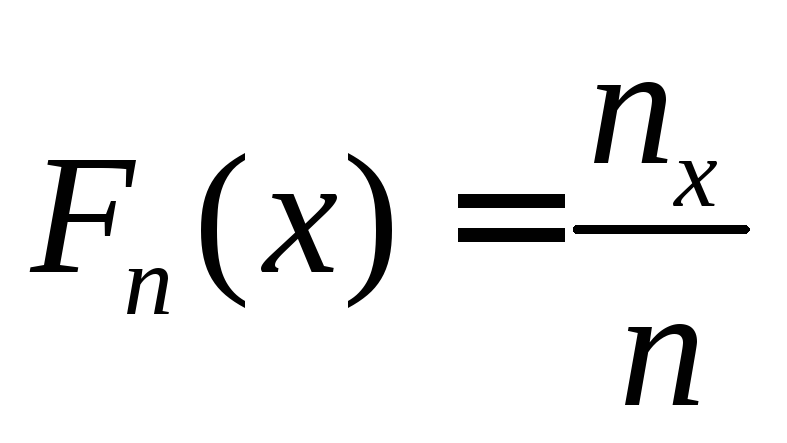В отличие от эмпирической функции распределения функциюназывают теоретической функцией распределения. При достаточно больших значенияхn эмпирическая функция близка к теоретической, что следует из теоремы

Теорема. иимеет место

Таким образом, эмпирическая функция распределения выборки служит для оценки (приближенного выражения) теоретической функции распреде-ления генеральной совокупности.

Пример 3. Построить эмпирическую функцию распределения по данному распределению выборки.

	2	3	5
	5	20	25

Здесь п = 5 + 20 + 25 = 50, а

Тогда получим:

1. Если , то

2. Если , то

3. Если , то

4. Если , то

1

0,5

0,1

0 2 3 5 х

Тема 2 : Статистические оценки параметров распределения

2.1. Точечные оценки

Приближенные значения числовых параметров распределения называ-ются оценками. Различают точечные и интервальные оценки. Первые дают приближенные числовые значения изучаемого параметра , вторые – устанавливают вероятность покрытия этого параметра некоторым интер-валом, называемого доверительным.

К точечным оценкам параметров распределения случайной величины предъявляют следующие требования:

1. Состоятельности: Если точечная оценка параметра, то;

2. Несмещенности: , т.е. математическое ожидание оценкиравно оцениваемому параметру;

3. Эффективности: , т.е. дисперсия принимает минималь-ное значение.

Точечной оценкой для математического ожидания служит выборочное математическое ожидание:

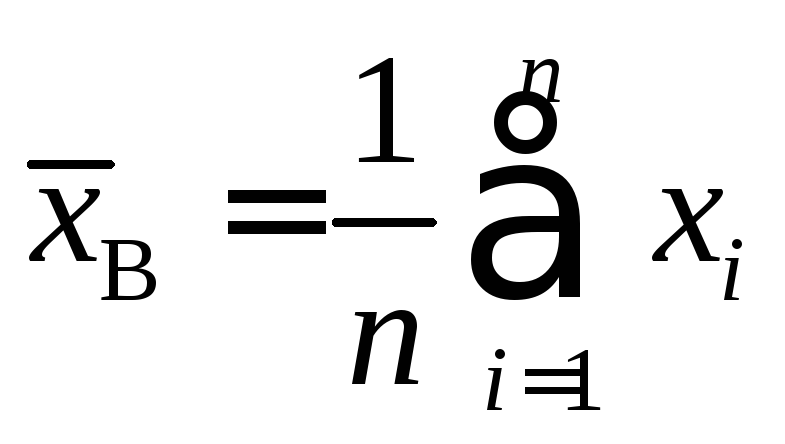, если все варианты различны,

а в противном случае  .

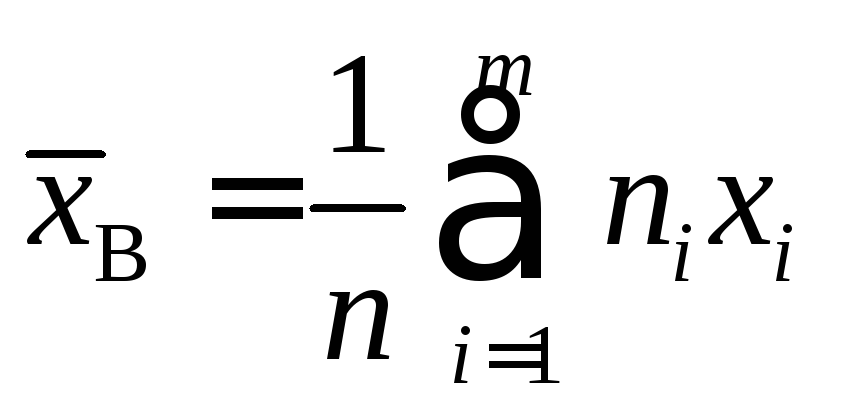Эта оценка удовлетворяет всем трём требованиям.

Точечной оценкой для дисперсии служит выборочная дисперсия

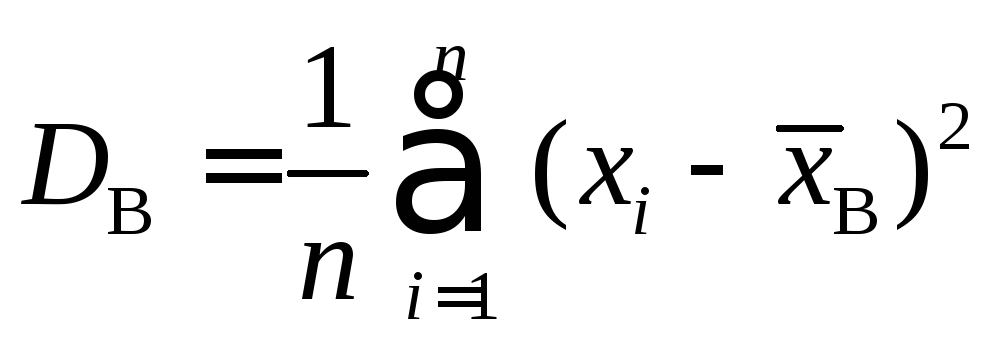или .

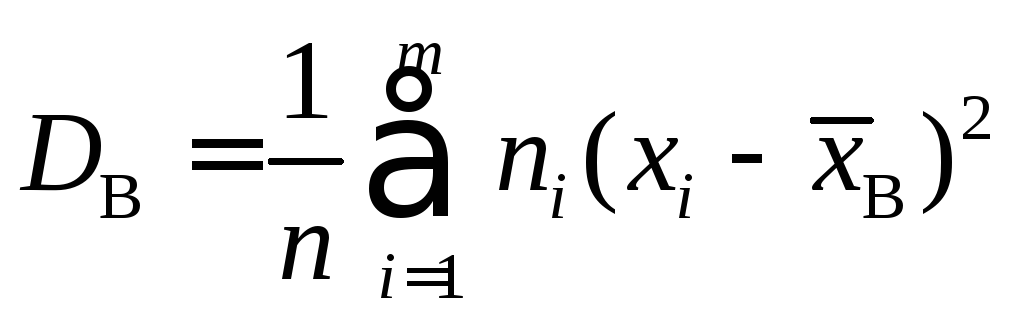Эта оценка является состоятельной и эффективной, но для нее, как можно показать, выполняется

,

т.е. данная оценка является смещенной.

Это можно устранить,если ввести исправленную дисперсию 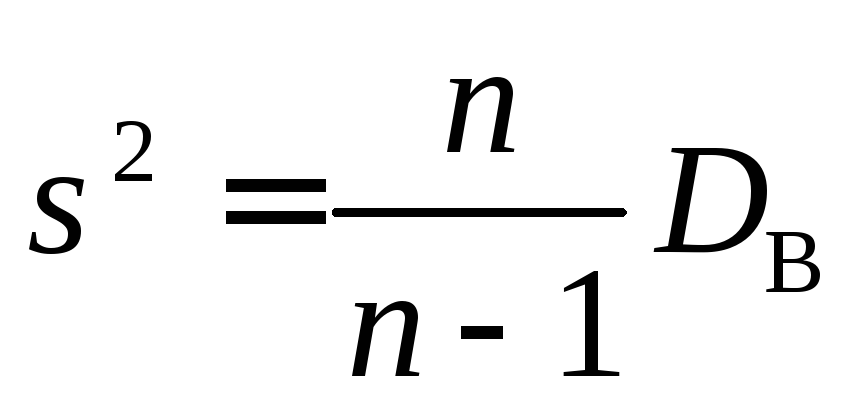, которая будет удовлетворять всем трём требованиям.

2.2. Интервальные оценки

Пусть для некоторого числового параметра из опыта получена несмещённая оценка. Оценим возможную при этом ошибку. Зададим некоторую вероятность(доверительная вероятность илинадёжность) и найдём такое число (точность оценки), для которого выполняется

или . (1)

Равенство (1) нужно понимать так: вероятность того, что интервал (доверительный интервал) покрывает параметрравна.

Ограничимся нахождением доверительного интервала для математи-ческого ожидания нормального распределения для двух случаев:

1. Известно среднее квадратическое отклонение , тогда

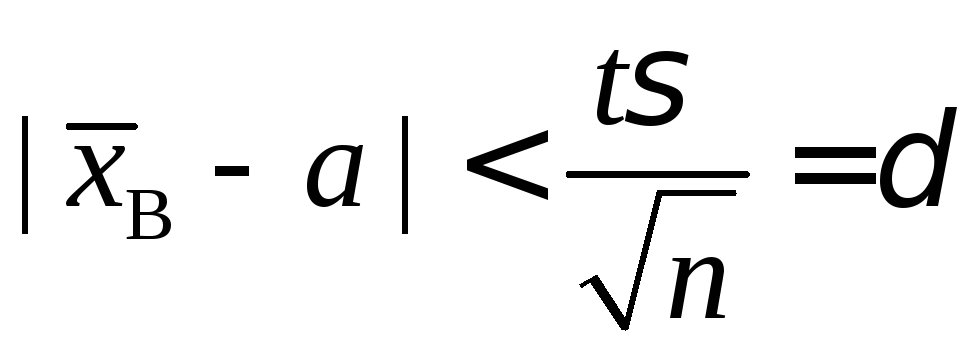или , (2)

где параметр t определяется по таблицам из условия

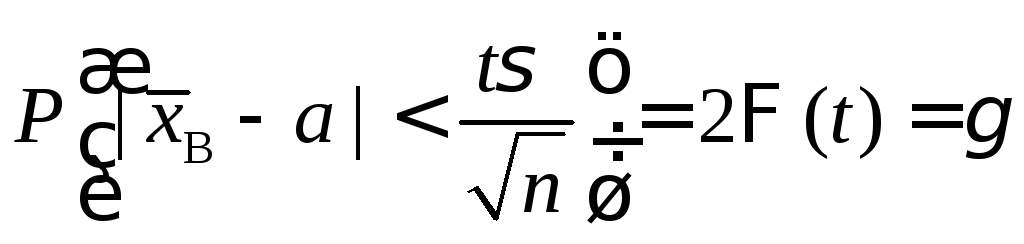или .

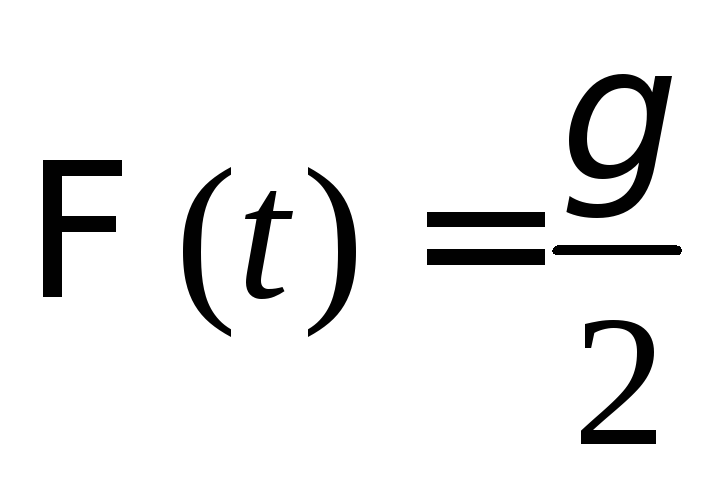Из оценки (2) можно сделать два вывода:

а) при возрастании объема выборки п величина убывает, следо-вательно, точность оценки увеличивается;

б) из увеличения надежности оценки следует увеличение параметраt и, соответственно, величины , следовательно, увеличение надежности уменьшает точность оценки.

Пример 4. Случайная величина Х имеет нормальное распределение с известным средним квадратическим отклонением =5. Найти доверитель-ный интервал для оценки неизвестного математического ожидания а по выборочным средним , если объем выборкип = 100 при заданной надежности

Из соотношения по таблице находим параметрt = 1,96. Тогда точность оценки

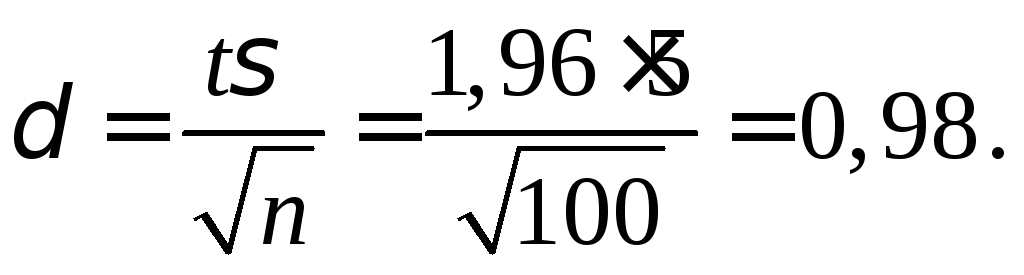
Таким образом, доверительный интервал или

Например, если найденное выборочное среднее , то с веро-ятностьюматематическое ожидание случайной величиныХ попадает в доверительный интервал .

2. Среднее квадратическое отклонение неизвестно. Тогда

,

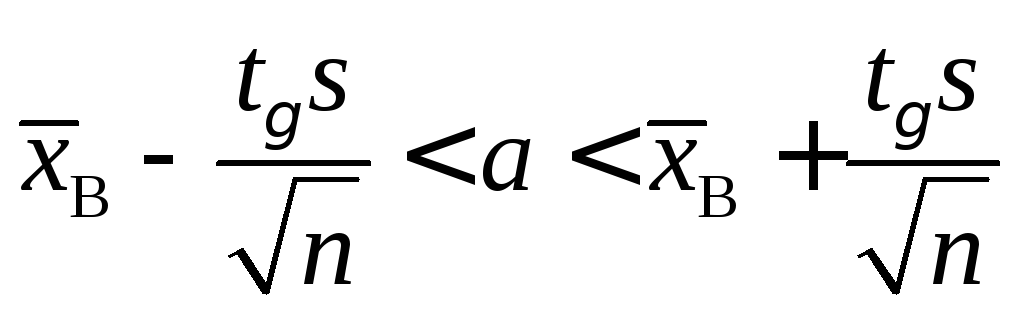где s  исправленное среднее квадратическое отклонение, а находится по таблицам критических значений так называемого распределения Стьюдента по значениямиn.

Пример 5. После проверки размера (в мм) выбранных 100 однотипных изделий получен вариационный ряд

	15,7	15,8	15,9	16,0	16,1	16,2
	2	18	30	40	8	2

Найти доверительный интервал для оценки неизвестного математичес-кого ожидания а при заданной надежности считая распреде-ление нормальным.

Найдем выборочное среднее и дисперсию

По таблице с учетом объема выборки п = 100 и заданной надеж-ности находим параметрt = 2,627. Тогда точность оценки

и доверительный интервал или