Лекция № 73

Тема 5 : Вычеты

5.1. Изолированные особые точки аналитической функции

Определение 1. Точки, в которых нарушается аналитичность функции , называютсяособыми.

Определение 2. Точка называется изолированной особой точкой, если существует такое число, что в кольцефункцияразлагается в ряд Лорана

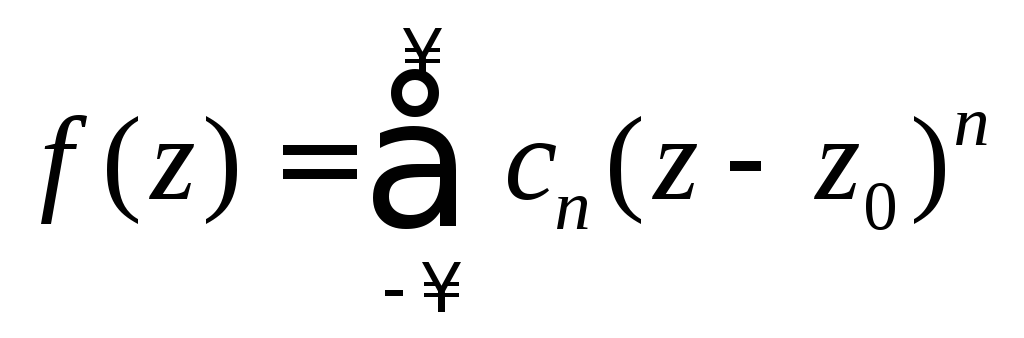. (1)

При этом возможны следующие случаи:

1. В разложении (2) нет членов с отрицательными показателями;

2. В разложении (2) есть конечное число членов с отрицательными по-казателями;

3. Разложение (2) содержит бесконечное число членов с отрицатель-ными показателями.

В этих случаях изолированная особая точка называется:

1 – устранимой; 2 – полюсом; 3 – существенно особой.

Если  полюс, то ряд Лорана имеет вид

.

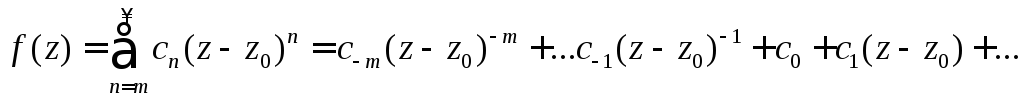В этом случае точка называетсяполюсом порядка т, а если , то полюс называетсяпростым.

В окрестности полюса порядка т функция имеет вид

,

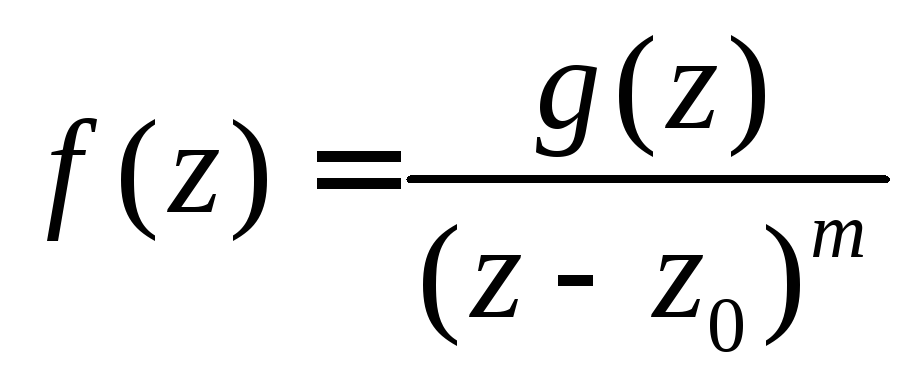где является аналитической функцией в окрестности полюса.

Легко заметить, что если  т-кратный нуль функции , то точкабудет полюсом порядкат для функции .

Если к плоскости комплексной переменной добавить бесконечно удалённую точку , то получим так называемуюрасширенную плоскость

комплексной переменной. Тогда подстановка 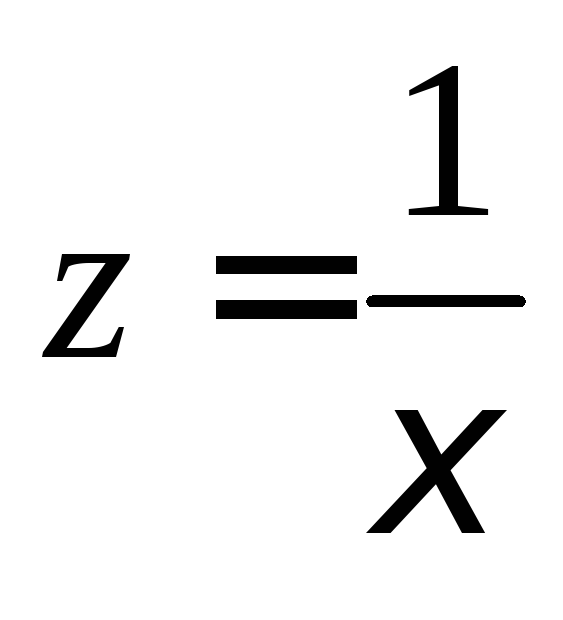приводит исследование функциив точкек исследованию функциив окрест-ности точки.

5.2. Определение вычета

Пусть  изолированная особая точка, тогда в её окрестности функ-цию можно представить в виде ряда

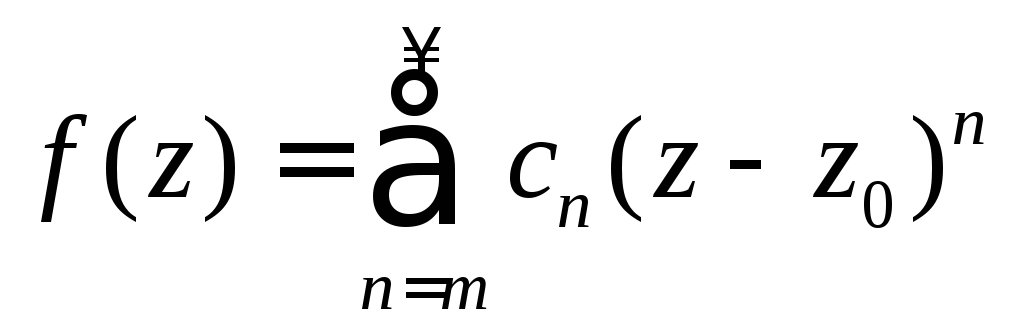, где .

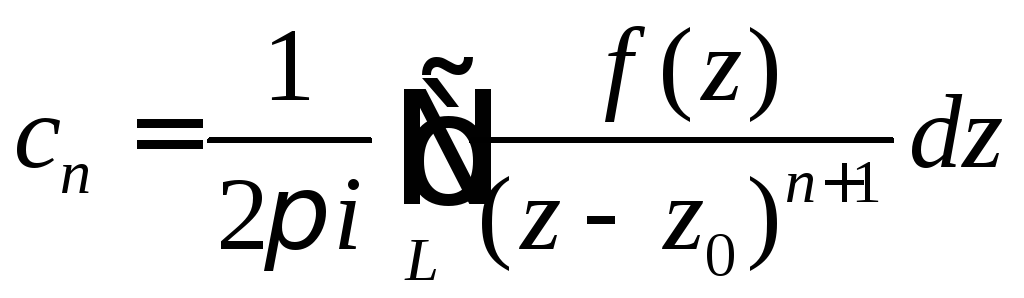Определение 3. Вычетом функции относительно особой точкиназывается коэффициент

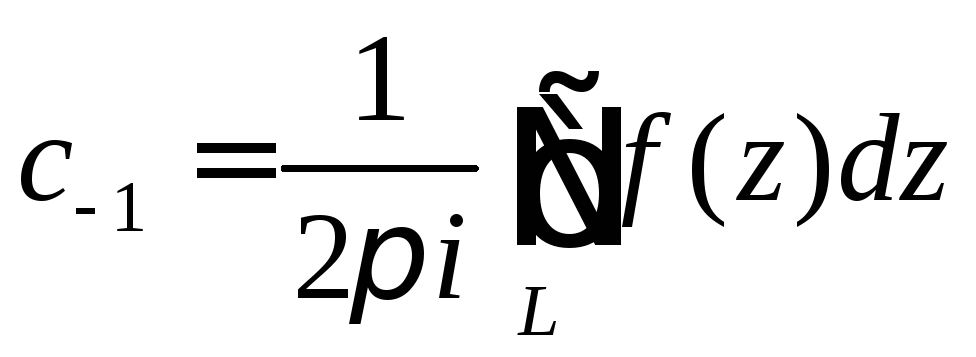
ряда Лорана и обозначается

или .

Из этого определения следует, что в точке, в которой функция является аналитической, или в устранимой особой точке вычет равен нулю.

Пусть  полюс, тогда возможны следующие случаи:

1.  простой полюс функции , тогда

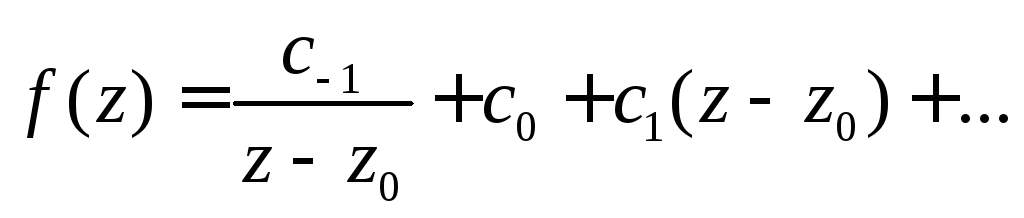
откуда

.

Переходя к пределу в этом равенстве при , получим

. (2)

Если 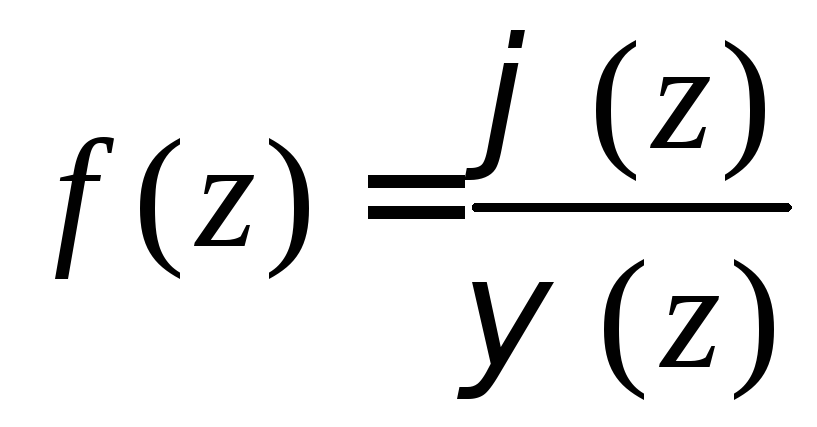, где- простой нуль функции. Тогда формула (3) примет вид

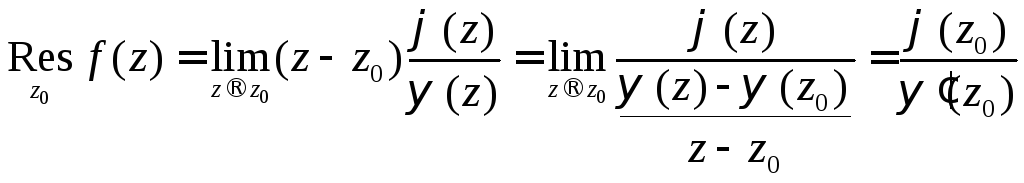. (3)

Пример 1. Найти вычет функции в точке.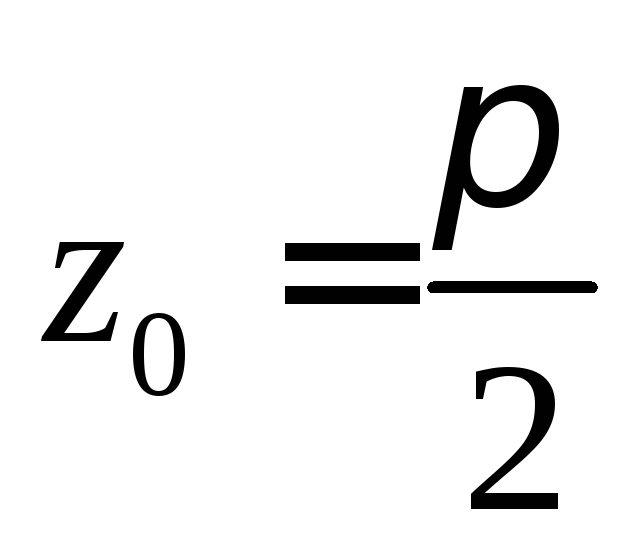

Используем формулу (3)

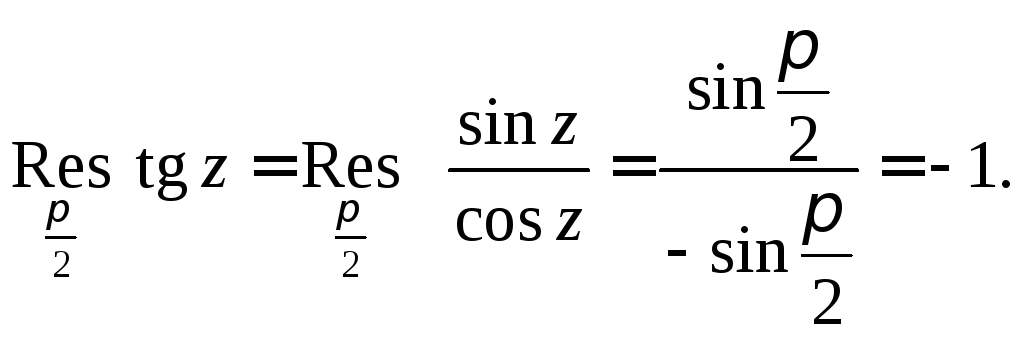
2. Если  полюс порядка т функции , тогда

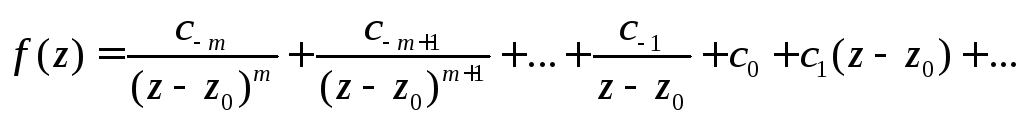
или

. (4)

Продифференцируем выражение (4) по раз:

.

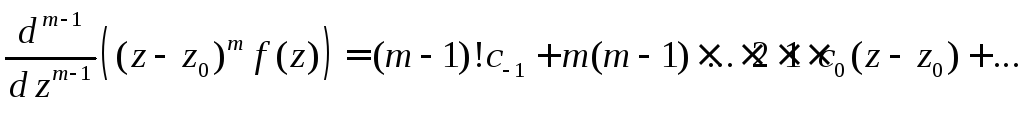Теперь перейдём к пределу при :

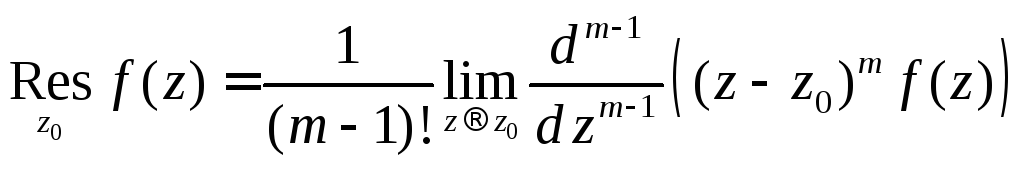. (5)

Пример 2. Найти вычеты функции .

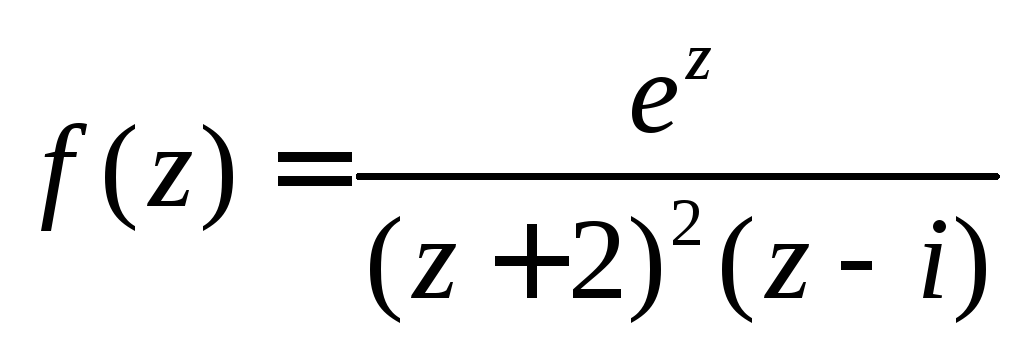Особыми точками для этой функции будут:  простой полюс и  полюс второго порядка. Воспользуемся соответственно форму-лами (3) и (5):

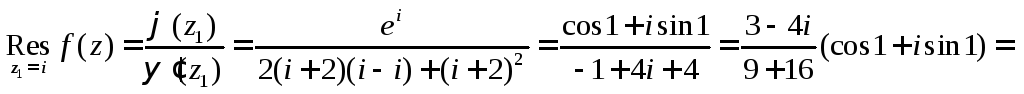
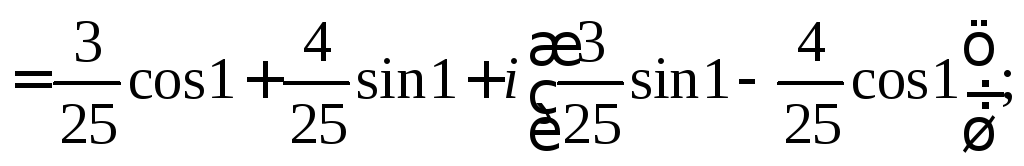
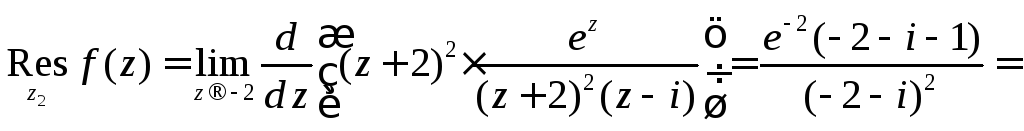
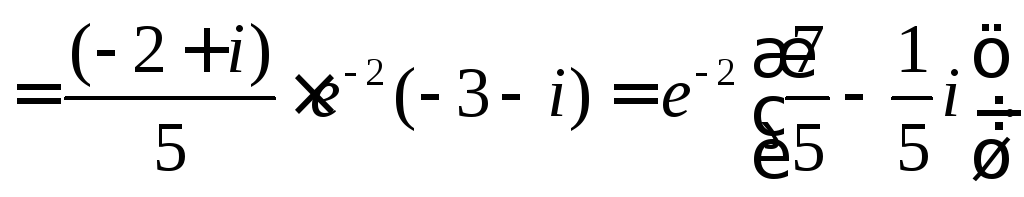
5.3. Основная теорема о вычетах

Теорема. Если функция однозначная и аналитическая в областивсюду, за исключением конечного числа изолированных особых точек, то

.

Пусть  непересекающиеся

окружности, а точки  их центры. L

Тогда внутри образовавшейся

многосвязной области функция

является аналитической, и по D

теореме Коши для сложного контура

получим

.

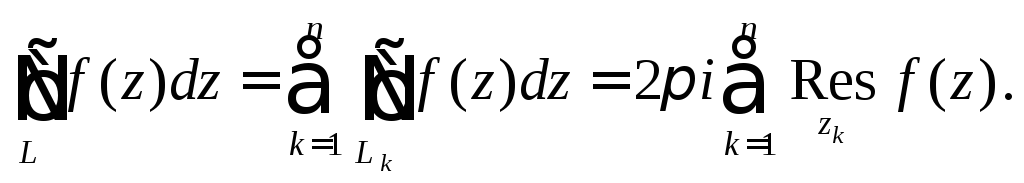5.4. Приложение вычетов к вычислению интегралов

С помощью вычетов можно вычислять интегралы следующего вида:

.

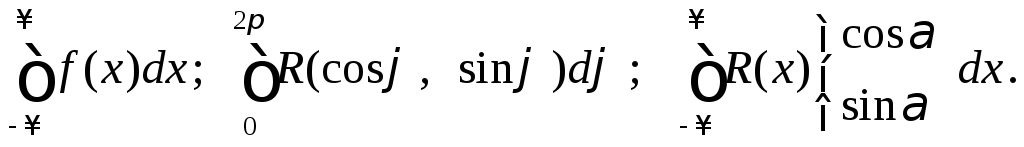Остановимся на первом интеграле.у

Рассмотрим аналитическое продолжение

функции . Пусть имеет в

верхней полуплоскости конечное число

особых точек: . При достаточно

большом R они все попадут во внутрь

полуокружности радиуса R. R О R х

Воспользуемся основной теоремой о вычетах

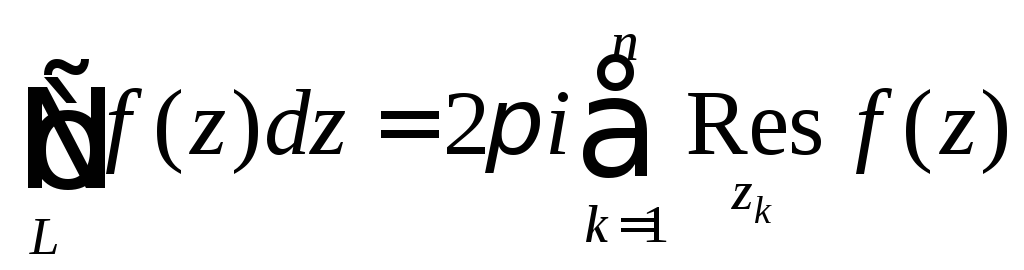
или

. (6)

Если 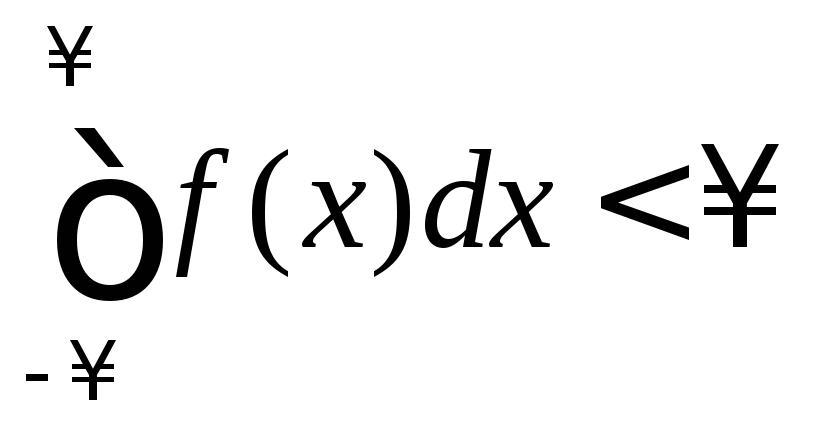, то должно выполняться условие,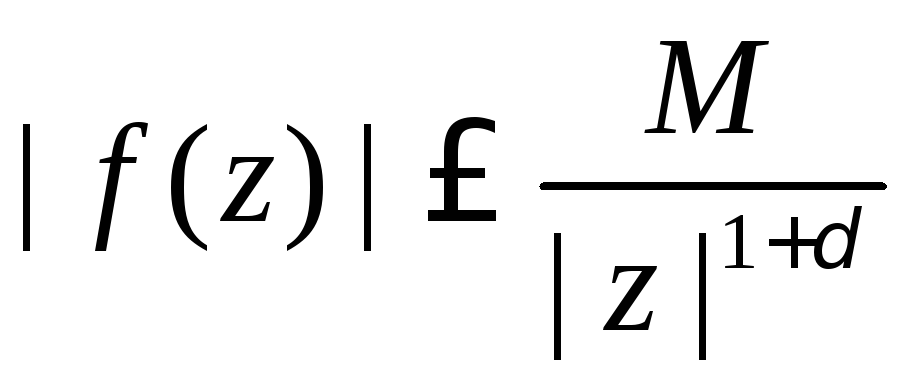

где .

Переходя к пределу при и учитывая, что

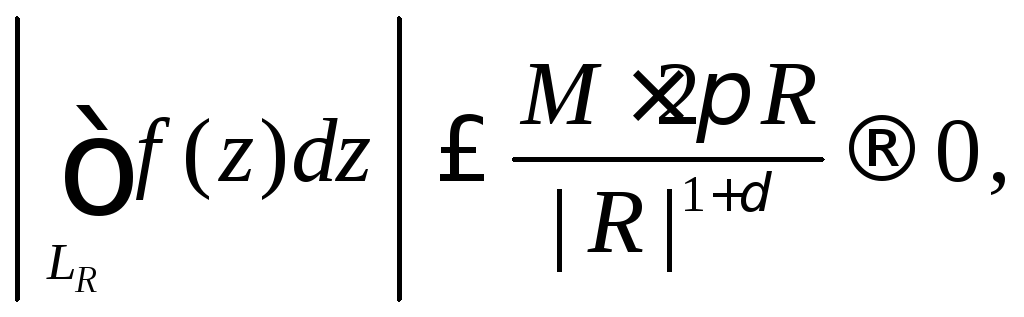
из формулы (6) получим

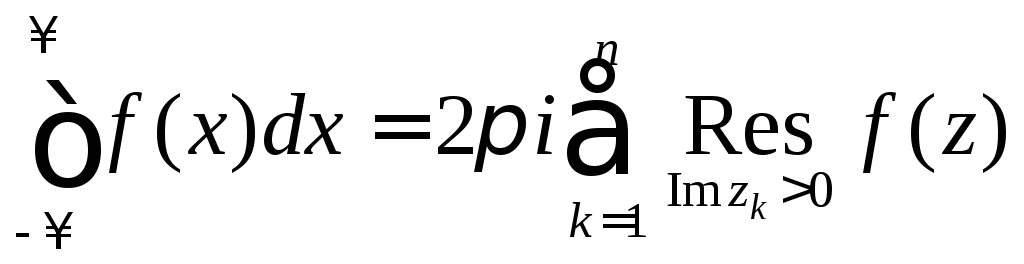. (7)

Пример 3. Вычислить интеграл .

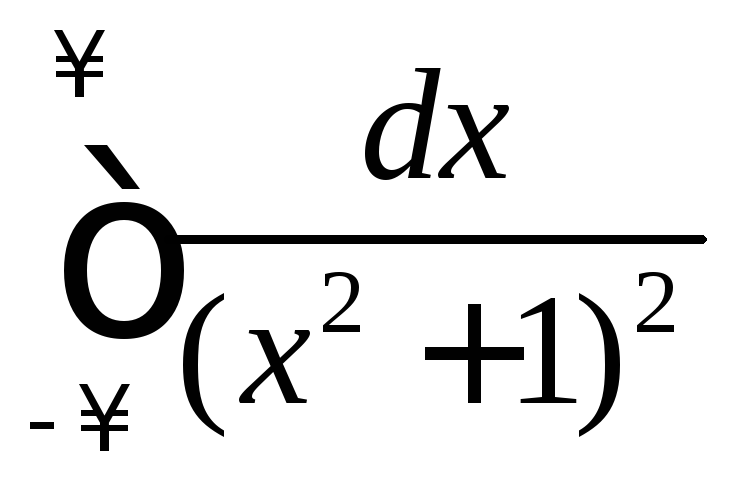Аналитическим продолжением подынтегральной функции является

,

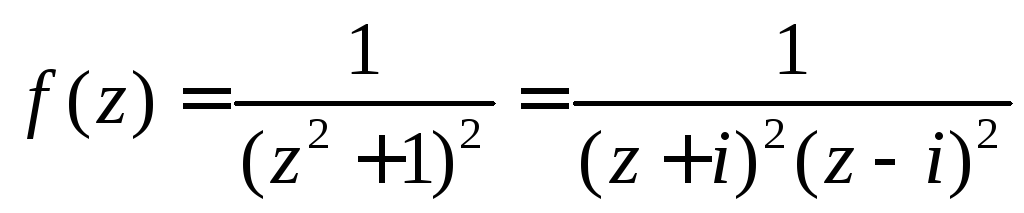у которой особой точкой, принадлежащей верхней полуплоскости, явля-ется . Вычислим вычет в этой точке по формуле (5)

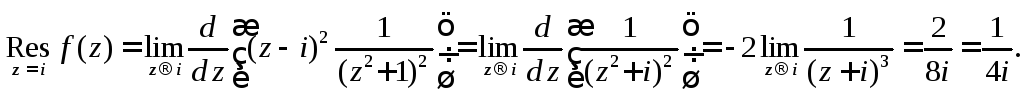
Тогда