6.2. Формула Гаусса  Остроградского

Теорема 1. Если функции являются непрерывными функциями вместе со своими частными производными первого порядка, то имеет место формула

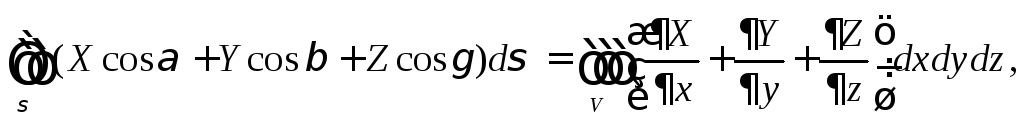(1)

где  направляющие косинусы единичного нормального вектора к поверхности, которая является границей областиV.

Замечание 1. Нетрудно заметить, что и тогда поток векторного поляопределяется по формуле

.

Пусть задано векторное поле . Рассмотрим некоторую точкуМ и окружим её поверхностью . Вычислим потокчерез эту поверхность. Если поле скоростей текущей жидкости, то возможны следующие случаи:

1.  количество втекающей жидкости равно количеству вытека-ющей жидкости;

2.  количество втекающей жидкости меньше вытекающей;

3.  количество втекающей жидкости больше вытекающей.

Во втором случае точка M называется источником, в третьем – стоком.

Рассмотрим отношение

,

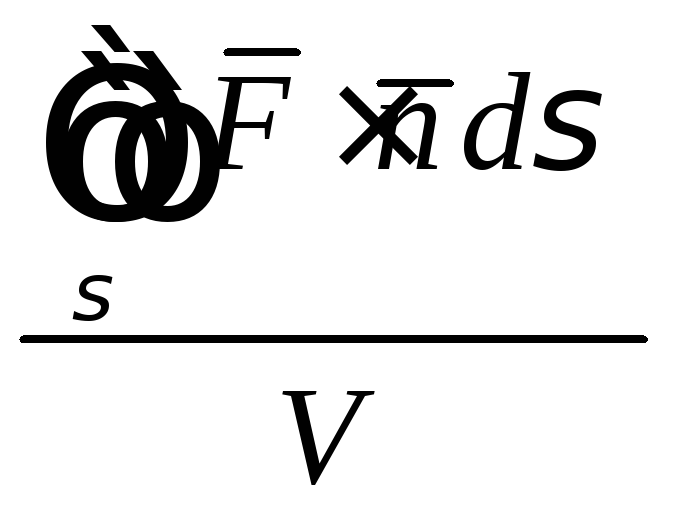где V  объём области с границей . Это отношение представляет собой среднюю мощность источников или стоков, находящихся внутри областиV.

Определение 2. Дивергенцией векторного поля в точкеМ назы-вается

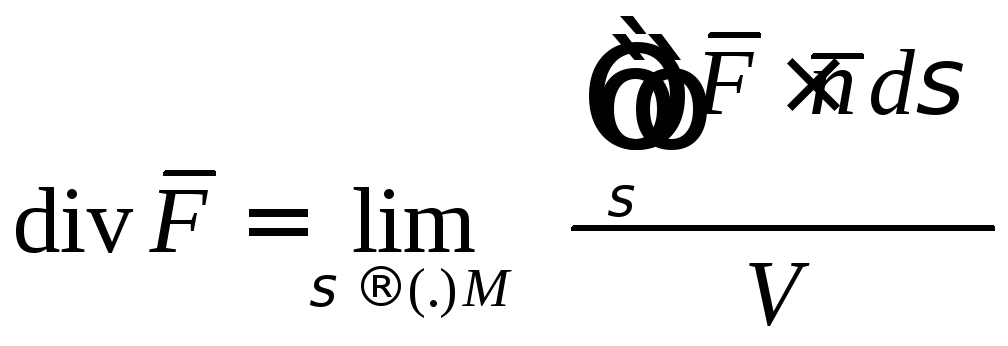. (2)

Таким образом, дивергенция в точке представляет собой мощность источника или стока, находящегося в этой точке.

Формулу (2) с учетом формулы (1) можно преобразовать к виду

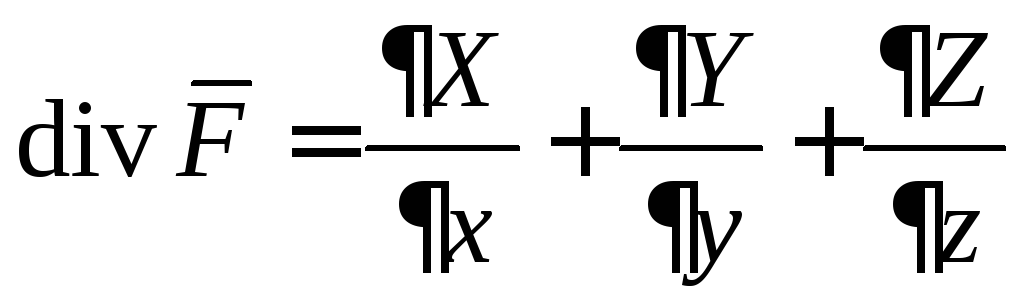. (3)

Замечание 2. В обозначении дивергенции формула (1) представляется в векторной форме

Определение 3. Если в каждой точке векторного поля выполняется условие

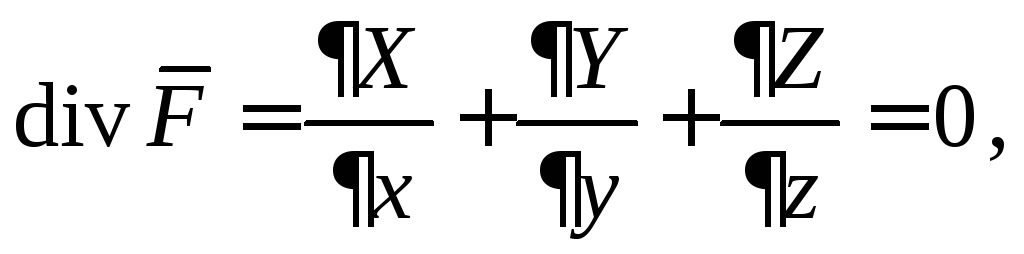
то такое поле называется соленоидальным.

Это поле, которое не имеет источников и стоков. Так, например, в рассмотренном выше примере поле

является соленоидальным.

6.3. Формула Стокса

Теорема 2. Если функции являются непрерывными функциями вместе со своими частными производными первого порядка, то имеет место формула

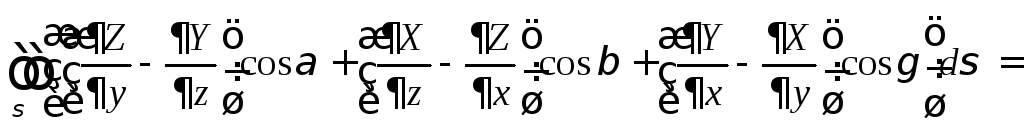
(4)

где L  граница поверхности .

Определение 4. Вектор

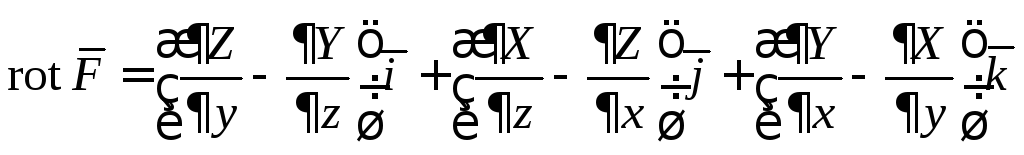
называется вихрем или ротором векторного поля .

Если поле скоростей текущей жидкости, то можно показать, чторавен удвоенной угловой скорости вращения бесконечно малой частицы в точкеМ, т.е. ротор характеризует вращательную способность векторного поля.

Замечание 3. В обозначении ротора формула (4) представляется в векторной форме

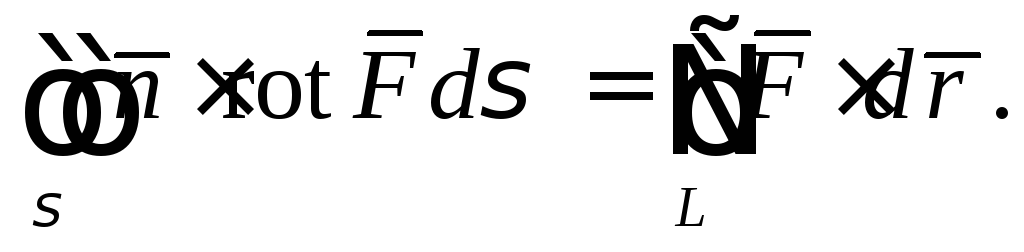
Определение 5. Значение интеграла

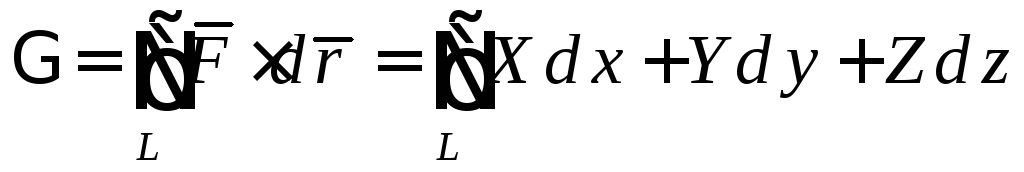
называется циркуляцией векторного поля вдоль контураL.

Аналогично, как и для плоского случая можно показать, что условие независимости криволинейного интеграла от пути интегрирования сводится к выполнению соотношения

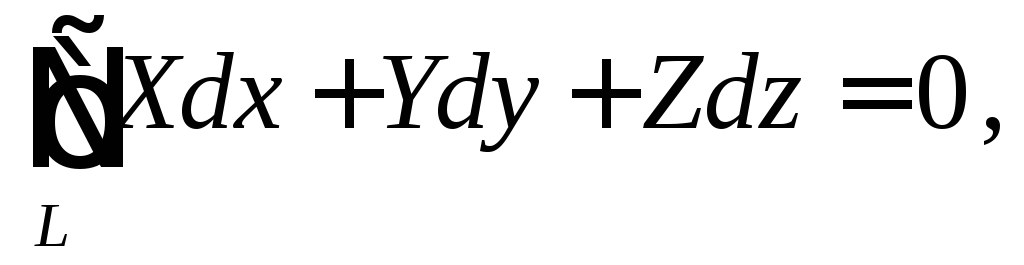(5)

где L - произвольный контур.

С учётом формулы Стокса условие (5) принимает вид

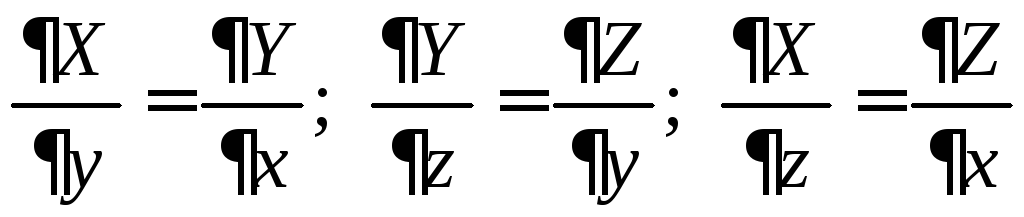, (6)

т.е. .

Это означает, что выражение является полным дифференциалом, т.е. существует такая функция, для которой выполняется, где

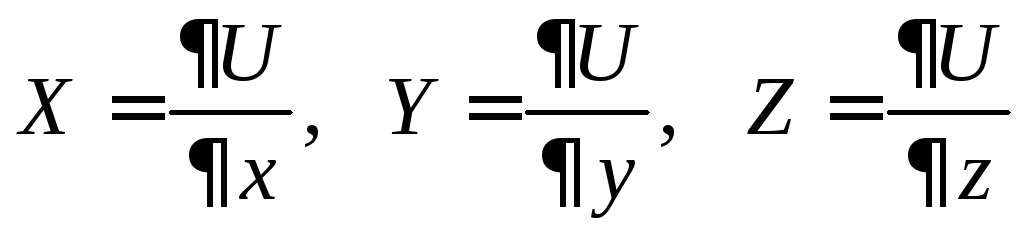
и

где  фиксированная точка,  текущая точка, а путь интегрирования выбирается произвольно.

Определение 6. Векторное поле, для которого выполняется условие ,называется потенциальным или безвихревым, а сама функция потенциалом.

Пример 2. Показать, что поле является потенциальным и найти его потенциал.

Проверим выполнение условий (6):

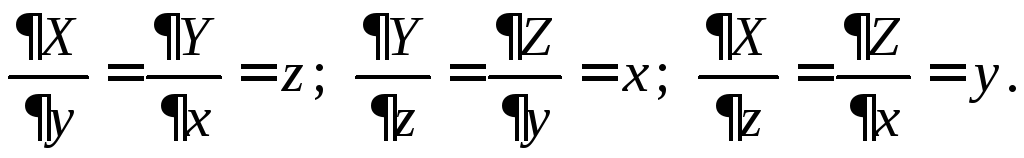
В качестве пути интегрирования выберем ломаную, звенья которой параллельны координатным осям, как показано на рисунке.

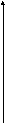z

y

x

Тогда

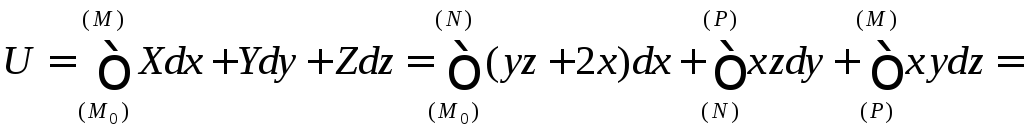
где .