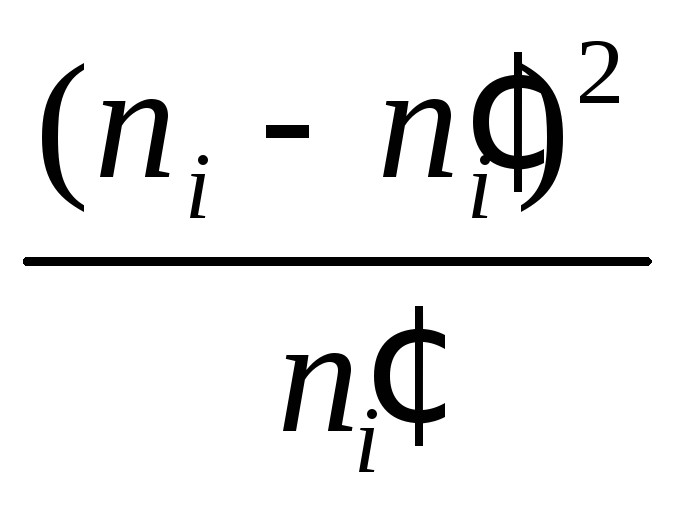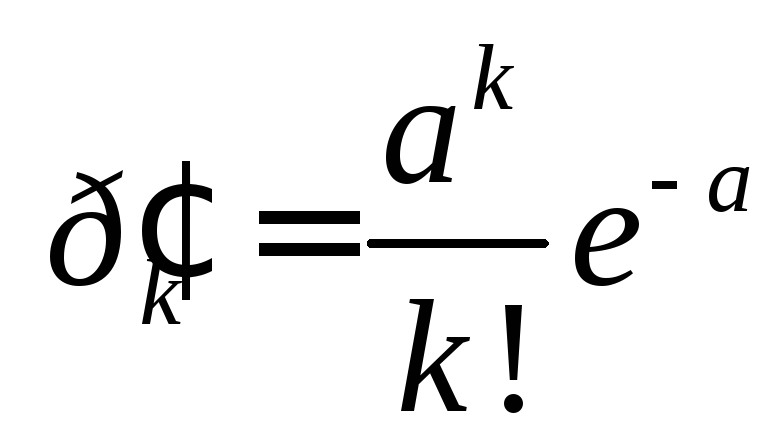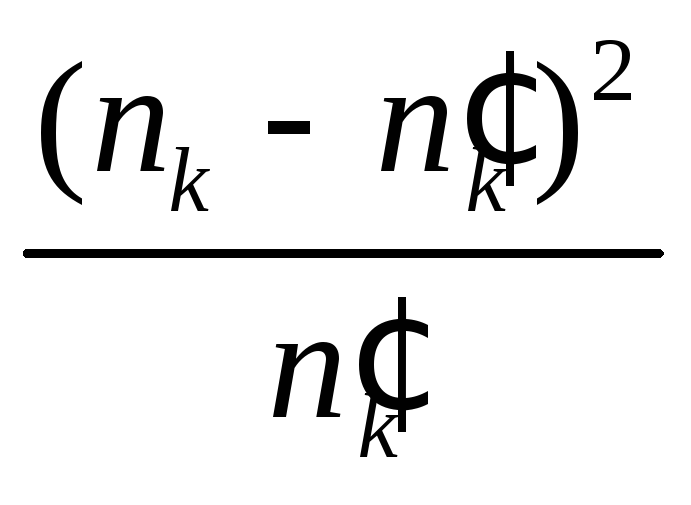3.2. Критерии проверки гипотезы

Таким образом, необходимы критерии, которые позволили бы иссле-довать, как согласуются наблюдаемые значения случайной величины X с выдвинутой гипотезой относительно её функции рас-пределения. Для этого используют специально подобранную случайную величину К, которую называют статистическим критерием.

Статистических критериев существует достаточно большое коли-чество и каждый из них имеет свое конкретное обозначение и предназ-начение. Например, критерий Фишера (F), критерий Стьюдента (Т), кри-терий Романовского (R), критерий Кочрена (G), критерий Вилкоксона (W) и т.д. Здесь мы пока будем использовать общее обозначение К.

После выбора конкретного критерия множество всех его возможных значений состоит из двух частей: в одной части содержатся значения критерия К, позволяющие принять выдвинутую гипотезу, а в другой  такие значения, при которых она отвергается. Область значений кри-терия К, при которых нулевая гипотеза отвергается, называется кри-тической областью. Область значений критерия К, при которых нулевая гипотеза принимается, называется областью принятия гипотезы.

Для проверки нулевой гипотезы по данным выборки определен-ным способом вычисляют случайную величину называемую наблю-даемым значением критерия. Если наблюдаемое значение критерия принадлежит критической области, то нулевая гипотеза отвергается, а если принадлежит области принятия решения – гипотеза принимается.

Критическими точками называют точки, отделяющие критичес-кую область от области принятия решения.

Если критическая точка одна, то имеем одностороннюю критичес-кую область  правостороннюю при и левостороннюю при Если критических точек две, то имеем двустороннюю крити-ческую область, определяемую неравенствами и где

Для определенности приведем алгоритм нахождения правосторонней критической области, определяемой неравенством :

 задаем уровень значимости ;

 по таблицам, имеющимся для каждого критерия, находим крити-ческую точку такую, чтобы. ;

 по выборке находим наблюдаемое значение критерия ;

 сравниваем и  если , то нулевая гипотеза отвергается, если же , то гипотезу принимаем.

Замечание. Наблюдаемое значение критерия может быть больше не потому, что гипотезаневерна, а по техническим причинам (ошибки вычислений, недостаточный объем выборки, не вполне совер-шенная технология выборки и т.п.). В этом случае мы совершаем ошибку первого рода – ее вероятность мала и равна уровню значимости .

3.3. Критерий согласия Пирсона

Критерии проверки гипотезы о предполагаемом законе неизвестного распределения называются критериями согласия. В основе их построения лежит исследование величины отклонения теоретической функции рас-пределения от эмпирической функции распределения

Наиболее распространённой такой величиной является критерий со-гласия „хи-квадрат”, введённый Пирсоном

. (3.1)

Множество значений случайной величиныХ разбивается на т полу-интервалов без общих точек

. . . . .

[ [ [ [ [

Здесь  частота появления признака, принадлежащего интервалу . Очевидно, что объём выборки .

Теоретические частоты , соответствующие эмпирическим, вычис-лены по предполагаемому закону распределения (гипотезе), для них также должно выполняться равенство

Величина является случайной величиной, при этом ее распреде-ление не зависит от функции распределения случайной величиныX и стре-мится при к так называемому-распределению сстепенями свободы, гдеr  число параметров теоретического закона.

Пусть эмпирическое распределение (выборка) задано в виде интерваль-ного вариационного ряда равноотстоящих вариант с шагом h

			…
			…

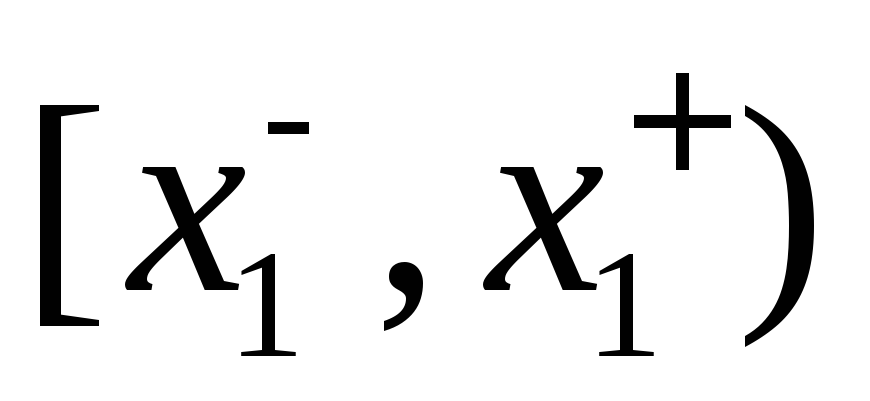
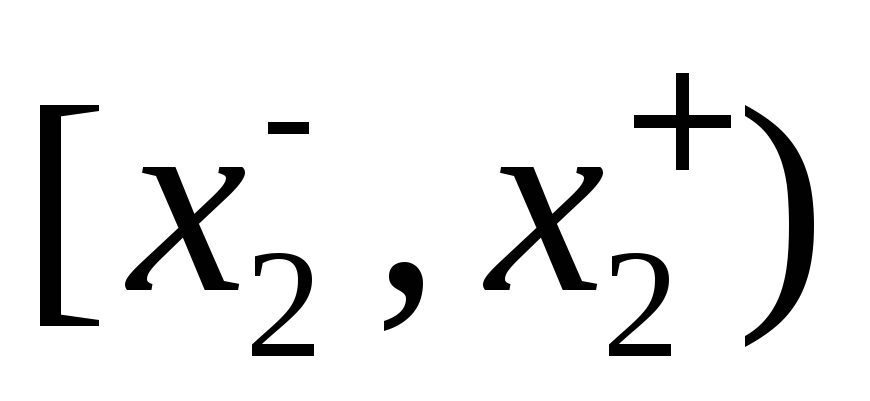
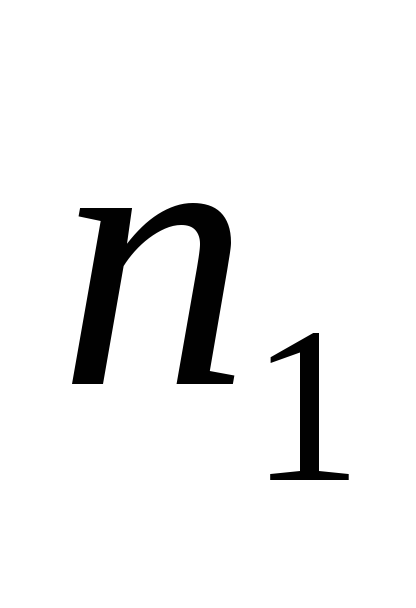
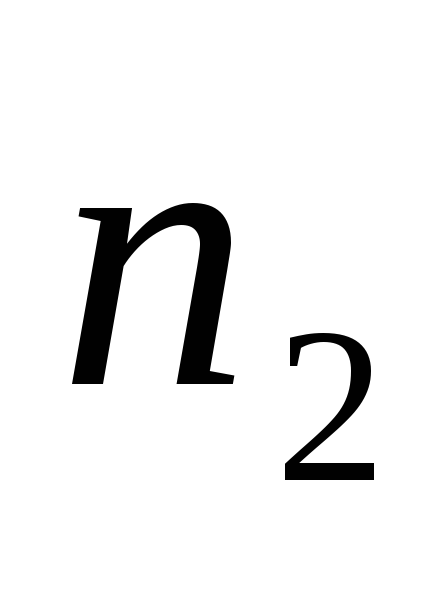
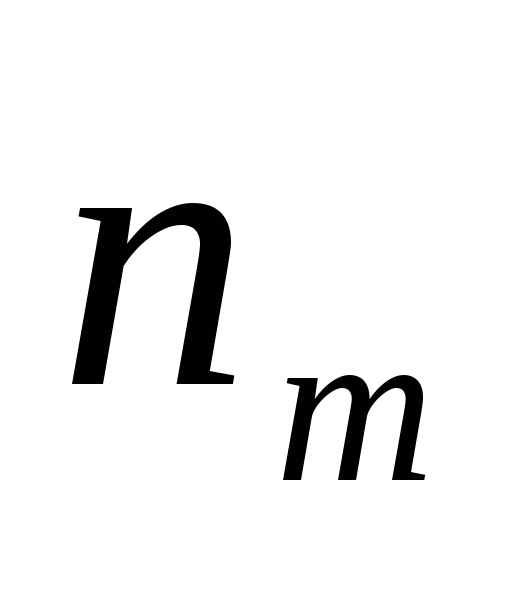
Рассмотрим применение критерия Пирсона для проверки гипотез о нормальном распределении изучаемой случайной величины и распреде-лении Пуассона.

3.3.1. Нормальное распределение

1. Вычисляем выборочное среднее где,

и исправленное выборочное среднее квадратическое отклонение

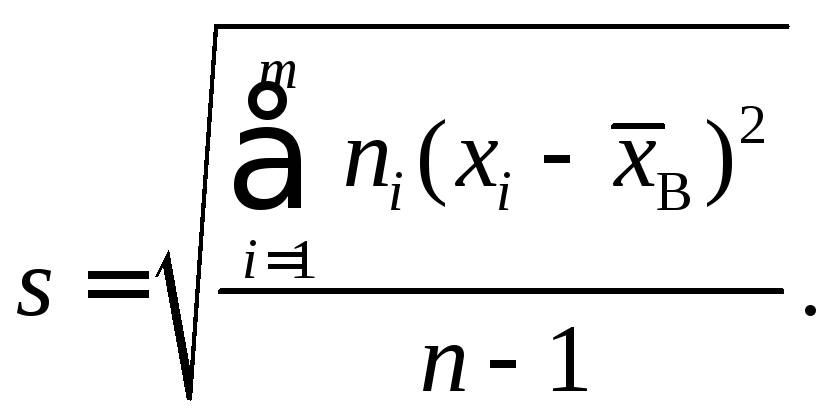
2. Определяем теоретические частоты , считая закон распределения нормальным, т.е.

, (3.2)

где от исходных интервалов вариационного ряда переходим к нормированным интервалампо формулам

,

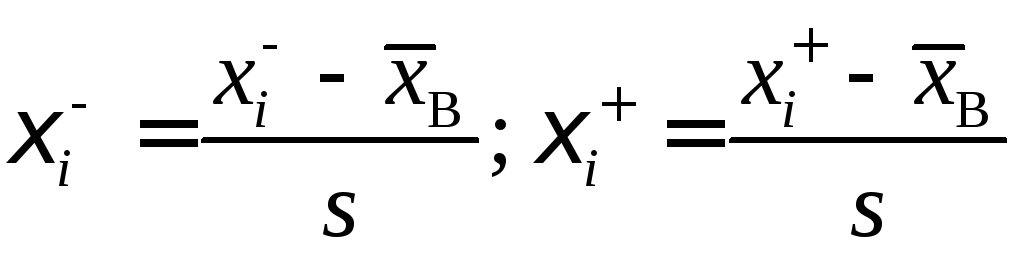а значения функции Лапласа берутся из таблицы в Приложении2, причем полагаем, что крайние значения и

3. По формуле (3.1) вычисляем величину .

4. Определяем число степеней свободы  для нормального распреде-ления

5. По таблице (прил. 6) критических точек распределения , по за-данному уровню значимостии числу степеней свободыk находим критическую точку . Если , то гипотеза о нормаль-ном распределении принимается, т.е. эмпирические и теоретические частоты различаются незначительно. В противном случае гипотеза отвергается.

Пример 3.1. Проверить, согласуются ли данные таблицы с предполо-жением, что рост мужчины является нормально распределённой случайной величиной, приняв уровень значимости

156	11		-2,27	-0,5000	-0,4884	0,0116	11,6	0,031
160	26	-2,27	-1,76	-0,4884	-0,4608	0,0276	27,6	0,093
164	65	-1,76	-1,26	-0,4608	-0,3962	0,0646	64,6	0,002
168	120	-1,26	-0,76	-0,3962	-0,2764	0,1198	119,8	0,000
172	181	-0,76	-0,26	-0,2764	-0,1026	0,1738	173,8	0,298
176	201	-0,26	0,25	-0,1026	0,0987	0,2013	201,3	0,000
180	170	0,25	0,75	0,0987	0,2734	0,1747	174,7	0,126
184	120	0,75	1,25	0,2734	0,3943	0,1209	120,9	0,007
188	64	1,25	1,75	0,3943	0,4599	0,0656	65,6	0,039
192	28	1,75	2,26	0,4599	0,4881	0,0282	28,2	0,001
196	14	2,26		0,4881	0,5000	0,0119	11,9	0,371
Итого	1000					1,0000	1000	0,969

По данным таблицы вычисляем и, норми-руем интервалы и находим теоретические частотыпо формуле (3.2).

Таким образом, . По уровню значимости и числу степеней свободыпо таблице (прил.6) критических точек распределения находим=20,1. Так как , то гипотеза о нормальном распределении принимается.

3.3.2. Распределение Пуассона

1. Поскольку распределение Пуассона является дискретным, то k-ому интервалу вариационного ряда (выборки) ставимвсоответствиеслучайнуювеличинуk  1= 0, 1, 2, … , m  1.

2. Вычисляем выборочное среднее 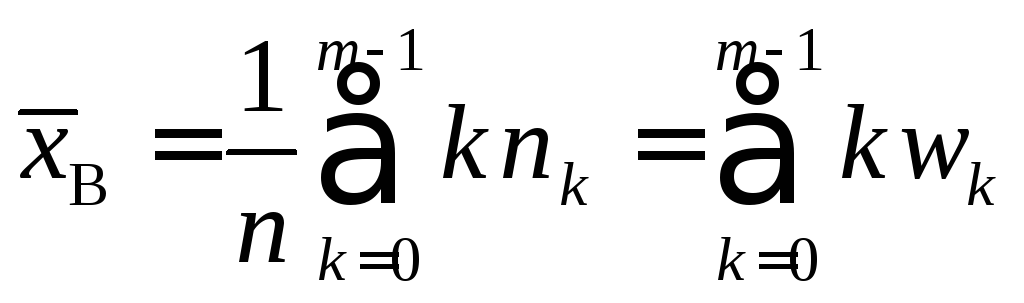, которое,

как следует из теории, для распределения Пуассона должно быть дос-таточно близким к дисперсии.

3. По формуле Пуассона определяем теоретические частоты

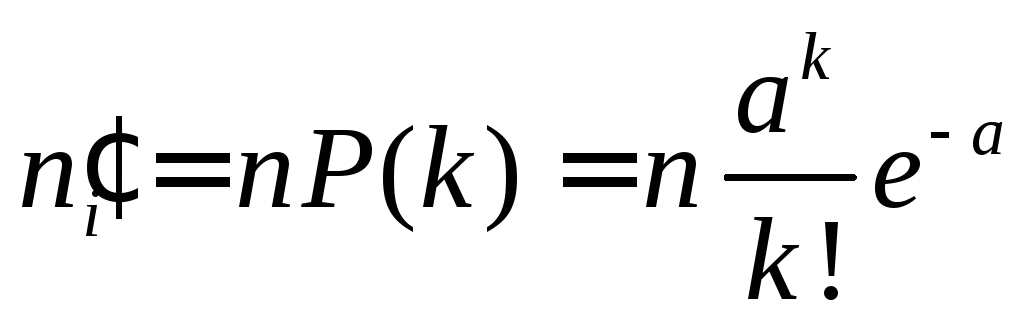, (3.3)

где полагаем , а искомые вероятностиможно получить также и из таблицы распределения Пуассона (прил.3).

4. По формуле (3.1) вычисляем величину .

5. Определяем число степеней свободы для распределения Пуассона

6. По таблице (прил.6) критических точек распределения , по за-данному уровню значимостии числу степеней свободыk находим критическую точку . Если , то гипотеза о распре-делении Пуассона принимается, т.е. эмпирические и теоретические частоты различаются незначительно. В противном случае гипотеза отвергается.

Пример 3.2. Проверить, согласуются ли данные таблицы с гипотезой о том, что рост мужчины является случайной величиной, распределённой по закону распределения Пуассона, приняв уровень значимости

Переходим к дискретной случайной величине и вычисляем выбо-рочное среднее. Далее по формуле (3.3) или по таблице (прил.3) распределения Пуассона (графа ) определяем теоретические вероятностии теоретические частотыс округлением к большему числу.

156	11	0,011	0	0,0077	7	2,29
160	26	0,026	1	0,0337	34	1,88
164	65	0,065	2	0,0842	85	4,71
168	120	0,120	3	0,1404	141	3,13
172	181	0,181	4	0,1755	176	0,14
176	201	0,201	5	0,1755	176	3,55
180	170	0,170	6	0,1462	147	3,60
184	120	0,120	7	0,1044	104	2,46
188	64	0,064	8	0,0653	66	0,06
192	28	0,028	9	0,0363	37	2,19
196	14	0,014	10	0,0181	19	1,32
Итого	1000	1,000		0,9873	992
	0	0,000	11		8	8,00
Итого	1000	1,000			1000	33,32

Поскольку 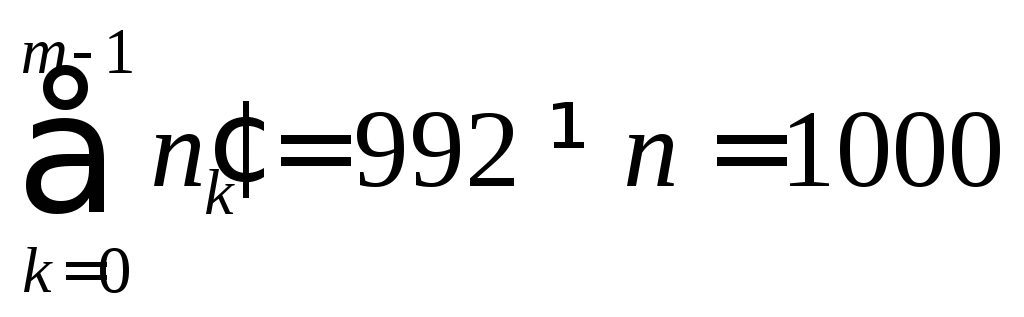, то можно добавить в постро-енную таблицу еще одну строку сдля выравнивания суммы теоретических частот.

Вычисляем . По уровню значимости и числу степеней свободыпо таблице (прил.6) критических точек распределения находим=18,3. Так как , то гипотеза о распределении Пуассона отвергается.