3.4. Критерий согласия Романовского
Критерий согласия
Романовского полностью использует
вычислитель-ную часть критерия Пирсона
и является хорошим дополнением к этому
критерию, не требующим существенных
дополнительных расчетов.
Его суть сводится к вычислению одной величины
где 
расчетное значение
критерия согласия Пирсона, а k
число
степеней свободы. Если значение R < 3, то результаты испытаний не противоречат выдвигаемой гипотезе. Например, для проанализированных выше гипотез (п.3.3.1 и п.3.3.2) имеем
что подтверждает сделанные ранее выводы.
4. Элементы теории корреляции
4.1. Статистические зависимости
Во многих задачах требуется установить и оценить зависимость изучаемой случайной величины Y от другой случайной величины Х.
Две случайные величины могут быть связаны определённой зависимостью, которую принято называть статистической, или быть независимыми.
Определение 4.1. Статистической называется зависимость, при которой изменение одной случайной величины Х влияет на распределение другой случайной величины Y. Если при этом изменяется еще и среднее значе-ние случайной величины Y, то такая зависимость называется корреля-ционной.
Например, пусть Х сумма затрат на подготовку лавы, а Y уровень добычи угля. При одинаковых затратах на подготовку лав добыча угля будет отличаться, т.е. случайная величина Y не является функцией от Х. Это можно объяснить влиянием ряда случайных факторов (глубиной залегания пласта, его мощностью, сортностью угля и т.п.). Тем не менее, средняя величина добычи угля является функцией от суммы затрат, т.е. случайные величины Y и Х связаны корреляционной зависимостью.
4.2. Линейная регрессия
Определение 4.2. Выборочным уравнением линейной регрессии случай-ной величины Y на Х называется уравнение вида
(4.1)
Уравнение (4.1) часто
называют просто уравнением линейной
регрессии, а угловой коэффициент
выборочным
коэффициентом регрессии.
Для отыскания выборочного уравнения регрессии воспользуемся методом наименьших квадратов, т.е. мы должны минимизировать функцию суммы квадратов отклонений
Для отыскания
минимума функции
приравняем нулю обе частные производные:
Выполнив элементарные
преобразования, получим систему двух
линейных уравнений относительно
иb:
(4.2)
откуда легко находим искомое.
Замечание 2. На практике при составлении системы (4.2) для избежания вычислений с большими числами обычно делают усреднение, т.е. все коэффициенты системы (4.2) делятся на п
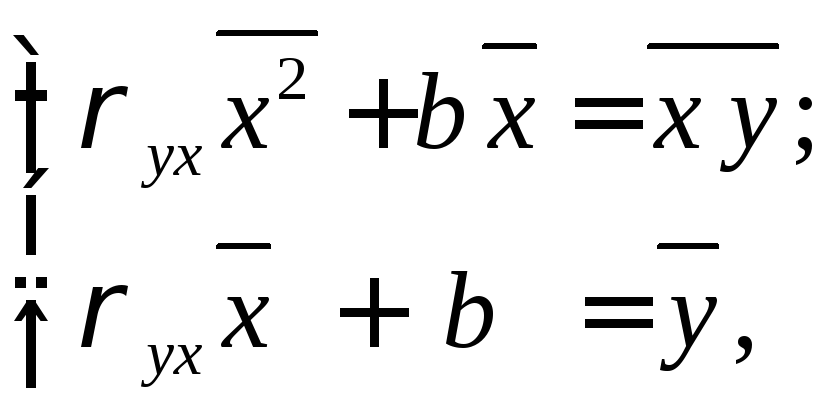(4.3)
переходя к выборочным средним
Тогда решение системы (4.2) можно записать в виде:
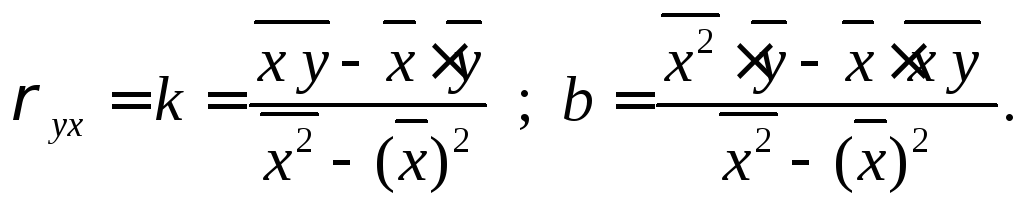(4.4)
Пример 4.1. Найти выборочное уравнение линейной регрессии случайной величины Y на случайную величину Х по данным 10 наблюдений:
|
п |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
X |
1,5 |
2,5 |
3,0 |
3,5 |
5,0 |
6,0 |
7,5 |
8,5 |
9,0 |
9,5 |
|
Y |
11,0 |
10,0 |
9,0 |
8,0 |
7,5 |
7,5 |
7,0 |
6,5 |
5,5 |
5,0 |
Составим расчетную таблицу:
|
|
|
|
|
|
1,5 |
11,0 |
2,25 |
16,50 |
|
2,5 |
10,0 |
6,25 |
25,00 |
|
3,0 |
9,0 |
9,00 |
27,00 |
|
3,5 |
8,0 |
12,25 |
28,00 |
|
5,0 |
7,5 |
25,00 |
37,50 |
|
6,0 |
7,5 |
36,00 |
45,00 |
|
7,5 |
7,0 |
56,25 |
52,50 |
|
8,5 |
6,5 |
72,25 |
55,25 |
|
9,0 |
5,5 |
81,00 |
49,50 |
|
9,5 |
5,0 |
90,25 |
47,50 |
|
|
|
|
|
|
|
|
|
|
По формулам
(4.4)
получим
и
.
Таким образом,
линейная регрессия имеет вид
.
Проверим, насколько
хорошо полученные результаты согласуются
с наблюдаемыми данными. Найдем отклонения
|
|
|
|
|
|
1,5 |
10,23 |
11,0 |
-0,77 |
|
2,5 |
9,62 |
10,0 |
-0,38 |
|
3,0 |
9,31 |
9,0 |
0,31 |
|
3,5 |
9,00 |
8,0 |
1,00 |
|
5,0 |
8,08 |
7,5 |
0,57 |
|
6,0 |
7,46 |
7,5 |
-0,04 |
|
7,5 |
6,53 |
7,0 |
-0,47 |
|
8,5 |
5,92 |
6,5 |
-0,58 |
|
9,0 |
5,61 |
5,5 |
0,11 |
|
9,5 |
5,30 |
5,0 |
0,30 |
Как видим из построенной таблицы, не все отклонения достаточно малы. Эти расхождения объясняются недостаточным количеством наблю-даемых данных, т.е. небольшим размером выборки..