
- •Теория вероятностей и математическая статистика
- •Теория вероятностей
- •1. Общие понятия
- •1.1. Предмет теории вероятностей
- •1.2. Пространство элементарных событий
- •1.3. Операции над событиями
- •1.4. Статистический подход к понятию вероятности
- •1.5. Элементы комбинаторики
- •1. Перестановки.
- •2. Сочетания.
- •3. Размещения.
- •1.6. Классическое определение вероятности
- •1.7. Аксиоматическое определение вероятности
- •2. Основные теоремы теории вероятностей
- •2.1. Теорема умножения вероятностей
- •2.2. Теорема сложения вероятностей
- •2.3. Формула полной вероятности
- •2.4. Формула Бейеса
- •3. Повторение испытаний
- •3.1. Независимые испытания. Формула Бернулли
- •3.2. Локальная теорема Муавра – Лапласа
- •3.3. Интегральная теорема Лапласа
- •3.4. Теорема Пуассона
- •3.5. Вероятность отклонения частоты от постоянной вероятности в независимых испытаниях
- •4. Случайные величины и функции распределения
- •4.1. Случайные величины
- •4.2. Функция распределения вероятностей для дискретной св
- •4.3. Функция распределения вероятностей для непрерывной св.
- •4.4. Функция плотности распределения вероятностей
- •5. Числовые характеристики случайных величин
- •5.1. Математическое ожидание случайной величины
- •5.2. Дисперсия и среднее квадратическое отклонение св
- •5.3. Моменты и другие числовые характеристики случайной величины
- •6. Основные законы распределения случайных величин
- •6.1. Законы распределения дискретных случайных величин
- •6.1.1. Биномиальное распределение
- •6.1.2. Распределение Пуассона
- •6.1.3. Геометрическое распределение
- •6.2. Законы распределения непрерывных случайных величин
- •6.2.1. Равномерное распределение
- •6.2.2. Показательное распределение
- •6.2.3. Нормальное распределение
- •7. Закон больших чисел
- •7.1. Неравенства Чебышева
- •7.2. Теорема Чебышева
- •8. Многомерные случайные величины
- •8.1. Многомерные случайные величины и их функции распределения
- •X и y независимые случайные величины.
- •8.2. Вероятность попадания двумерной случайной величины
- •8.3. Числовые характеристики двумерной случайной величины
- •Математическая статистика
- •1. Статистические законы распределения выборки
- •1.1. Вариационный ряд
- •1.2. Полигон и гистограмма
- •1.3. Эмпирическая функция распределения
- •2. Статистические оценки параметров распределения
- •2.1. Точечные оценки
- •2.2. Интервальные оценки
- •2.3. Оценка вероятности появления события через его частоту
- •3. Проверка статистических гипотез.
- •3.1. Статистические гипотезы
- •3.2. Критерии проверки гипотезы
- •3.3. Критерий согласия Пирсона
- •3.4. Критерий согласия Романовского
- •4. Элементы теории корреляции
- •4.1. Статистические зависимости
- •4.2. Линейная регрессия
- •4.3. Корреляционная таблица
- •4.4. Выборочный коэффициент корреляции
- •Литература
- •С о д е р ж а н и е
3.2. Локальная теорема Муавра – Лапласа
При больших значениях n формулу (3.1) использовать затруднительно. Поэтому возникает вопрос о замене её некоторой асимптотической формулой, т.е. приближенной, справедливой при больших п.
Теорема 3.1.
Если вероятность появления события А
в каждом из независимых испытаний
постоянна и равна р,
то вероятность
![]() при большихп
приближенно равна значению функции
при большихп
приближенно равна значению функции
 ,
где
,
где
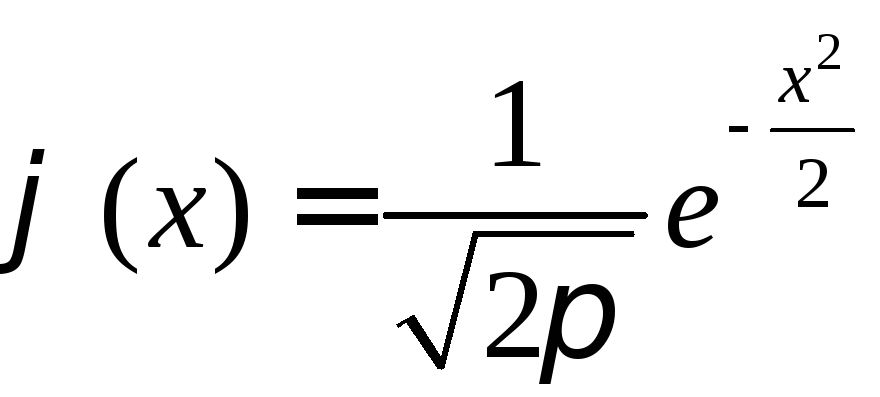 при
при .
(3.3)
.
(3.3)
Значения функции
![]() берутся из таблицы (прил.1),
при этом функция
берутся из таблицы (прил.1),
при этом функция
![]()
четная, т.е.
четная, т.е.
![]() .
.
Пример 3.5. Известно, что вероятность изготовления изделия первого сорта равна 0,8. Найти вероятность того, что в партии из 25 изготовленных изделий будет 21 изделие первого сорта.
Вероятность такого
события вычислим по локальной формуле
Лапласа (3.3) при
![]() и
и![]() .
Имеем
.
Имеем
![]() и
и
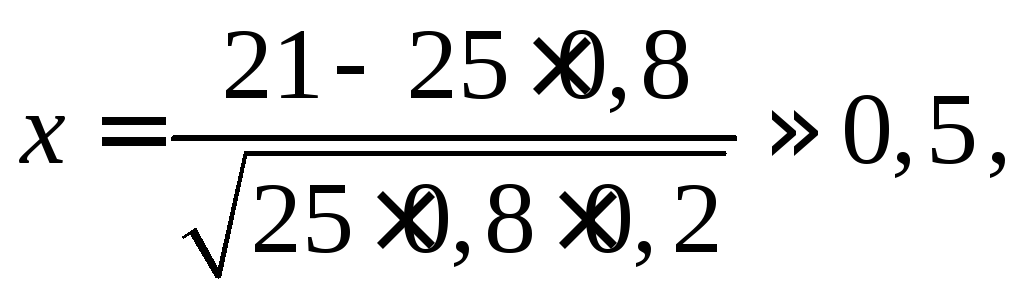
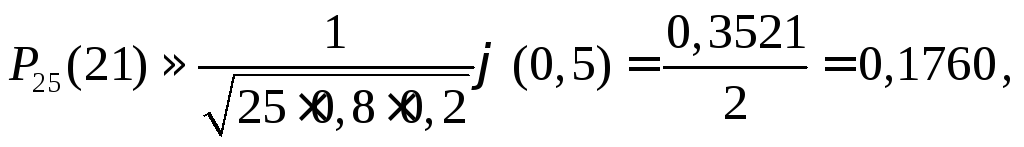
где значение
функции Лапласа
![]() взято из Приложения1.
взято из Приложения1.
Формула Бернулли (3.1) приводит нас к другому результату
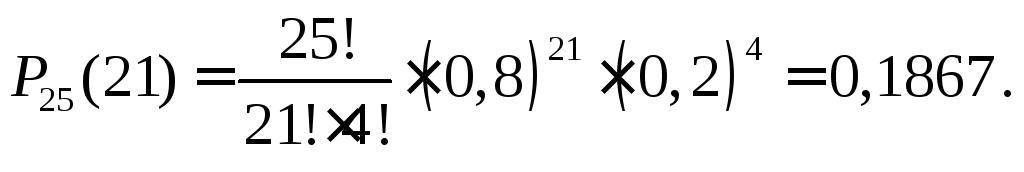
Отметим, что такое
довольно значительное отличие в
результатах объяс-няется очень просто
– формула Бернулли дает нам точный
результат, а формула Лапласа имеет
приближенный характер и дает хорошие
прибли-женные
результаты
только
при
достаточно
больших
значениях п
![]() .
.
Пример 3.6. Вероятность рождения мальчика равна 0,51. Найти веро-ятность того, что среди 100 новорожденных детей окажется ровно половина мальчиков.
Вероятность такого
события вычисляем по формуле (3.3) при
![]() и
и![]() .
Имеем
.
Имеем
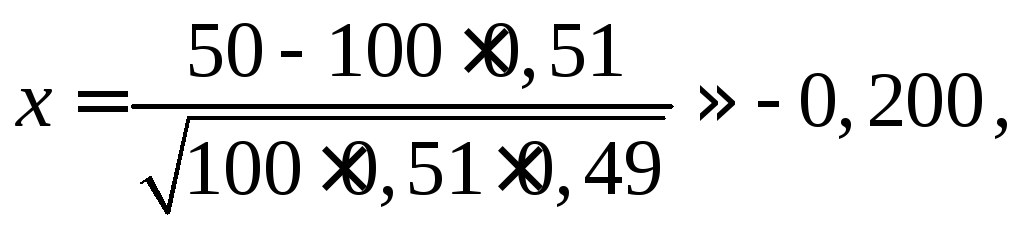
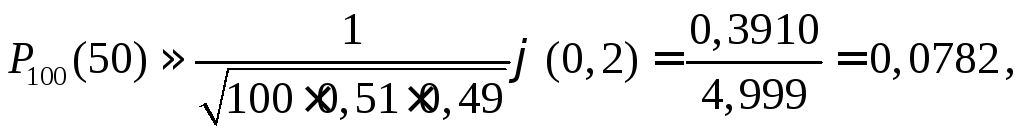
где значение
![]() взято из таблицы значений функции
взято из таблицы значений функции![]() .
.
Отметим, что в этом случае по формуле Бернулли (3.1) получаем уже достаточно близкий результат

3.3. Интегральная теорема Лапласа
Пусть производится
п
независимых испытаний. Как найти
вероятность
![]() того, что событиеА
появится в п
испытаниях не менее
того, что событиеА
появится в п
испытаниях не менее
![]() раз и не более
раз и не более![]() раз? Формулой
раз? Формулой![]() пользоваться не удобно. Ответ даёт
пользоваться не удобно. Ответ даёт
Теорема 3.2.
Если вероятность появления события А
в каждом из п
независимых испытаний постоянна и
равна р,
то вероятность
![]() при большихп
приближенно равна
при большихп
приближенно равна
 ,
,
где
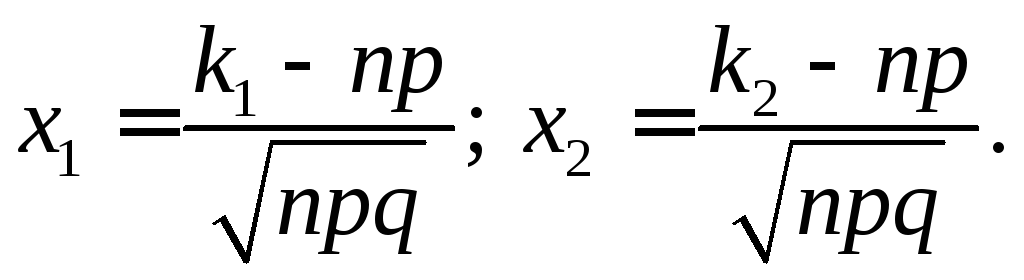
Для приближенного вычисления данного интеграла
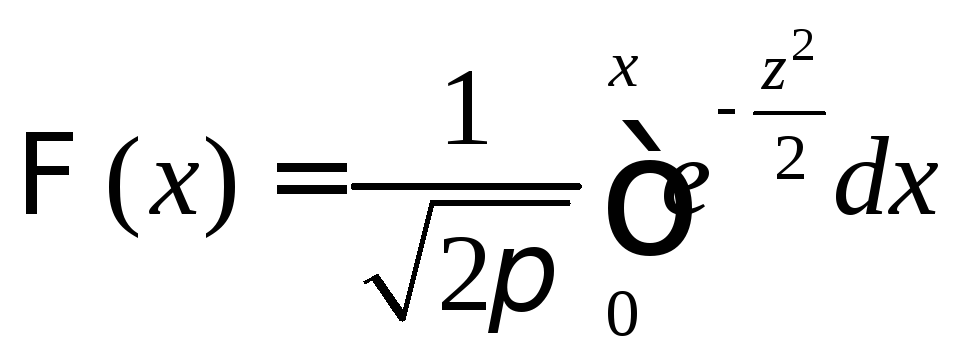 (функция Лапласа)
(функция Лапласа)
имеется таблица
(прил. 2),
при этом
функция
![]() нечетная, т.е.
нечетная, т.е.
![]() .
.
Тогда
![]() .
(3.4)
.
(3.4)
Замечание 3.2.
Погрешность вычислений вероятностей
по формулам (3.3) и (3.4) имеет порядок
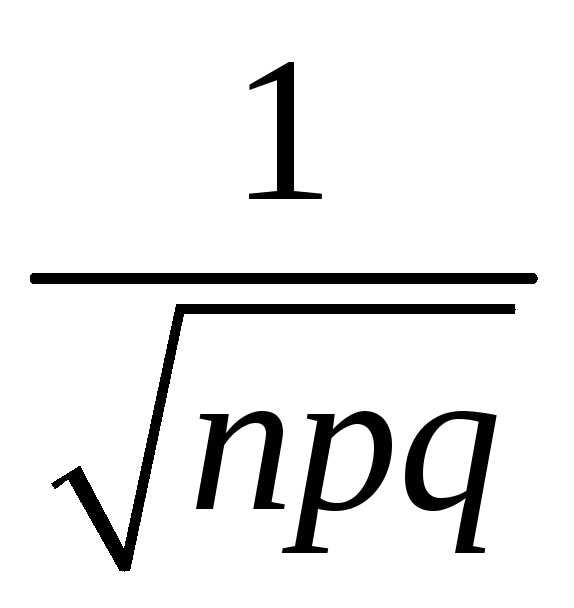 .
.
Пример 3.7. Вероятность того, что деталь прошла проверку ОТК, равна 0,2. Найти вероятность того, что среди 400 отобранных наудачу деталей окажется проверенных ОТК от 70 до 100.
По условию задачи
![]() и
и![]() .
.
Вычислим значения
![]() и
и![]()
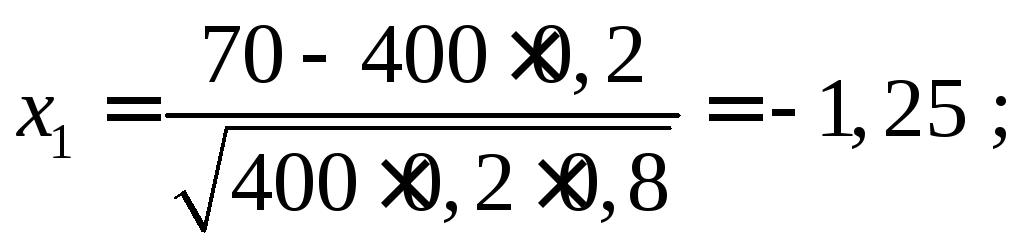

Тогда по интегральной формуле Лапласа (3.4) получим
![]()
![]()
Пример 3.8. Установлено, что в среднем каждое третье малое пред-приятие района имеет нарушения финансовой дисциплины. Найти веро-ятность того, что среди 200 зарегистрированных в районе малых пред-приятий имеют нарушения финансовой дисциплины: а) не более 60; б) не менее 80.
По условию
задачи вероятность того, что малое
предприятие имеет нарушения финансовой
дисциплины
![]() и
и![]() .
.
а) Необходимо
найти
![]()
Найдем
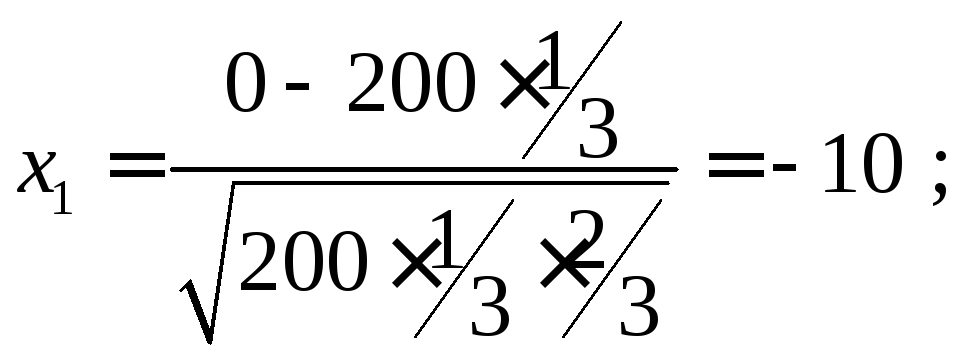
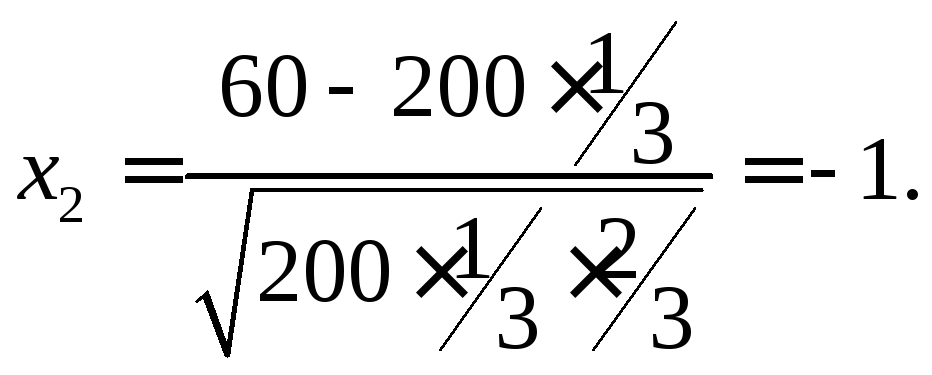
Тогда имеем
![]()
б) Необходимо
найти
![]()
Найдем
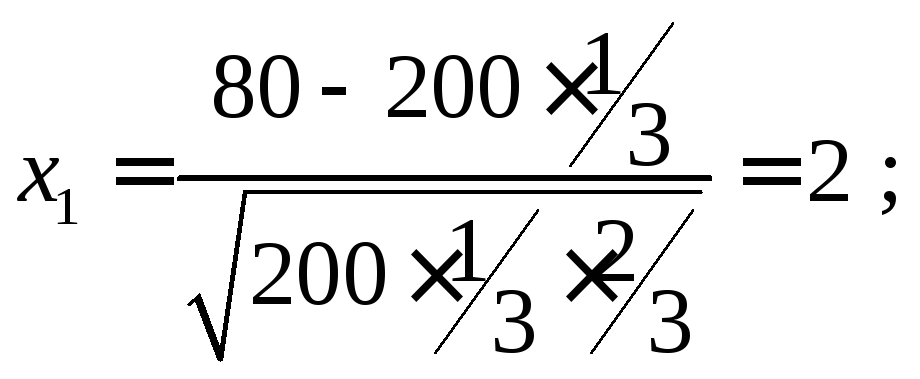
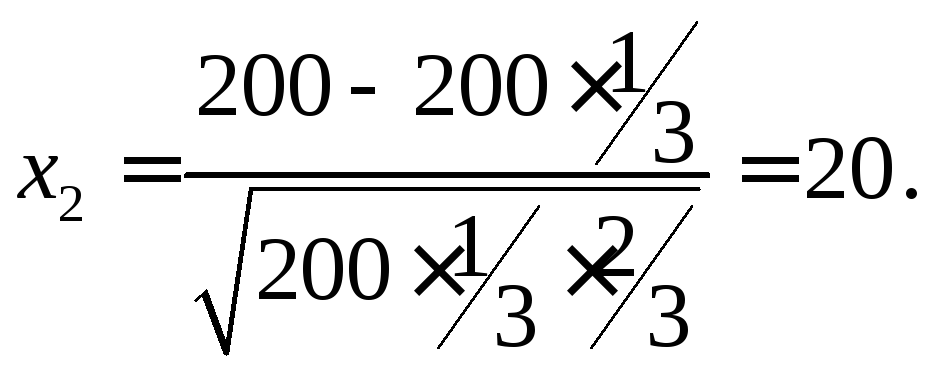
Тогда по интегральной формуле Лапласа (3.4) получим
![]()
