2.4. Формула Бейеса

Условия такие же, как и для формулы полной вероятности. Пусть событие А произошло, тогда вероятности гипотез могут быть переоценены по формуле Бейеса.

Теорема 2.4. 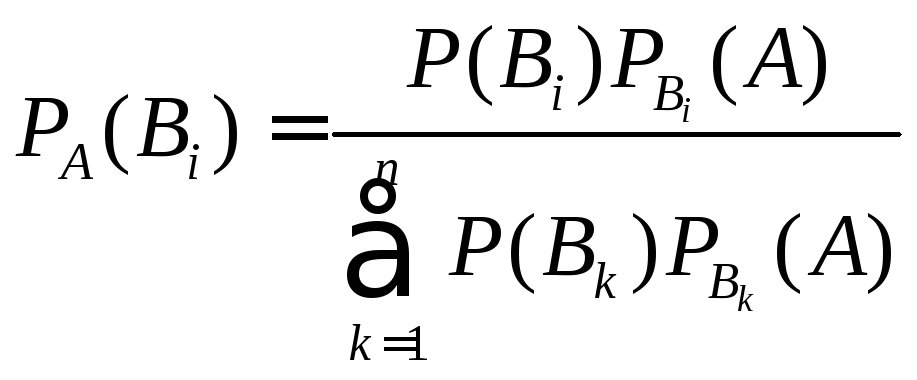. (2.6)

По теореме 2.1 умножения вероятностей имеем

или, с учетом формулы (2.5) полной вероятности, получаем

.

Пример 2.8. В магазин поступили телефоны от трех поставщиков в отношении4 : 5 : 1.Практика показывает,что телефоны,поступающие от 1-го, 2-го и 3-го поставщиков не потребуют ремонта в течении гарантийного срока в 88%, 98% и 92% случаев соответственно. Если проданный телефон потребовал ремонта в течение гарантийного срока, то от какого поставщика вероятнее всего поступил этот телефон?

В предыдущей задаче 2.7 мы нашли вероятность Р(В) = 0,91 того, что произвольно выбранный телефон не потребует ремонта в течение гарантийного срока. Поэтому вероятность того, что произвольно выбран-ный телефон потребует ремонта в течение гарантийного срока равна

По условию задачи условные вероятности того, что телефон потре-бует ремонта в зависимости от конкретного поставщика, равны:

Тогда по формуле Бейеса (2.6) получим

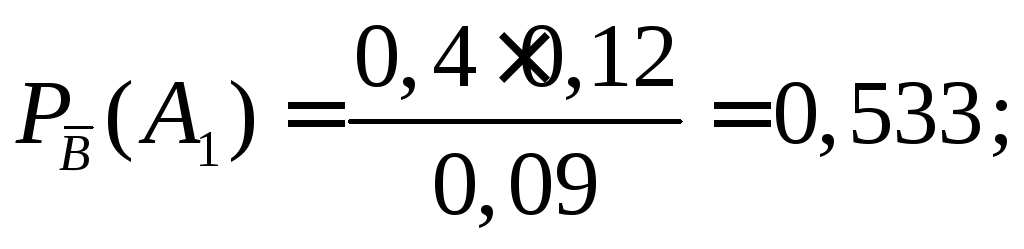
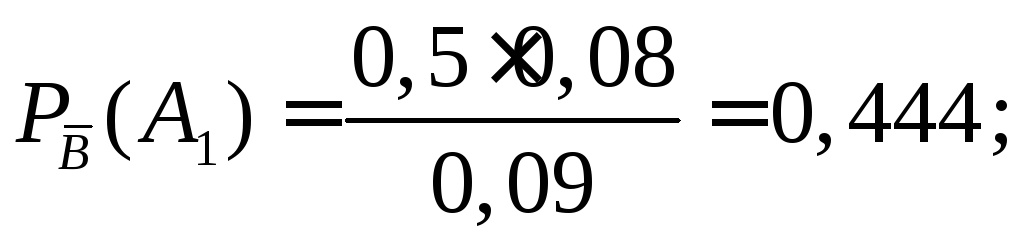
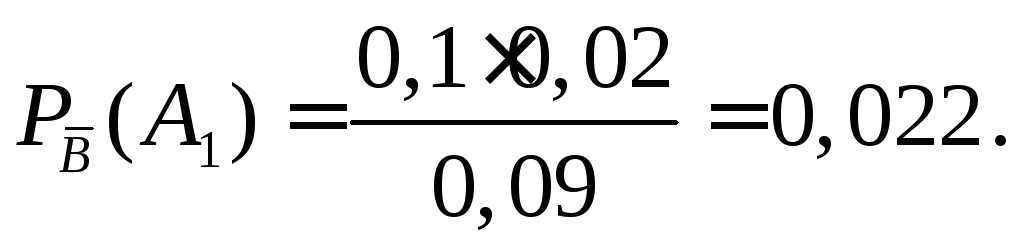
Таким образом, наиболее вероятным поставщиком неисправного теле-фона является первый поставщик.

Пример 2.9. Число грузовых автомашин, проезжающих по шоссе, на котором находится бензоколонка, относится к числу легковых как 3:2. Вероятность того, что будет заправляться грузовая автомашина, равна 0,1, легковая – 0,2. К заправке подъехала машина. Найти вероятность того, что эта автомашина грузовая.

Введём гипотезы:

- подъехала грузовая машина,

- подъехала легковая машина,

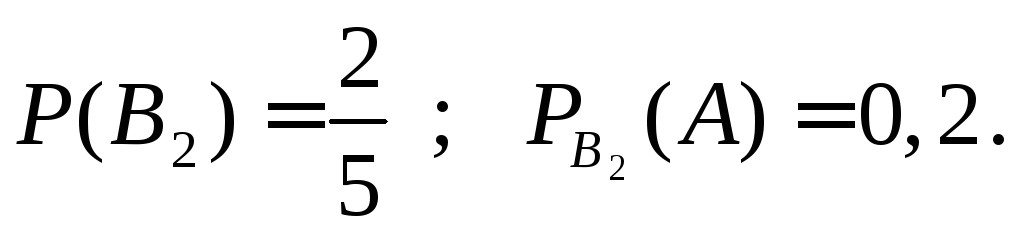
Тогда по формуле Бейеса (2.6) получим

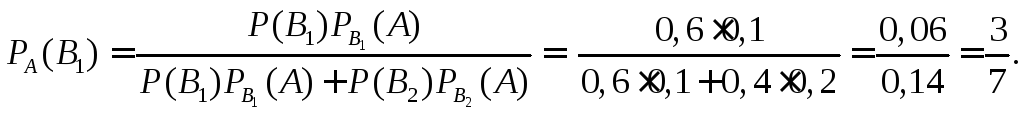
3. Повторение испытаний

3.1. Независимые испытания. Формула Бернулли

Испытание – это осуществление определённых условий, в результате которых может произойти то или иное элементарное событие простран-ства E. Если число исходов испытания - m, то назовём событие  i-м исходом . Обозначими будем считать, что все

события образуют полную группу событий, тогда

Пусть произведено n испытаний.

Определение 3.1. Если исходы испытания в каждом опыте не зависят от предыдущих исходов, то такие испытания называются независимыми.

Например, при бросании игральной кости, исходы: выпало одно, два очка и т.д. не зависят от предыдущих очков – испытания независимые.

Рассмотрим случай (схема Бернулли). Положим, т.е..

Рассмотрим следующую задачу. Пусть произведено n независимых испытаний, в каждом из которых событие A может появиться с одной и той же вероятностью р. Требуется найти  вероятность того, что событие А появится k раз, а событие появитсяраз.

Рассмотрим в какой-либо последовательности чередование событий А и так, чтобыА повторялось k раз, а событие появилосьраз. Это событие. По теореме умножения вероятностей получаем

.

По теореме сложения вероятностей равна сумме таких веро-ятностей для всех различных способов появлений событияА (k раз из п), т.е. их число . Поскольку все эти вероятности равны, то получаем формулу Бернулли

. (3.1)

Замечание 1. Так как все возможные исходы (событие А появилось 0 раз, 1 раз, 2 раза, … , п раз) образуют полную группу событий, то

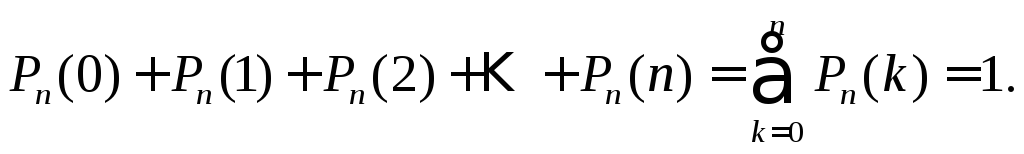
Пример 3.1. Вероятность изготовления стандартной детали токарем третьего разряда равна 0,7. Найти вероятности возможного количества бракованных деталей из 6, переданных потребителю.

Поскольку в задаче стоит вопрос о бракованных деталях, то именно вероятность изготовления бракованной детали обозначаем аПрименим формулу Бернулли (3.1):

Очевидно, что сумма всех найденных вероятностей равна 1.

Обратим внимание, что при вероятностьпринимает наи-большее значение, т.е. наиболее вероятно, что среди отобранных6 дета-лей окажется 2 бракованные. Для такого числа k будет справедливо неравенство

которое всегда имеет одно или два решения (если числа иявляются целыми).

Пример 3.2. Студент выучил 18 вопросов из 30, вынесенных на зачет. На зачете преподаватель предлагает ответить на три вопроса и в случае правильного ответа на два вопроса студент получает зачет. Найти веро-ятность сдачи зачета.

Очевидно, что вероятность правильного ответа студента на случайно выбранный вопрос равна а вероятность неправильного ответа

Для получения зачета студент должен ответить на два из трех или на все три вопроса, т.е. вероятность сдачи зачета

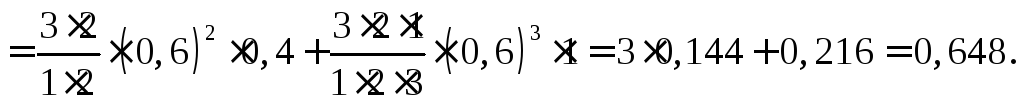
Пример 3.3. Вероятность хотя бы одного попадания при двух выстрелах равна 0, 96. Найти вероятность трёх попаданий при четырёх выстрелах.

Если  вероятность хотя бы одного попадания при двух выст-релах, то

,

тогда вероятность одного попадания и вероятность трёх попа-даний при четырёх выстрелах

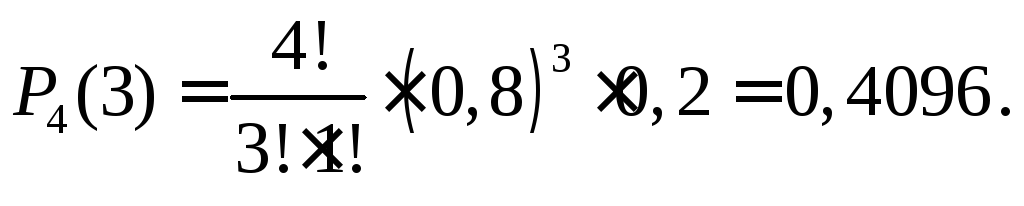
Рассмотрим более общий случай, когда при п испытаниях число исходов каждого испытания и пусть вероятность того, что событие произойдет.

Тогда вероятность того, что событие произойдетраз, событиепроизойдетраз,... и событие произойдетраз, вычис-ляется по формуле

(3.2)

где .

Пример 3.4. Игральная кость брошена 10 раз. Найти вероятность того, что одно очко выпадет два раза, два очка – ни разу, три очка – один раз, четыре очка – два раза, пять очков  три раза и шесть очков  два раза.

Здесь количество исходов испытаний

а вероятности этих исходов

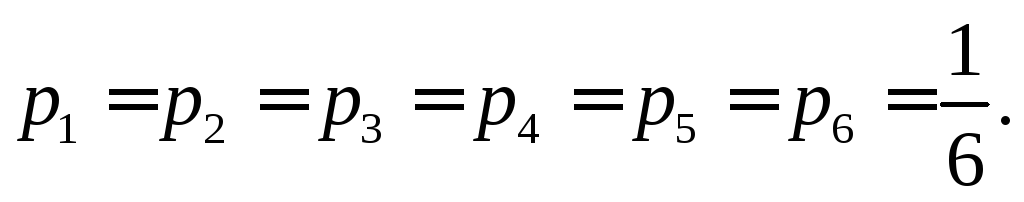
Тогда найдем искомую вероятность по формуле (3.2)