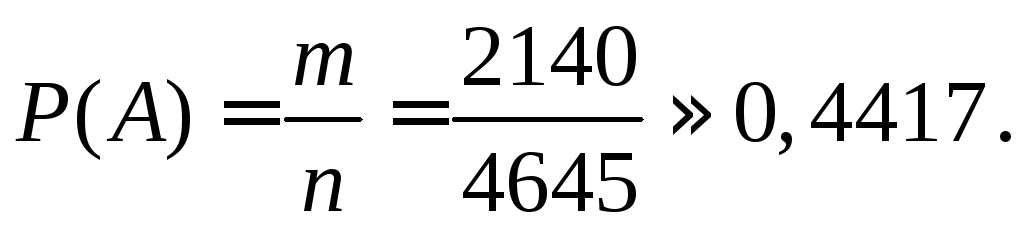- •Теория вероятностей и математическая статистика
- •Теория вероятностей
- •1. Общие понятия
- •1.1. Предмет теории вероятностей
- •1.2. Пространство элементарных событий
- •1.3. Операции над событиями
- •1.4. Статистический подход к понятию вероятности
- •1.5. Элементы комбинаторики
- •1. Перестановки.
- •2. Сочетания.
- •3. Размещения.
- •1.6. Классическое определение вероятности
- •1.7. Аксиоматическое определение вероятности
- •2. Основные теоремы теории вероятностей
- •2.1. Теорема умножения вероятностей
- •2.2. Теорема сложения вероятностей
- •2.3. Формула полной вероятности
- •2.4. Формула Бейеса
- •3. Повторение испытаний
- •3.1. Независимые испытания. Формула Бернулли
- •3.2. Локальная теорема Муавра – Лапласа
- •3.3. Интегральная теорема Лапласа
- •3.4. Теорема Пуассона
- •3.5. Вероятность отклонения частоты от постоянной вероятности в независимых испытаниях
- •4. Случайные величины и функции распределения
- •4.1. Случайные величины
- •4.2. Функция распределения вероятностей для дискретной св
- •4.3. Функция распределения вероятностей для непрерывной св.
- •4.4. Функция плотности распределения вероятностей
- •5. Числовые характеристики случайных величин
- •5.1. Математическое ожидание случайной величины
- •5.2. Дисперсия и среднее квадратическое отклонение св
- •5.3. Моменты и другие числовые характеристики случайной величины
- •6. Основные законы распределения случайных величин
- •6.1. Законы распределения дискретных случайных величин
- •6.1.1. Биномиальное распределение
- •6.1.2. Распределение Пуассона
- •6.1.3. Геометрическое распределение
- •6.2. Законы распределения непрерывных случайных величин
- •6.2.1. Равномерное распределение
- •6.2.2. Показательное распределение
- •6.2.3. Нормальное распределение
- •7. Закон больших чисел
- •7.1. Неравенства Чебышева
- •7.2. Теорема Чебышева
- •8. Многомерные случайные величины
- •8.1. Многомерные случайные величины и их функции распределения
- •X и y независимые случайные величины.
- •8.2. Вероятность попадания двумерной случайной величины
- •8.3. Числовые характеристики двумерной случайной величины
- •Математическая статистика
- •1. Статистические законы распределения выборки
- •1.1. Вариационный ряд
- •1.2. Полигон и гистограмма
- •1.3. Эмпирическая функция распределения
- •2. Статистические оценки параметров распределения
- •2.1. Точечные оценки
- •2.2. Интервальные оценки
- •2.3. Оценка вероятности появления события через его частоту
- •3. Проверка статистических гипотез.
- •3.1. Статистические гипотезы
- •3.2. Критерии проверки гипотезы
- •3.3. Критерий согласия Пирсона
- •3.4. Критерий согласия Романовского
- •4. Элементы теории корреляции
- •4.1. Статистические зависимости
- •4.2. Линейная регрессия
- •4.3. Корреляционная таблица
- •4.4. Выборочный коэффициент корреляции
- •Литература
- •С о д е р ж а н и е
3. Размещения.
Всякое упорядоченное подмножество, содержащее k элементов данного множестваМ из n элементов, называется размещением из n элементов по k.
Число размещений
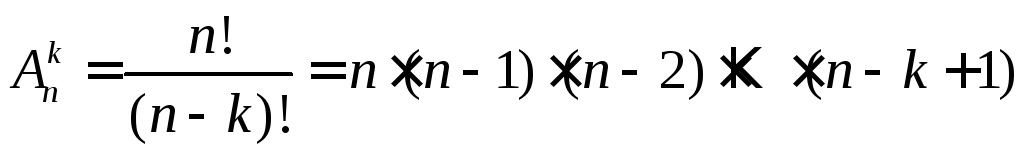 .
.
Пример 1.15. Сколько различных трехзначных чисел можно соста-вить из цифр 1, 2, 3, 4 и 5 ?
Поформуледляразмещений находим количество всевозможных трех-
значных чисел
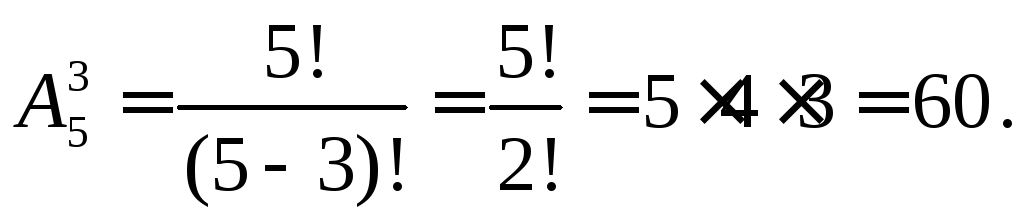
Замечание. Часто при решении задач число п достаточно велико, поэтому в таких случаях полезно использовать формулу Стирлинга
![]()
4. Основные правила комбинаторики.
Правило суммы.
Если некоторый объект
![]() можно выбратьп
разными способами,а
объект
можно выбратьп
разными способами,а
объект
![]() можно выбратьт
разными способами, причем никакой
выбор
можно выбратьт
разными способами, причем никакой
выбор
![]() не совпадает ни с каким выбором
не совпадает ни с каким выбором![]() ,
то один из объектов
,
то один из объектов![]() или
или![]() можно выбрать
можно выбрать![]() способами.
способами.
Пример 1.16. На двух полках находится 35 и 40 книг соответственно. Сколькими способами можно выбрать одну книгу ?
По правилу суммы
находим число всех возможных способов
выбора
![]()
Правило
произведения.
Если некоторый объект
![]() можно выбратьп
разными способами и при каждом выборе
объекта
можно выбратьп
разными способами и при каждом выборе
объекта
![]() объект
объект![]() можно выбратьт
разными способами, то выбор пары объектов
можно выбратьт
разными способами, то выбор пары объектов
![]() можно осуществить
можно осуществить![]() способами.
способами.
Пример 1.17. В группе 20 студентов, из них 8 юношей и 12 девушек. Сколькими способами можно выбрать одного юношу и одну девушку для участия в конкурсе?
Каждый из п
= 8
вариантов выбора юноши может комбинироваться
с одним из т
= 12
вариантов выбора девушки, поэтому по
правилу произведения число способов
выбора пары равно
![]()
Пример 1.18. В группе 20 студентов, из них 8 юношей и 12 девушек. Сколькими способами можно выбрать двух юношей и трех девушек для участия в конкурсе?
Каждый из
![]() вариантов выбора двух юношей может
комбинироваться с одним из
вариантов выбора двух юношей может
комбинироваться с одним из![]() вариантов выбора девушки,
поэтому по
правилу произведения
вариантов выбора девушки,
поэтому по
правилу произведения
число способов выбора равно
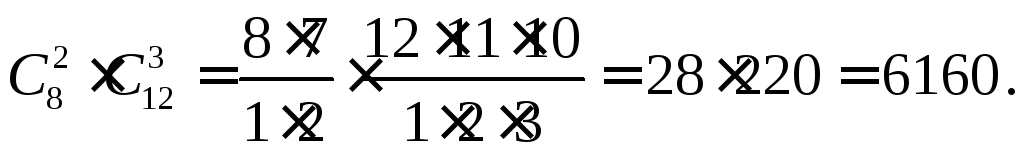
1.6. Классическое определение вероятности
Это определение относится только к тем опытам, у которых возможно конечное число равновозможных исходов. Исходы являются равновозмож-ными, если нет оснований считать, что ни один из них будет более воз-можным, чем другие. Например, если брошена игральная кость, то исходы: выпало одно очко, - два очка, …, - шесть очков – являются равно-возможными.
Определение
1.12. Вероятностью
события А
называется число
 ,
гдеn
число всех исходов опыта, а т
число исходов, благоприятных появлению
события А.
,
гдеn
число всех исходов опыта, а т
число исходов, благоприятных появлению
события А.
Из определения следуют основные свойства вероятности:
1.
![]() ,
так как
,
так как![]() ;
;
2.
![]() ,
так как в этом случае
,
так как в этом случае![]() ;
;
3.
![]() ,
так как в этом случае
,
так как в этом случае![]() .
.
Пример 1.19. Брошены две игральные кости. Найти вероятность того, что выпадет в сумме три очка.
Пусть А
интересующее нас событие. Благоприятные
исходы: (1
, 2)
и (2,
1),
т.е.
![]() .
Число общих исходов определяем из того,
что каждое число
очков на
одной кости
может сочетаться с шестью вариантами
числа
.
Число общих исходов определяем из того,
что каждое число
очков на
одной кости
может сочетаться с шестью вариантами
числа
очков на другой
кости, т.е.
![]() .
Тогда
.
Тогда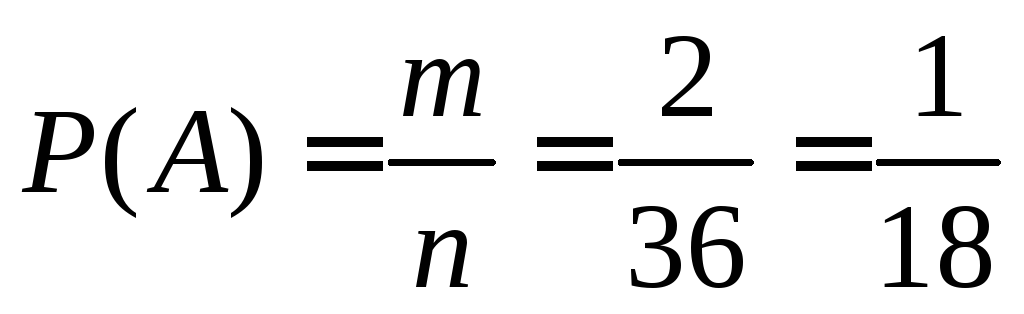 .
.
Пример 1.20. Абонент забыл последние три цифры семизначного номера телефона и, помня, что они различные, набрал их наугад. Найти вероятность того, что он набрал правильный номер.
Пусть А
- интересующее нас событие. Очевидно,
что
![]() .
Число различных вариантов набора трёх
различных цифр
из
десяти будет
равно
.
Число различных вариантов набора трёх
различных цифр
из
десяти будет
равно
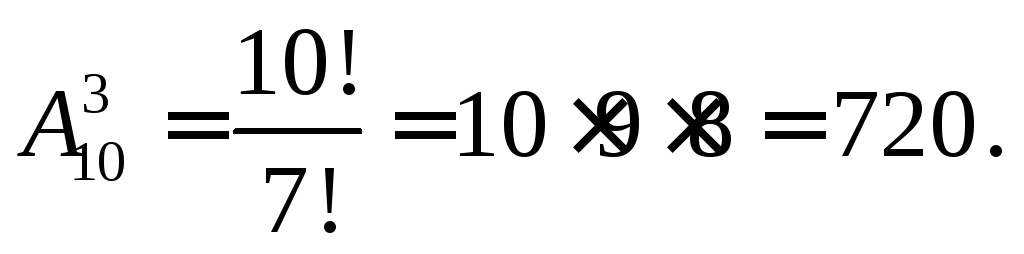 Тогда
Тогда
 .
.
Пример 1.21.
Некий гражданин купил карточку лото и
наугад отметил 6
номеров из 49.
Найти вероятность того, что он правильно
угадал k
номеров из 6
![]() .
.
Пусть А
интересующее нас событие. Общее число
исходов
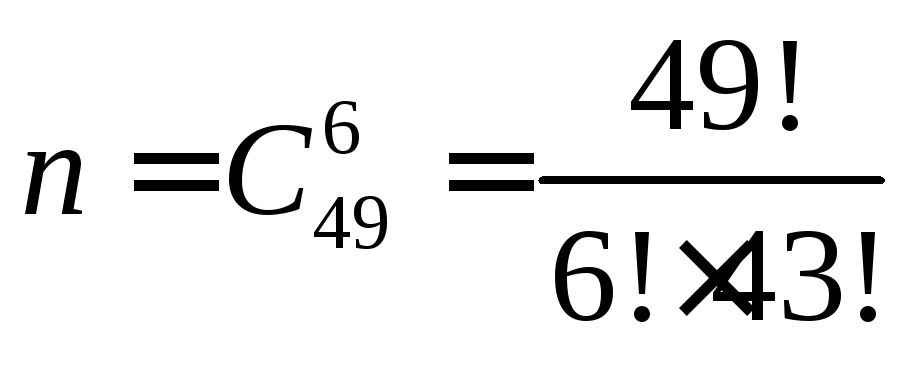 .
Число угаданных
.
Число угаданных
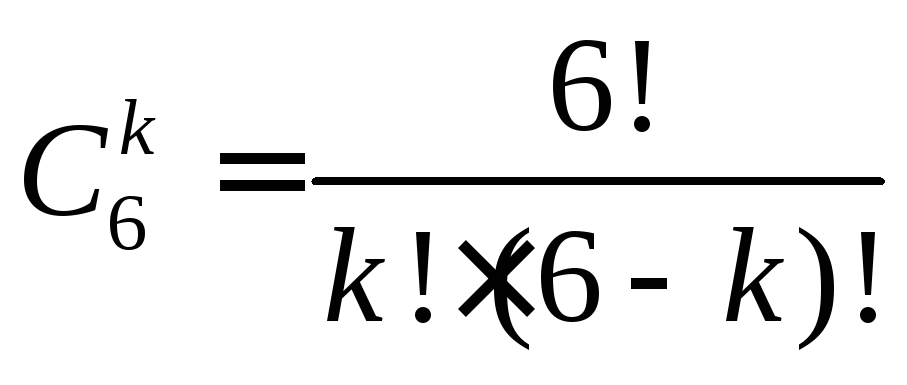 ,
каждый из этих вариантов может сочетаться
с одним из
,
каждый из этих вариантов может сочетаться
с одним из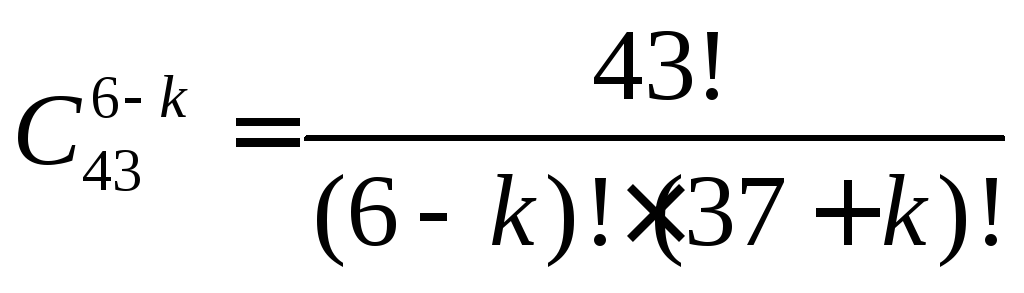 непра-вильных вариантов.
непра-вильных вариантов.
Тогда
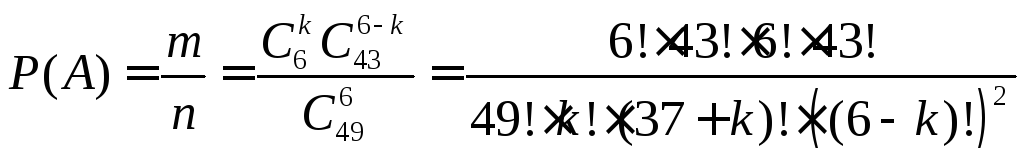 .
.
откуда следует,
что вероятность минимального выигрыша
в лото при
![]() будет равна
будет равна![]() .
.
Пример 1.22. Магазин продал 16 из 20 кухонных комбайнов трех марок, имеющихся в продаже в количестве 4, 7 и 9 штук соответственно. Полагая, что вероятность быть проданным для каждого комбайна одинакова, найти вероятности того, что остались непроданными кухонные комбайны: а) только одной марки; б) всех трех марок.
а) Если осталось
непроданных 4
кухонных комбайна из 20
(событие А),
то число вариантов, при которых это
событие может произойти равно
![]()
Число вариантов,
при которых останутся непроданными
все 4
кухонных комбайна первой марки, равно
![]() число вариантов, при которых останутся
непроданными4
комбайна второй марки, равно
число вариантов, при которых останутся
непроданными4
комбайна второй марки, равно
![]() и, наконец,
число вариантов,
при которых останутся непроданными 4
комбайна третьей марки, равно
и, наконец,
число вариантов,
при которых останутся непроданными 4
комбайна третьей марки, равно
![]()
Тогда для события А по правилу суммы общее число вариантов
![]()
и искомая вероятность равна
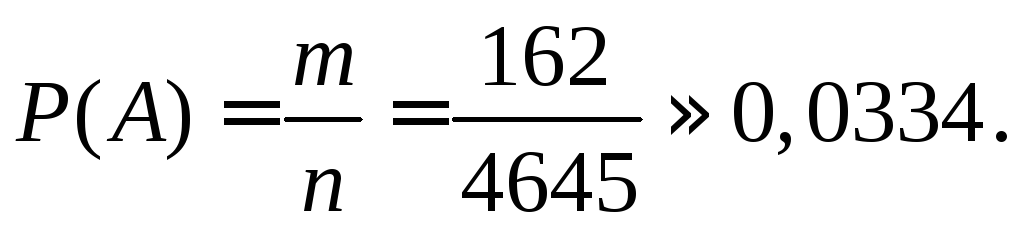
б) В случае, если останутся непроданными кухонные комбайны всех трех марок (событие В), то это может произойти тремя способами: ку-хонных комбайнов одной из марок останется 2, а комбайнов остальных двух марок по одному.
Таким образом, если останется 2 комбайна первой марки, то по правилу произведения количество интересующих нас вариантов равно
![]()
если останется 2 комбайна второй марки, то по правилу произведения количество интересующих нас вариантов равно
![]()
и, наконец, если останется 2 комбайна третьей марки, то по правилу произведения количество интересующих нас вариантов равно
![]()
Общее количество вариантов, при которых произойдет событие В,
![]()
и искомая вероятность равна