2.3. Оценка вероятности появления события через его частоту

Пусть осуществлена серия из п последовательных независимых испы-таний и в k случаях произошло событие А. Считая, что вероятность р появления события А одинакова в каждом испытании, оценим искомую вероятность.

Применим к задаче оценки вероятности наблюдаемого события следствиеиз интегральной теоремы Лапласа:

(2.3)

Если нам задан уровень надежности , то по таблице (Прил. 5) най-дем tиз условия. Тогда соотношение (2.3) можно записать

где величина  определяется из условия

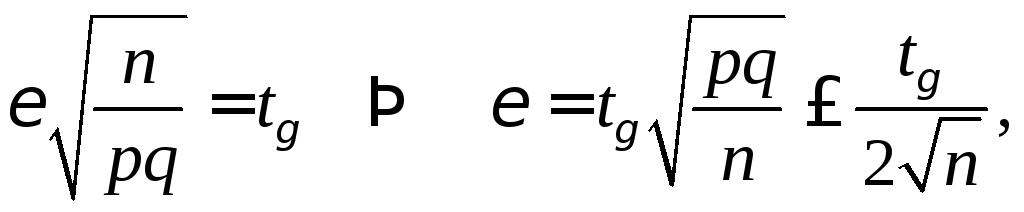(2.4)

так как (см. п.7.2). В итоге соотношение (2.3) примет вид

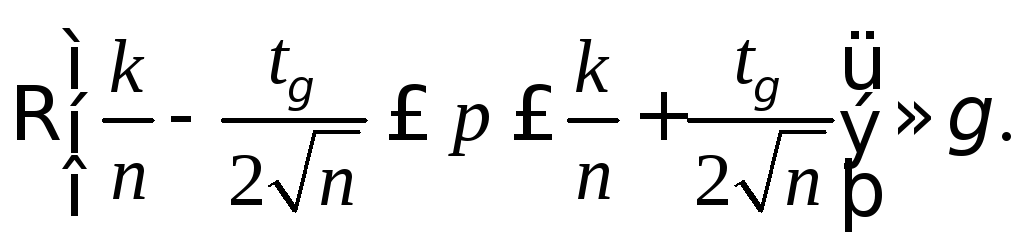
Замечание. Если вероятность p из неравенства (2.4) оценить реальной

частотой наблюдаемого события, а не, то величина уменьшится, а, следовательно, сузится и доверительный интервал.

Пример 2.3. Монету подбросили 900 раз и при этом герб выпал 540 раз. Полагая уровень надежности , выяснить, согласуется ли этот результат с предположением о том, что монета изготовлена из однородного материала и имеет стандартные размеры.

Из таблицы (Прил. 5) находим t = 3,291, поэтому

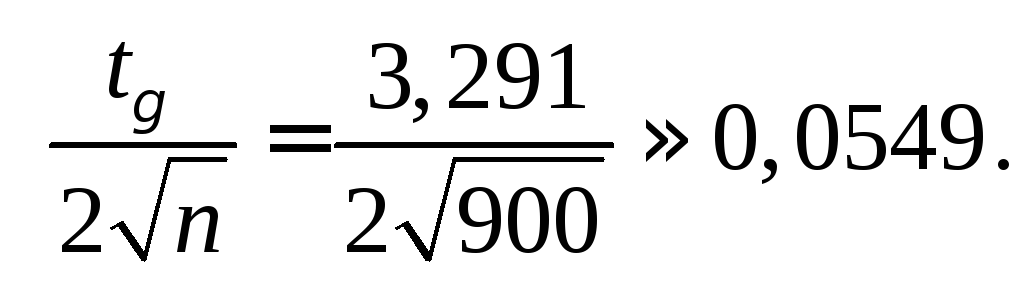
Если бы наше предположение было верным, то с вероятностью 0,999

разность должна быть не больше чем0,0549. Но по данным

опытов герб выпал 540 раз из 900 бросаний, а, поскольку вероятность выпадения герба то имеем

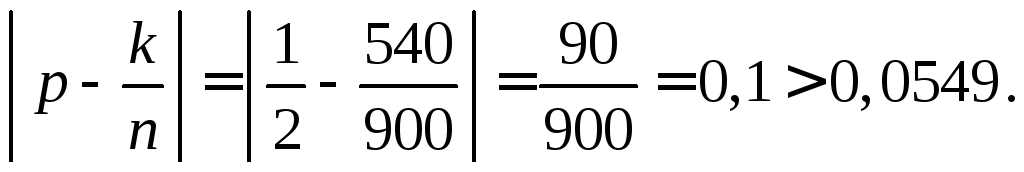
Таким образом, с вероятностью 0,999 можно утверждать, что исполь-зуемая при бросании монета не является стандартной.

Учитывая статистический смысл понятия вероятности, полученному результату можно дать такое объяснение: если осуществлять много серий бросаний монеты (по 900 раз в каждой серии), то в среднем не более чем в 0,1% серий (1 серия из 1000) может выполняться неравенство

или

Поэтому, можно считать практически невозможным, что в одной из серий из 900 бросаний монеты герб выпадет больше чем 500 раз.

Пример 2.4. В пруд выпустили 100 меченых рыб (n). Незадолго пос-ле этого было выловлено 400 рыб, среди которых было выявлено ровно 5 меченых (k). Оценить общее количество рыб N в пруду с заданной надеж-ностью .

Оценим вероятность вылова меченой рыбы по частоте .

Находим t=1,96 из таблицы (прил.5) и по формуле (2.4) с учетом приведенного выше замечания имеем

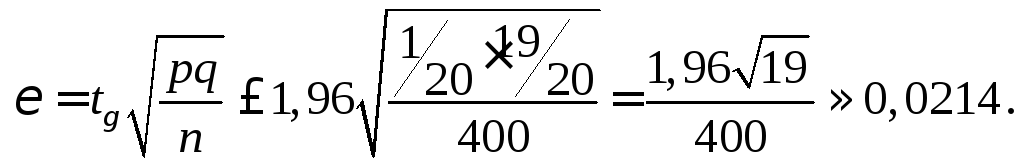
Таким образом, для общего количества рыб в пруду с заданной вероятностью должно выполняться неравенство

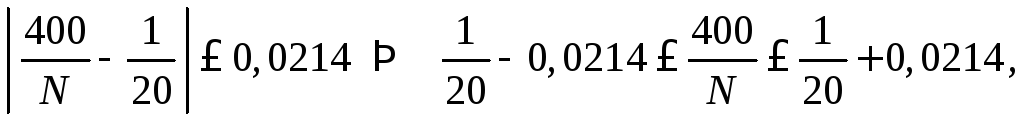
Отсюда получаем искомую оценку общего количества рыб в пруду

3. Проверка статистических гипотез.

3.1. Статистические гипотезы

Часто в задачах практики на основании тех или иных данных делается предположение (гипотеза) о виде закона распределения интересующей нас случайной величины или о параметрах известных распределений. Однако для окончательного решения вопроса о виде закона распределения или предполагаемой величине исследуемого параметра нужно проверить насколько сделанные предположения (гипотезы) согласуются с имеющимися опытными данными. Поскольку такую проверку осуществляют статисти-ческими методами, то выдвинутую гипотезу принято также называть статистической. Здесь мы будем рассматривать только гипотезы о виде закона распределения случайной величины.

Вместе с выдвинутой гипотезой рассматривают и противоречащую ей гипотезу. Выдвинутую гипотезу обычно называют нулевой или основной и обозначают , а гипотезу , противоречащую нулевой, называют альтернативной или конкурирующей.

Выдвинутая гипотеза может быть как верной, так и неверной, поэтому при ее проверке может быть принято как верное, так и неверное решение. Если будет отвергнута верная гипотеза, то это ошибка первого рода, а если будет принята неверная гипотеза  это ошибка второго рода.

Вероятность совершить ошибку первого рода называют уровнем значимости и обычно обозначают через . Наиболее часто уровень значимости принимают равным 0,05 или 0,01. Это означает, что если, например, уровень значимости принят равным = 0,01, то вероятность совершить ошибку первого рода равна 0,01.

Отметим, что правильное решение может быть принято в двух случаях:

 гипотеза принимается и в действительности она верна;

 гипотеза отвергается и в действительности она неверна.

Если нулевая гипотеза принята, то это еще не означает, что она верна. Один единственный рассмотренный пример, подтверждающий нашу гипотезу, ее верность не доказывает. В данном случае, следует считать, что данные выборки согласуются с нулевой гипотезой и, следовательно, нет никаких оснований ее отвергнуть. Другими словами, верность гипотезы следует подтвердить другими способами, например, увеличив объем выборки. А вот для отклонения нулевой гипотезы достаточно привести единственный пример, который ей противоречит.