6.2.3. Нормальное распределение

Определение 6.5. Случайная величина X называется распределённой по нормальному закону, если функция плотности распределения имеет

вид .

Определим смысл параметров a и . Для этого вычислим:

,

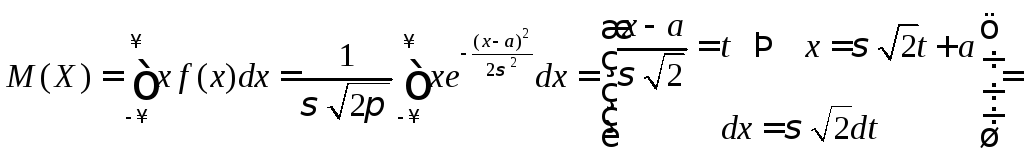
так как первый интеграл равен нулю, как интеграл от нечетной функции в симметричных пределах, а второй (интеграл Пуассона) равен

Таким образом, . Аналогично можно показать, что, т.е..

График функции нормального распределения имеет вид

f(х)

О а х

Здесь точкаmax, точки перегиба, .

Если вычислить значения центральных моментов

,

то получим

Тогда для нормального распределения коэффициент асимметрии  As и эксцесс  Ex будут равны:

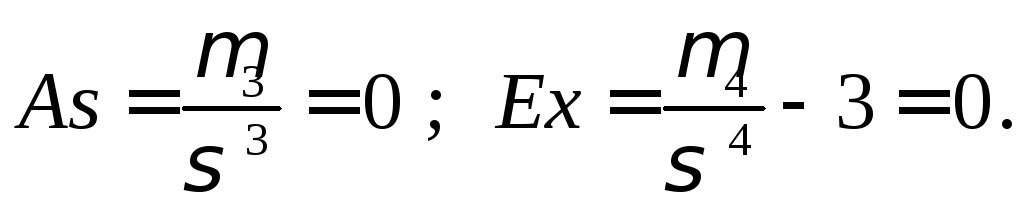
Таким образом, эти коэффициенты определяют степень отклонения распределения от нормального.

Вероятность попадания в заданный интервал случайной величины, имеющей нормальное распределение, определяется по формуле

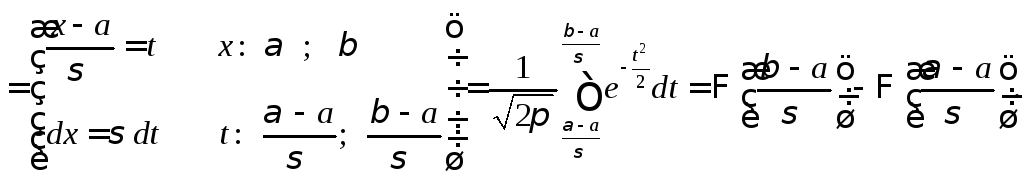(6.1)

Следствие 1. При ииз формулы (6.1) получаем

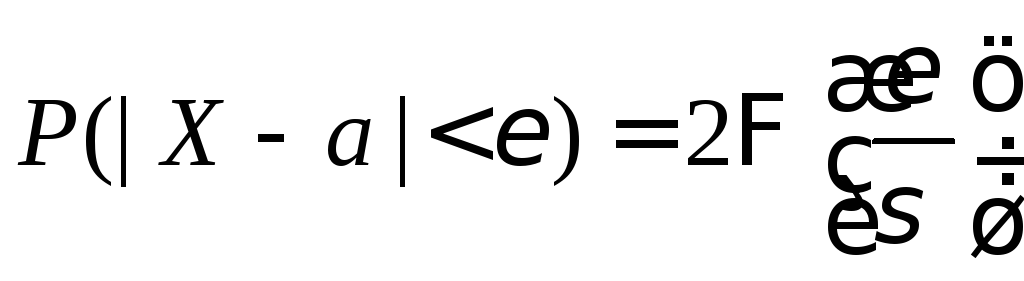. (6.2)

Следствие 2. Если положить в формуле (6.2) и учесть, что при, то получим

. (6.3)

Выражение (6.3) представляет собой так называемое правило трёх сигм. Оно означает, что практически в интервале находятся все возможные значения нормально распределённой случайной величины.

Нормальный закон распределения играет в теории вероятностей важную роль, так как является предельным законом, к которому приближаются многие другие законы. Это отражено в центральной предельной теореме Ляпунова.

Теорема. Если Х  сумма большого числа независимых случайных величин , которые имеют различные распределения и их влияние на случайную величинуХ незначительно, то Х имеет распределение близкое к нормальному. А в пределе распределение случайной величины Х стремится к нормальному закону.

Нормальный закон широко используется в теории ошибок, в теории стрельбы, теории надёжности и т.д.

Пример 6.8. По цели, имеющей вид полосы, ширина которой 20 м, ведётся стрельба в направлении перпендикулярном полосе. Прицеливание ведётся по средней линии. Среднее квадратическое отклонение (точность прицела) в направлении стрельбы равна . Найти вероятность попадания в цель при одном выстреле.

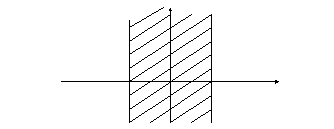
у

10 а = 0 10 х

Здесь

Полагая в формуле (6.2) эти значения, получаем

7. Закон больших чисел

Этот закон обосновывает устойчивость средних, т.е. при очень большом числе случайных событий их средний результат практически перестаёт быть случайным и может быть предсказан с большой точностью. Какие условия необходимы для этого?

7.1. Неравенства Чебышева

Теорема 7.1. Если случайная величина Х имеет конечную дисперсию, то справедливо неравенство

.

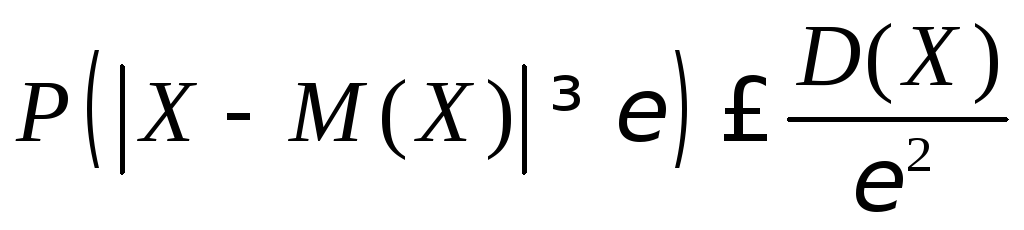Доказательство проведём для непрерывной случайной величины.

Из рисунка

х

следует

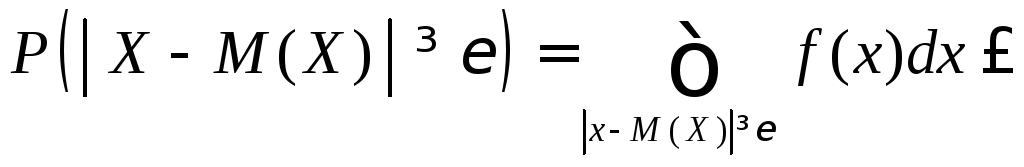
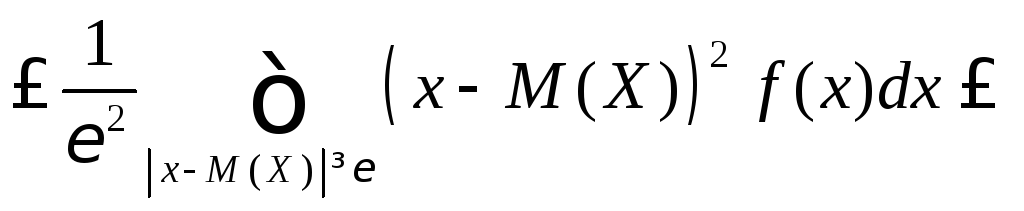
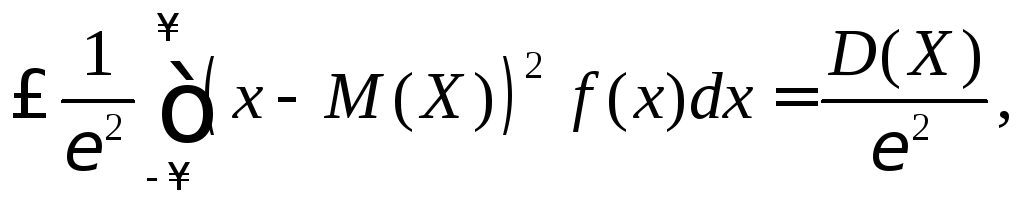
что и требовалось доказать.

Пример 7.1. Дана случайная величина Х с математическим ожиданием и дисперсией. Оценить вероятность того, что случайная величина Х отклонится от своего математического ожидания не менее, чем на .

Положим в неравенстве Чебышева , тогда

,

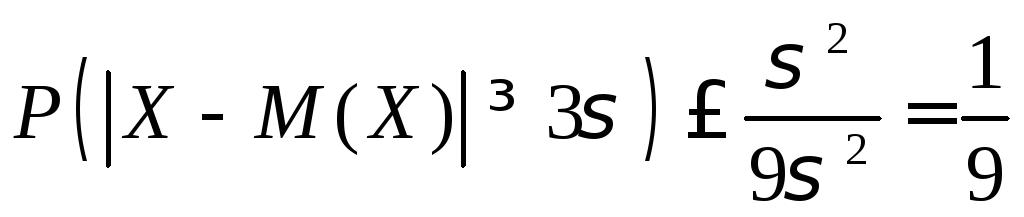что верно для всех законов распределения случайной величины.

Теорема 7.2. Если случайная величина Х принимает только неотрица-тельные значения и имеет конечное математическое ожидание, то для лю-бого числа выполняется неравенство

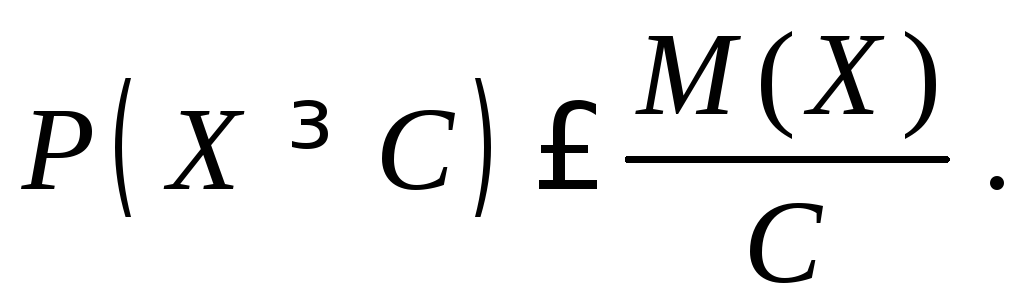
Доказательство проведём для дискретной СВ. Имеем

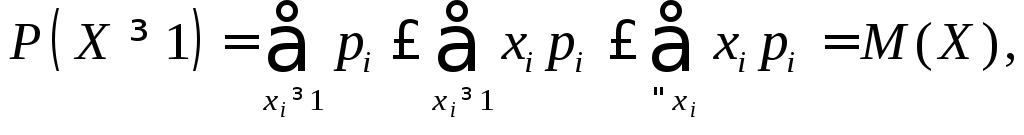
откуда, воспользовавшись свойством математического ожидания, получим

Это другая форма неравенства Чебышева.

Пример 2. Среднее число некондиционных устройств в одной партии равно 4. Оценить вероятность того, что в следующей партии устройств будет не больше 12 некондиционных.

Подставив в неравенстве Чебышева и, получим

и