5.2. Дисперсия и среднее квадратическое отклонение св

Математическое ожидание полностью не характеризует случайную ве-личину. Поэтому вводят другие числовые характеристики.

Определение 5.2. Отклонением или центрированной случайной вели-чиной называется разность .

Легко показать, что .

Определение 5.3. Дисперсией случайной величины называется матема-тическое ожидание квадрата отклонения случайной величины Х от своего математического ожидания и обозначается

.

Из этого определения следует, что дисперсия характеризует меру рассеивания возможных значений около её математического ожидания.

Определение 5.4. Величина называетсясредним квадра-тическим отклонением.

Получим более удобную формулу для вычисления дисперсии.

.(5.3)

Тогда для дискретной случайной величины формула для вычисления дисперсии примет вид

или . (5.4)

Для непрерывной случайной величины 

или . (5.5)

Свойства дисперсии:

1. , как сумма неотрицательных членов, или как интеграл от неотрицательной функции.

2. , так как.

3. , что следует непосредственно из определения дисперсии.

4. Если Х и Y независимые СВ, то .

Действительно,

(с учетом свойств математического ожидания)

Пример 5.3. Найти математическое ожидание , дисперсиюи среднее квадратическое отклонениеслучайной величины с плот-ностью распределения

По формулам (5.2), (5.4) и (5.5) соответственно находим:

.

5.3. Моменты и другие числовые характеристики случайной величины

Кроме математического ожидания и дисперсииприме-няются и другие числовые характеристики случайной величины.

Определение 5.5. Начальным моментом k-го порядка случайной вели-чины Х называется значение .

Тогда для дискретных случайных величин: .

Для непрерывных случайных величин: .

Определение 5.6. Центральным моментом k-го порядка случайной вели-чины Х называется значение .

Тогда для дискретных случайных величин: .

Для непрерывных случайных величин: .

Легко проверить следующие соотношения:

и установить связь между начальными и центральными моментами:

.

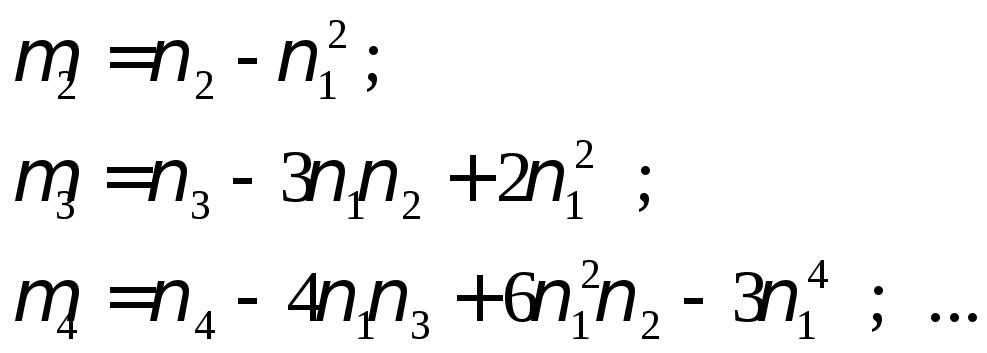Моменты характеризуют то или иное свойство случайных величин. Например, момент (дисперсия) характеризует рассеивание значений случайной величины около математического ожидания, момент асимметрию и т.д. Моменты более высокого порядка практически не используются.

Замечание. Рассмотренные здесь моменты принято называть теоретичес-кими в отличие от моментов, которые определяются по данным наблюде-ний. Их называют эмпирическими.

Рассмотрим еще несколько числовых характеристик случайной вели-чины, которые также используются в теории вероятностей и математи-ческой статистике.

Определение 5.7. Медианой распределения случайной величиныХ называется такое значение аргумента х = т, для которого выполняется

равенство

Например, для непрерывных СВ такое значение всегда существует, так как функция распределения монотонно возрастает от0 до 1. Действительно, так как функция распределениянепрерывна, то такое значение существует по теореме о промежуточных значениях непрерывной функции. А если график функции распределения имеет с прямой

общий отрезок, то любую точку этого отрезка можно считать медианой распределения.

Определение 5.8. Квантилем распределения случайной величины Х по-рядка корень уравнения.

Таким образом, медиана т распреде-

ления – это квантиль порядка . Если 1

у некоторого распределения известны

квантили для нескольких значений р, то

они могут дать достаточно полное пред-

ставление о характере рассматриваемого

распределения. т х

На практике обычно пользуются квантилями для р = 0,1 ; 0,2 ; …; 0,9

(их называют децилями) и для р = ; (их называютквартилями).

Определение 5.9. Модой распределения непрерывной случайной вели-чины Х называется каждое значение х случайной величины, при котором функция плотности распределения имеет максимум.

Большинство распределений обычно

имеют единственную моду – такие распре-1

деления называют унимодальными.

Например, распределение непрерывной

случайной величины, имеющее функцию0 1 2 х

плотности , график которой изображен на рисунке является унимо-дальным с модойх = 1.

Определение 5.10. Случайную величину Х называют симметричной относительно точки а, если .

Тогда для функции распределения непрерывной симметричной СВ будет справедливо равенство . Для симметричной слу-чайной величины центральные моменты нечетного порядка будут равны0, в связи с чем вводится коэффициент асимметрии (безразмерная величина)

.