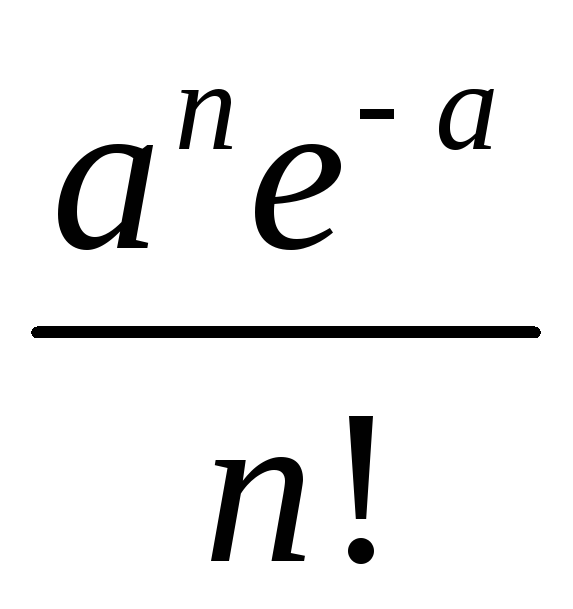- •Теория вероятностей и математическая статистика
- •Теория вероятностей
- •1. Общие понятия
- •1.1. Предмет теории вероятностей
- •1.2. Пространство элементарных событий
- •1.3. Операции над событиями
- •1.4. Статистический подход к понятию вероятности
- •1.5. Элементы комбинаторики
- •1. Перестановки.
- •2. Сочетания.
- •3. Размещения.
- •1.6. Классическое определение вероятности
- •1.7. Аксиоматическое определение вероятности
- •2. Основные теоремы теории вероятностей
- •2.1. Теорема умножения вероятностей
- •2.2. Теорема сложения вероятностей
- •2.3. Формула полной вероятности
- •2.4. Формула Бейеса
- •3. Повторение испытаний
- •3.1. Независимые испытания. Формула Бернулли
- •3.2. Локальная теорема Муавра – Лапласа
- •3.3. Интегральная теорема Лапласа
- •3.4. Теорема Пуассона
- •3.5. Вероятность отклонения частоты от постоянной вероятности в независимых испытаниях
- •4. Случайные величины и функции распределения
- •4.1. Случайные величины
- •4.2. Функция распределения вероятностей для дискретной св
- •4.3. Функция распределения вероятностей для непрерывной св.
- •4.4. Функция плотности распределения вероятностей
- •5. Числовые характеристики случайных величин
- •5.1. Математическое ожидание случайной величины
- •5.2. Дисперсия и среднее квадратическое отклонение св
- •5.3. Моменты и другие числовые характеристики случайной величины
- •6. Основные законы распределения случайных величин
- •6.1. Законы распределения дискретных случайных величин
- •6.1.1. Биномиальное распределение
- •6.1.2. Распределение Пуассона
- •6.1.3. Геометрическое распределение
- •6.2. Законы распределения непрерывных случайных величин
- •6.2.1. Равномерное распределение
- •6.2.2. Показательное распределение
- •6.2.3. Нормальное распределение
- •7. Закон больших чисел
- •7.1. Неравенства Чебышева
- •7.2. Теорема Чебышева
- •8. Многомерные случайные величины
- •8.1. Многомерные случайные величины и их функции распределения
- •X и y независимые случайные величины.
- •8.2. Вероятность попадания двумерной случайной величины
- •8.3. Числовые характеристики двумерной случайной величины
- •Математическая статистика
- •1. Статистические законы распределения выборки
- •1.1. Вариационный ряд
- •1.2. Полигон и гистограмма
- •1.3. Эмпирическая функция распределения
- •2. Статистические оценки параметров распределения
- •2.1. Точечные оценки
- •2.2. Интервальные оценки
- •2.3. Оценка вероятности появления события через его частоту
- •3. Проверка статистических гипотез.
- •3.1. Статистические гипотезы
- •3.2. Критерии проверки гипотезы
- •3.3. Критерий согласия Пирсона
- •3.4. Критерий согласия Романовского
- •4. Элементы теории корреляции
- •4.1. Статистические зависимости
- •4.2. Линейная регрессия
- •4.3. Корреляционная таблица
- •4.4. Выборочный коэффициент корреляции
- •Литература
- •С о д е р ж а н и е
4. Случайные величины и функции распределения
4.1. Случайные величины
Определение 4.1.
Случайной величиной (СВ) называется
величина Х,
которая в результате опыта может принять
то или иное значение, заранее неизвестно
какое, т.е.
![]() ,
гдее
элементарное событие.
,
гдее
элементарное событие.
Случайные величины бывают двух типов:
1. Дискретные – если возможные значения случайных величин (значе-ния, которые она принимает) могут быть перечислены. Например, число отсутствующих на лекции студентов, количество попаданий в мишень при п выстрелах, число вызовов на АТС и т.д.
2. Непрерывные – если возможные значения случайных величин непре-рывно заполняют некоторый промежуток. Например, время ожидания го-родского транспорта, расстояние от точки попадания до центра мишени, время безотказной работы блока устройства.
Для того, чтобы задать случайную величину, необходимо знать её воз-можные значения и как часто она их принимает, т.е. с какой вероятностью. Для дискретных случайных величин закон распределения обычно зада-ется таблицей следующего вида
|
X |
|
|
… |
|
… |
|
p |
|
|
… |
|
… |
Замечание.
Так как события
![]() образуют полную группу событий, то
образуют полную группу событий, то![]() .
.
Рассмотрим примеры наиболее распространённых дискретных СВ.
1. Биномиальное распределение.
|
X |
0 |
1 |
… |
k |
… |
n |
|
p |
|
|
… |
|
… |
|
2. Распределение Пуассона.
|
X |
0 |
1 |
… |
n |
… |
|
p |
|
|
… |
|
… |
Пример 4.1. Монета брошена три раза. Построить закон распределения случайной величины Х – число появлений герба.
Здесь
![]() .
По формуле Бернулли вычислим
соответст-вующие вероятности:
.
По формуле Бернулли вычислим
соответст-вующие вероятности:
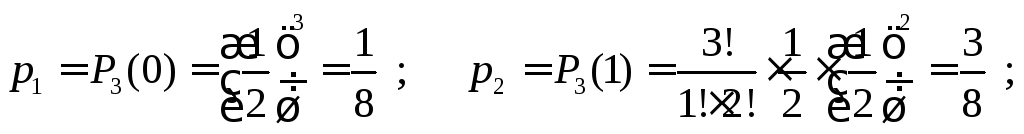
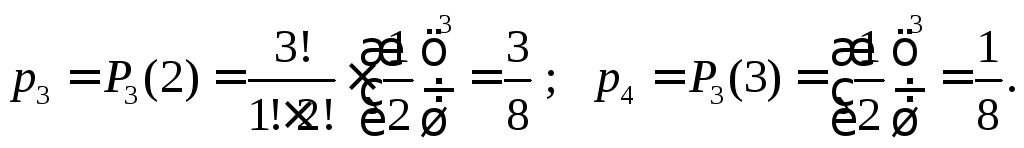
Проверим
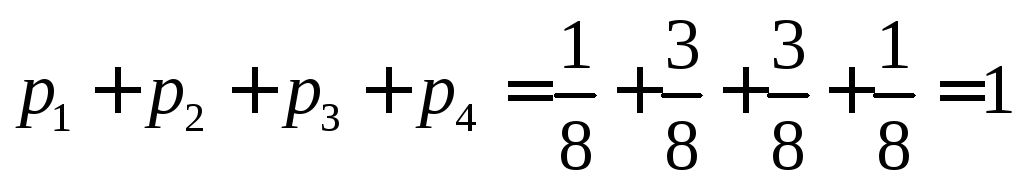 .
.
Получили закон распределения
|
X |
0 |
1 |
2 |
3 |
|
p |
|
|
|
|
4.2. Функция распределения вероятностей для дискретной св
Для количественной
характеристики распределения вероятностей
удобно пользоваться не вероятностью
события
![]() ,
а вероятностью события
,
а вероятностью события![]() .
.
Определение 4.2.
Функция
![]() называется функцией распределения
вероятностей случайной величиныХ
или интегральной
функцией распределения.
называется функцией распределения
вероятностей случайной величиныХ
или интегральной
функцией распределения.
Геометрически это
означает, что
![]()
вероятность того, что случай-ная величина
Х
примет значение, лежащее левее х
на
числовой оси.
вероятность того, что случай-ная величина
Х
примет значение, лежащее левее х
на
числовой оси.
Пример 4.2.
Построить функцию
![]() распределения вероятностей для примера1.
распределения вероятностей для примера1.
1.
![]() ,
для таких значений
,
для таких значений![]() .
.
2.
![]() ,
для таких значений
,
для таких значений .
.
3.
![]() ,
для таких значений
,
для таких значений .
.
4.
![]() ,
для таких значений
,
для таких значений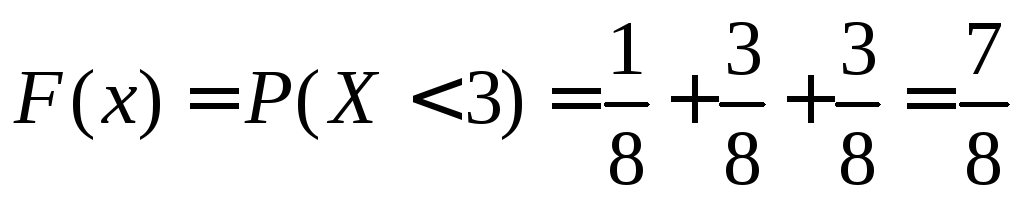 .
.
5 .
.
![]() ,
для таких значений
,
для таких значений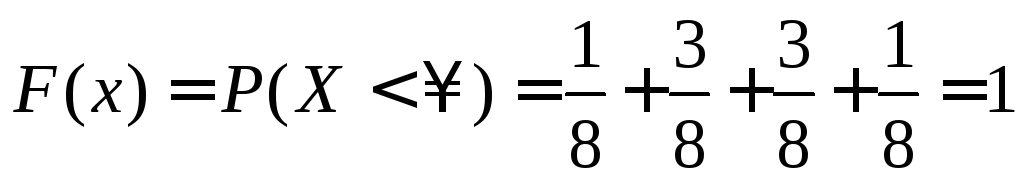 .
.
![]()
1
0,5
0 1 2 3 4 х
Из определения функции распределения следуют её свойства:
1.
![]()
2.
![]()
неубывающая функция.
неубывающая функция.
3.
![]() .
.
4.
Вероятность того, что случайная величина
примет значение, заклю-ченное в интервале
![]() ,
равна
,
равна![]() .
.
Рассмотрим события
![]() ,
тогда
,
тогда![]() ,
так какА
и С
несовместные события. Отсюда
,
так какА
и С
несовместные события. Отсюда
![]() ,
а учитывая, что
,
а учитывая, что![]()
![]() ,
то тогда
,
то тогда![]() .
.
5.
![]() имеет разрывы первого рода во всех
точках, соответству-ющих возможным
значениям СВ, а величина скачка равна
имеет разрывы первого рода во всех
точках, соответству-ющих возможным
значениям СВ, а величина скачка равна
![]() .
.