ІС та технології. Частина 1

141

Послідовність дій така:

1.Вносимо дані, як показано в таблиці нижче, та прописуємо формулу для першої пари значень (затінена комірка).

2.Розмножуємо формулу для всіх інших значень.

3.Увімкнувши режим відображення формул, переконаємося в тому,

що формули переналаштовуються.

4.4.2. Використання абсолютних, відносних та змішаних адрес комірок при побудові формул

З прикладів, розглянутих вище, видно, що формулу, внесену в одну комірку, можна копіювати в інші, і при цьому адреси комірок, що фігурують у цій формулі, автоматично переналаштовуються, тобто адреси автоматично змінюються.

Адреса комірки, яка при копіюванні її у формулах на інші комірки,

змінюється, називається відносною. За умовчанням адреси комірок у формули вносяться як відносні.

На Рис. 4.15 показано, як відносна адреса комірки A1 змінюється відповідно до нової позиції формули.

Рис. 4.15. Переналаштування відносної адреси комірки А1 при копіюванні.

Проте автоматичне переналаштування адрес комірок при копіюванні не завжди потрібне. Часто буває так, що деякі адреси повинні переналаштовуватись, а деякі мають залишатися незмінними.

Адреса комірки, яка при копіюванні її у формулах на інші комірки, не змінюється, називається абсолютною.

143

Рис. 4.18. Переналаштування змішаної адреси комірки A$1 при копіюванні.

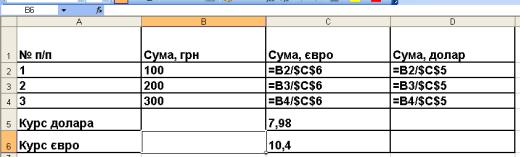
Розглянемо застосування абсолютних та відносних адрес на прикладі задачі. Умова задачі наступна: є суми грошей у гривнях, їх необхідно перевести в євро та доларовий еквівалент, використовуючи запропоновані курси валют.

Оскільки всі формули однотипні, то достатньо побудувати формулу для першого значення, а всі інші отримати розмноженням з допомогою маркера автозаповнення. Формула для розрахунку повинна бути такою, щоб при її розмноженні посилання на комірку, де знаходиться сума в гривнях,

змінювалась, а посилання на комірку, де знаходиться курс валюти,

залишалося незмінним (Рис. 4.19).

Рис. 4.19. Приклад застосування абсолютних та відносних адрес комірок.

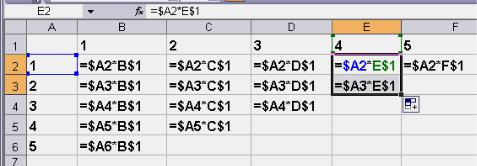
Розглянемо застосування змішаних адрес комірок на прикладі таблиці множення (5х5). Для побудови такої таблиці спочатку потрібно розташувати значення так, як це показано на Рис.4.20. Оскільки всі формули однотипні, то будуємо лише одну - для першої пари значень і далі розмножуємо її.

144

Формулу для розрахунку потрібно побудувати так, щоб при копіюванні формули посилання на перше значення змінювалося в межах стовпця (в

даному випадку це стовпець А), а посилання на друге значення змінювалося в межах рядка (в даному випадку це рядок 1). Правильно побудована формула для першої пари значень та показано, як буде вигляд формули для останньої пари значень показано на Рис.4.20.

Рис. 4.20. Приклад застосування змішаних адрес.

Автоматичні обчислення. Ці обчислення забезпечують швидке формування результатів для даних, що знаходяться в одному стовпці чи в

одному рядку. Обчислення виконуються з допомогою кнопки списку Для виконання обчислень з допомогою функції Автообчислення

необхідно виділити діапазон з даними і обрати із списку потрібну функцію.

Результат з’явиться в наступній після виділеного діапазону комірці.

В Таблиці 4.4 наведено опис команд функції Автообчислення.

145

З цього списку треба виділити окремо функцію додавання. Оскільки ця функція використовується найчастіше, то при натисканні безпосередньо на

саму кнопку , ця дія вибирається автоматично.

4.4.3. Побудова формул з використанням вбудованих функцій

Програма Excel дозволяє використовувати велику кількість вбудованих стандартних функцій для одержання результату з допомогою складних обчислень. Усі функції поділені на кілька категорій для простішого орієнтування.

Програма Мастер функций допомагає на всіх етапах роботи правильно застосовувати функції. Вона дозволяє будувати й обчислювати більшість функцій за два кроки. У програмі впорядкований за алфавітом повний список усіх функцій, в якому можна легко знайти функцію, якщо відомо її ім'я. В іншому разі варто здійснити пошук за категоріями. Функція оперує кількома даними, що називаються її аргументами. Аргумент функції може займати одну комірку чи розміщуватися в групі комірок.

Доступ до стандартних функцій забезпечується викликом Майстра функцій за допомогою:

команди Вставка Функція,

кнопки панелі інструментів Стандартная,

поля імені в рядку формул.

У діалоговому вікні Мастер функций (Рис. 4.21.) необхідно вибрати тип функції в переліку категорія, потім потрібну функцію в переліку Функция та натиснути ОК.

Серед категорій є набір з десяти функцій, використаних останніми, і

набір усіх наявних у програмі функцій (повний алфавітний перелік). Для зручності всі функції згруповані у кілька груп, наприклад, функції дати і часу, математичні, фінансові, статистичні, для роботи з базою даних тощо.

146

Для використання стандартної функції на першому етапі роботи слід виділити ту комірку, в якій повинен з'явитися результат обчислень, потім отримати доступ до Майстра функцій та обрати необхідну функцію.

Рис. 4.21. Вікно програми Мастер функцій.

На другому етапі в діалоговому вікні Майстра функцій слід вказати аргументи функції. Майстер розрізняє аргументи, що повинні враховуватися обов'язково, і аргументи не обов'язкові, але можливі. Щоб задати аргумент функції, потрібно або ввести його адресу з клавіатури, або в таблиці виділити область, де він розташований. Тоді адреса аргументу функції з'явиться у відповідному полі діалогового вікна Майстра функцій. Якщо всі аргументи функції були введені правильно, у діалоговому вікні обраної функції з'являється результат обчислення цієї функції. Він буде розміщений у зазначеній комірці таблиці після натискання кнопки OK. Але після цього комірка продовжуватиме залишатися виділеною, і у рядку формул можна бачити формулу з виглядом обраної функції та її відповідними аргументами.

Для редагування вже існуючої функції слід клацнути мишею на комірці, де знаходиться функція, отримати доступ до Майстра функцій,

відкрити вікно редагування функції (другий етап створення функції). Для того, щоб змінити вміст поля, де знаходяться аргументи, слід безпосередньо внести нові адреси або виділити відповідну групу комірок. Після закінчення редагування натиснути кнопку OK. Можна зробити інакше. Після виділення комірки, де знаходиться функція, у рядку формул з'явиться зміст функції, що

147

містить значення аргументів. Тому редагування можна виконати безпосередньо в цьому рядку. В цьому випадку потрібно встановити курсор у позицію, де зроблена помилка, та виправити.

В Таблиці 4.5 наведені формати та призначення деяких стандартних функцій Excel.

4.4.3.1. Використання функцій одного та декількох аргументів

Розглянемо декілька прикладів побудови формул з використанням

стандартних функцій.

148

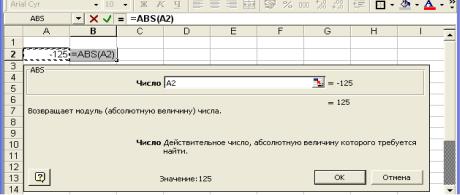
Приклад 1. Визначення модуля числа (використання функції одного аргументу).

Визначити модуль числа можна з допомогою функції ABS з категорії

Математические..

На Рис. 4.22 наведено приклад побудови формули з використанням функції ABS. В якості аргументу функції вказана адреса комірки. Готову формулу можна побачити в рядку формул.

Необхідно звернути увагу на те, що використання Майстра функцій значно спрощує побудову формули.

Рис. 4.22. Приклад використання функції одного аргументу.

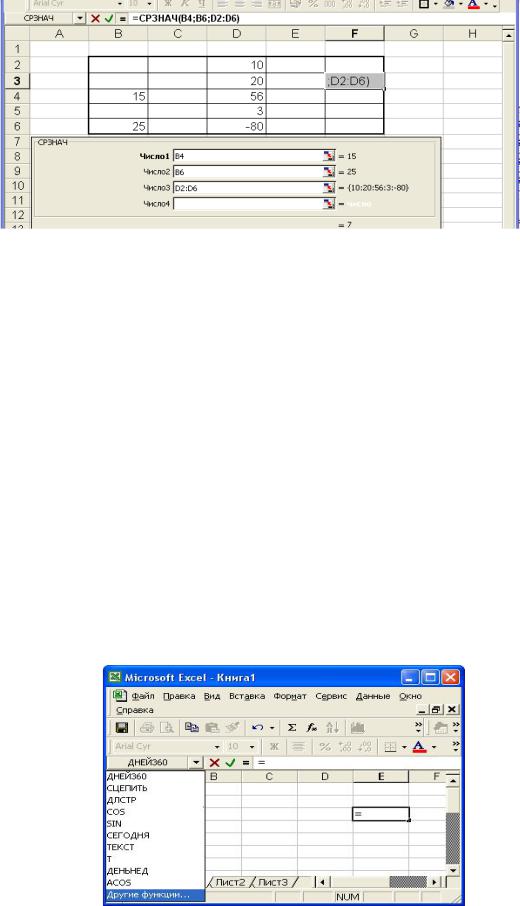
Приклад 2. Визначення середнього арифметичного (використання функції кількох аргументів).

Для розрахунку значення середнього арифметичного можна використати функцію СРЗНАЧ, що належить до категорії Статистические.

На Рис. 4.23 наведено таблицю з вихідними даними та побудову формули з використанням функції СРЗНАЧ з допомогою Майстра функцій.

З введених у відповідне діалогове вікна даних видно, що в полях,

призначених для введення аргументів, вказуються адреси комірок, де безпосередньо знаходяться значення.

Якщо комірки розташовані поруч і утворюють діапазон, то в якості аргументу можна вказувати діапазон. Це показано на прикладі третього аргументу функції.

149

Рис. 4.23. Приклад використання функції кількох аргументів.

4.4.3.2. Використання вкладених функцій

Програма Excel допускає вкладання функцій, тобто параметром однієї функції може бути призначене значення іншої функції.

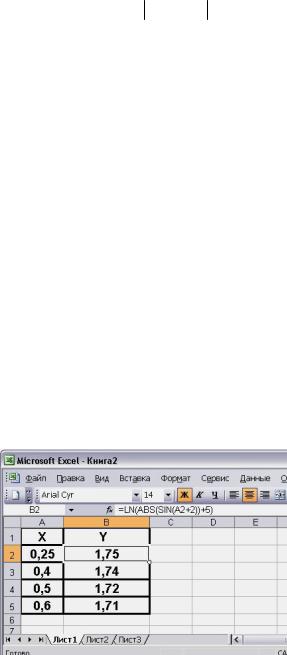
Розглянемо можливість отримання доступу до Майстра функцій з допомогою поля імені у рядку формул. Такий доступ необхідний при роботі з вкладеними функціями.

Список функцій у полі імені стає доступним після того, як в комірці поставлено знак “=” (тобто почали створювати формулу). Розкритий список містить 10 функцій, що використовувалися останнім часом (Рис. 4.24.). Якщо потрібної функції в цьому переліку немає, то доступ до повного списку Майстра функцій можна отримати, обравши пункт Другие фукнции.

Рис. 4.24. Вибір функції з допомогою поля імені у рядку формул.