А) в диметрии; б) на эпюре

Рис. 2.22 Проецирующие плоскости

Плоскости, параллельные плоскостям проекций (дважды проецирующие), называются плоскостями уровня (Рис.2.23а, б, в).

Рис. 2.23. Плоскости уровня

Все точки, лежащие в этих плоскостях, одинаково отстоят от соответствующей плоскости проекций. Любая плоская фигура, расположенная в плоскости уровня, проецируется на параллельную ей плоскость проекций без искажения, т.е. в натуральную величину.

Глава 3. ОТНОСИТЕЛЬНОЕ ПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ, ДВУХ ПЛОСКОСТЕЙ

Прямая относительно плоскости может занимать следующие положения:

• прямая лежит в плоскости (Рис.2.16);

• прямая пересекается с плоскостью;

• прямая параллельна плоскости;

• прямая перпендикулярна к плоскости (частный случай прямой, пересекающейся с плоскостью).

Плоскости могут занимать одна относительно другой следующие положения:

• пересекающиеся плоскости;

• параллельные плоскости;

• взаимно-перпендикулярные плоскости.

3.1. Пересечение прямой общего положения с проецирующей

плоскостью

Если в пространстве прямая общего положения а пересекает горизонтально-проецирующую плоскость Р (Рис.3.1а), то на эпюре (Рис.3.1б) горизонтальная проекция К точки их пересечения будет определяться как точка пересечения горизонтальной проекции Р_н с горизонтальной проекцией а. Фронтальная проекция точки К находится по линии связи на фронтальной проекции прямой а.

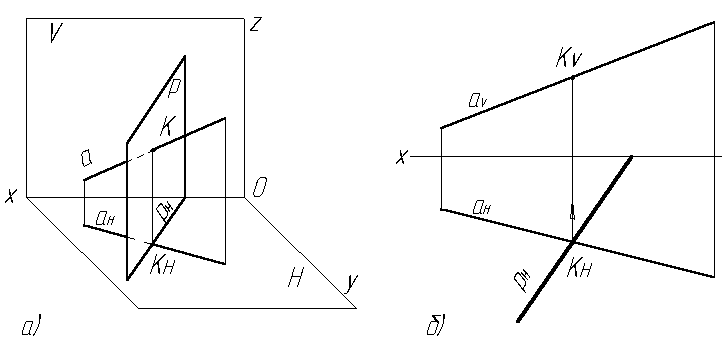
Рис. 3.1. Пересечение прямой с проецирующей плоскостью:

а) в диметрии; б) на эпюре

3.2. Линия пересечения проецирующей плоскости с

плоскостью общего положения

Возьмем горизонтально-проецирующую плоскость Р и плоскость общего положения АВС (рис.3.2а, б). На эпюре (рис.3.2б) плоскость Р проецируется в прямую Р_н. Линия пересечения двух плоскостей d – это линия, принадлежащая каждой из них, а следовательно, и горизонтально-проецирующей плоскости Р. Значит, горизонтальная проекция линии пересечения совпадает с горизонтальной проекцией плоскости d_н = Р_н. Построение фронтальной проекции линии пересечения сводится к построению точек 1_v и 2_v, принадлежащих фронтальным проекциям прямых АС и АВ. Фронтальная проекция d_v линии пересечения d проводится через точки 1_v и 2_v.

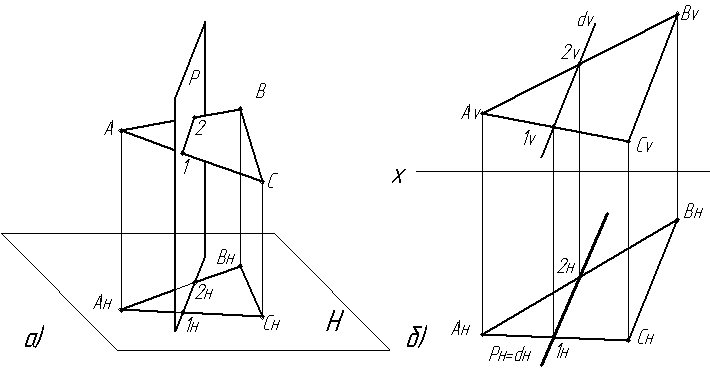
Рис. 3.2. Линия пересечения проецирующей плоскости с плоскостью общего положения: а)- в диметрии; б)- на эпюре

3.3. Пересечение плоскости с прямой общего положения

Чтобы найти точку пересечения прямой общего положения АВ с плоскостью общего положения Q, нужно:

1) через прямую провести вспомогательную плоскость Р (посредник) частного положения;

2) построить линию пересечения (1-2) вспомогательной плоскостиРс заданной;

3) найти точку (I) пересечения заданной прямой с линией пересечения плоскостей (Рис.3.3).

Задача:Найти точку пересечения прямойFEс плоскостью, заданной треугольникомABC(Рис.3.4).

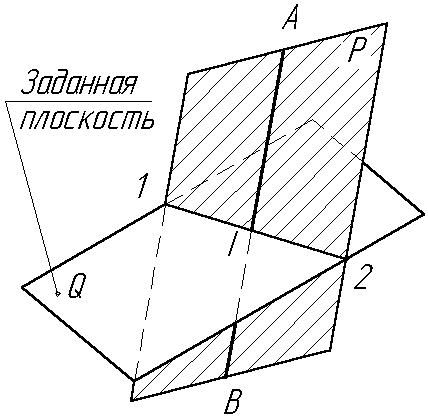
Рис. 3.3. Пересечение прямой линии с плоскостью

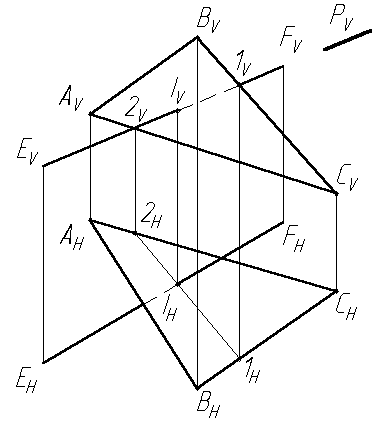
Рис. 3.4. Пресечение прямой линии с плоскостью на эпюре

Решение.

1. Проводим через прямую EF фронтально проецирующую плоскость Р (след Р_v);

2. Находим линию пересечения заданной и вспомогательной плоскостей (1-2);

3. В пересечении горизонтальных проекций прямых FE (F_нE_н) и 1-2 (1_н 2_н) находим горизонтальную проекцию точки пересечения прямой с плоскостью (I_н). Точка I_v строится по линии связи.

Видимость прямой и плоскости определяется по конкурирующим точкам (Рис.2.10а, б).