Способом плоскопараллельного перемещения

4.2.3. Способ вращения вокруг линии уровня

Этот способ удобно применять в тех случаях, когда требуется расположить плоскую фигуру параллельно плоскости проекций, что достигается за один поворот.

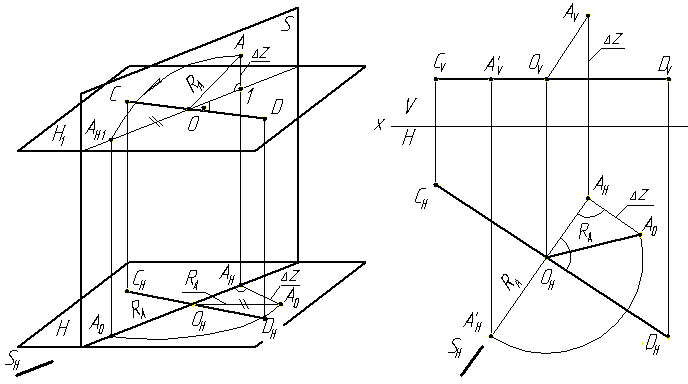
Рассмотрим сущность способа на примере поворота точки А вокруг горизонтали (Рис.4.13а).

Возьмем в пространстве точку А и горизонталь СД и повернем точку А вокруг СД до положения, когда она окажется в горизонтальной плоскости Н₁, проходящей через СД. Траекторией точки А будет окружность R=ОА, центр О которой лежит на прямой СД. Плоскость окружности, то есть плоскость S вращения точки А перпендикулярна к прямой СД – оси вращения, а следовательно и к плоскости Н. Поэтому горизонтальная проекция А будет перемещаться по горизонтальному следу S_Н плоскости вращения, перпендикулярному к горизонтальной проекции С_НД_Н оси вращения.

Чтобы выполнить такой поворот точки А на чертеже, (Рис 4.13б), необходимо соблюдать следующие требования:

1.Провести через точку А_Н прямую (след S_Н плоскости вращения), перпендикулярную к С_НD_Н оси вращения, их пересечение определяет положение центра вращения О точки А и, следовательно, проекции радиуса вращения О_НА_Н и О_VA_V.

2.Определить одним их известных способов натуральную величину радиуса R_A (О_НА_О). (На рис. 4.13б применен способ построения прямоугольного треугольника О_НА_НА_О).

A) б)

Рис.4.13 Определение расстояния от точки А до линии СD способом вращения вокруг линии уровня

3.Отложить от центра О_Н на прямой, перпендикулярной к С_НD_Н, отрезок О_НА_О, равный натуральной величине радиуса R_A.

Задача: Определить натуральную величину треугольника АВС способом вращения вокруг горизонтали (Рис. 14).

Решение. Если за ось вращения построить горизонталь, принадлежащую плоскости треугольника АВС, то для поворота этой фигуры в положение, параллельное горизонтальной плоскости проекций, достаточно повернуть всего одну точку треугольника, не лежащую на оси вращения, а именно точку В. Остальные точки строятся из условия принадлежности их плоскости фигуры. Горизонталь А1 проведена через вершину А треугольника до пересечения с продолжением стороны ВС в точке 1. В треугольнике АВ1 вершины А и 1 лежат на оси вращения и не изменят своего положения при вращении вокруг горизонтали. Вращая точку В способом, рассмотренным на рис.4.13б, определяют положение ее новой проекции В¹. Соединив ее с точками А и 1, получим треугольник АВ’1, повернутый в положение, параллельное плоскости Н. Положение проекции точки С’, вершины С находят, проведя через точку С прямую перпендикулярную к оси вращения А1 до пересечения со стороной В1, поскольку все точки треугольника при его повороте перемещаются в параллельных плоскостях. Проекция А_НВ’_НС’_Н треугольника АВС определяет его натуральную величину, т.к. А_VВ’_VС’_V параллельна Н.

Глава 5. Многогранники

5.1. Общие положения

Многогранником называют геометрическое тело, ограниченное плоскими многоугольниками. Эти многоугольники называют гранями общие стороны смежных многоугольников – ребрами, вершины многогранных углов, образованных его гранями, сходящимися в одной точке - вершинами многогранника.

Совокупность вершин и соединяющих их ребер называют сеткой многогранника.

Рассмотрим только выпуклые многогранники, то есть такие, все грани которых лежат по одну сторону от каждой его грани.

Из всех многогранников наибольший практический интерес представляют призмы, пирамиды и правильные многогранники.

Многогранник, две грани которого n–угольники, лежащие в параллельных плоскостях, а остальные грани параллелограммы, называется n–угольной призмой.

Призма, боковые ребра которой перпендикулярны плоскостям оснований, называется прямой призмой.

Если боковые ребра призмы не перпендикулярны плоскостям оснований, то она называется наклонной призмой.

Многогранник, одна из граней которого произвольный многоугольник, а остальные грани треугольники имеющие общую вершину, называется пирамидой (рис.5.1б).

Если основание пирамиды правильный многоугольник и вершина пирамиды лежит на перпендикуляре восстановленном из центра этого многоугольника, то она называется правильной пирамидой (рис.5.1б).

К правильным многогранникам относятся те, грани которых представляют собой равные и правильные многоугольники, например: гексаэдр (куб) – правильный шестигранник (рис.5.1а), тетраэдр – правильная треугольная пирамида (рис.5.1в), октаэдр – правильный восьмигранник, додекаэдр – правильный двенадцатигранник, икосаэдр – правильный двадцатигранник.

Правильный четырехгранник, или тетраэдр (рис.5.1в), состоит из четырех равносторонних и равных треугольников. Они соединены по три около каждой вершины. Тетраэдр представляет собой частный случай пирамиды. Правильный шестигранник (куб), или гексаэдр, состоит из шести равных квадратов, соединенных по три у каждой вершины.

На комплексном чертеже построение многогранников сводится к построению его сетки (проекций его вершин и ребер). Из многогранников наибольший практический интерес представляют призмы, пирамиды и правильные многогранники.

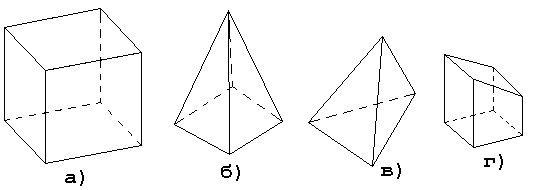
Рис. 5.1 – Многогранники: а) куб; б) пирамида; в) тетраэдр;