6.2. Пространственные кривые

Кривую, точки которой не лежат в одной плоскости, называют пространственной или линией двоякой кривизны.

Пространственные кривые так же, как и плоские, могут быть закономерными или общего вида. К закономерным относятся винтовые линии (гелисы), которые широко применяются в технике, являясь определяющими поверхностей резьбы, червяков, пружин и т.п. Название винтовой линии определяется видом поверхности, по которой движется точка, образующая гелису.

Цилиндрическая винтовая линия.

Цилиндрическая винтовая линия представляет собой траекторию точки, равномерно движущейся по образующей цилиндра, которая, в свою очередь, равномерно вращается вокруг оси цилиндра.

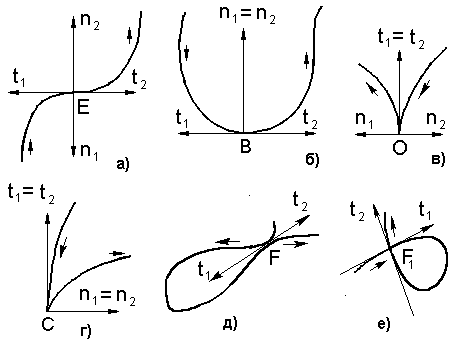
Рис. 6.4. Особые точки на линии

Основными параметрами этой кривой являются: диаметр окружности цилиндра, шаг р винтовой линии, направление винтовой линии и угол подъема . Шагом р называется расстояние, пройденное точкой по образующей цилиндра за один полный оборот по окружности. Шаг может быть постоянным и переменным. Если винтовая линия поднимается по видимой стороне цилиндра слева на право, то она правая. Угол подъема винтовой линии выражается формулой:

tg= р/d

где: р – шаг винтовой линии;

d – диаметр основания цилиндра.

Для построения проекций винтовой цилиндрической линии шаг (высота цилиндра) и окружность основания делятся на одинаковое число (n) равных частей. На рисунке 6.5 n=12.

При перемещении на 1/12 часть по окружности точка переместится на (1/12)р (шага) по образующей цилиндра. Таким образом, фронтальные проекции точек гелисы получаются при пересечении горизонтальных прямых деления шага с линиями проекционной связи, проведенными из соответствующих точек деления окружности (см. рис.6.5). Так как ось цилиндра является горизонтально-проецирующей прямой, то горизонтальная проекция гелисы совпадает с окружностью основания цилиндра. Фронтальная проекция цилиндрической винтовой линии - синусоида.

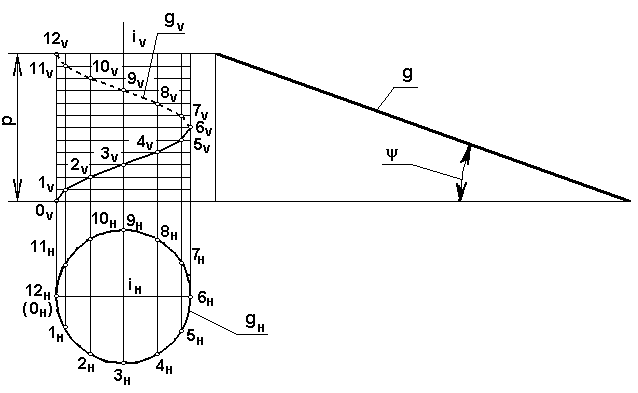
Рис. 6.5. Цилиндрическая винтовая линия и ее развертка

Разверткой гелисы является гипотенуза прямоугольного треугольника, один из катетов которого равен шагу р , а второй – длине окружности основания цилиндра d. Из этого треугольника определяется и угол .

Винтовая линия является линией кратчайших расстояний между двумя точками на поверхности цилиндра.

Глава 7. Кривые поверхности

7.1. Общие сведения

Поверхность можно представить и как след, оставляемый линией при ее непрерывном движении в пространстве. Линию, которая перемещается в пространстве, называют образующей поверхности, а линии, которые определяют движение образующей – направляющими поверхности. Способ образования поверхности движением линии называется кинематическим, а поверхности, полученные этим способом – также кинематическими.

Кинематический способ позволяет задать поверхность на чертеже минимальным числом линий и точек.

Определитель поверхности должен включать условия, позволяющие задать данную поверхность на чертеже. Некоторые из параметров определителя могут быть заданы графически (вид и положение образующих или направляющих поверхности) или аналитически (величина радиуса сферы, угол наклона образующей конуса к его оси и т.п.), но кроме этих параметров необходимо задать еще способ (алгоритм) построения на чертеже точек и линий, принадлежащих поверхности.

Таким образом, каждый определитель поверхности включает в себя графоаналитическую и алгоритмическую характеристику поверхности. Одна и та же поверхность может быть образована по различным законам, т.е. иметь несколько различных определителей.

Определитель поверхности: l,iA₁

Где l,i– графическая часть определителя;

A₁ – алгоритм (закон) образования поверхности.

Образующая поверхности может быть прямой и кривой линиями, постоянной и переменной.

По виду образующей, поверхности делятся на линейчатые (прямо линейчатые) и не линейчатые (криво линейчатые).

Направляющих может быть несколько или одна. Любая линейчатая поверхность должна иметь три направляющие. У кривых поверхностей направляющими являются также кривые.

Поверхности разделяются на развертывающиеся и не развертывающиеся. Развертывающиеся поверхности могут быть совмещены с плоскостью без разрывов и складок. Их смежные образующие должны быть параллельными или пересекающимися прямыми. У не развертывающихся поверхностей смежные образующие должны быть скрещивающиеся прямые или кривые. Все не линейчатые поверхности – не развертывающиеся.