Г) призма усеченная
На рисунке 5.2 представлен комплексный чертеж прямой треугольной усеченной призмы. При построении проекций точек, лежащих на гранях призмы, необходимо выполнять условие принадлежности точки плоскости. Если задана фронтальная проекция точки К(КV), то горизонтальная ее проекция (КН) будет лежать на следе проецирующей грани ВССВ.
Рис. 5.2. Построение проекций точки К принадлежащей
Грани вcc’в’
Рассмотрим комплексный чертеж треугольной призмы, ребра которой произвольно наклонены к плоскостям проекций Н и V (рис. 5.3).
Рис. 5.3. Построение проекций точки К принадлежащей
Грани авв’а’
Требуется построить горизонтальную проекцию (КН) точки К по известной ее фронтальной проекции (КV), при условии, что точка К принадлежит грани АВВА. Выбираем в грани АВВА любую из прямых, проходящую через данную точку К. Такой прямой может быть прямая 12 произвольного положения, пересекающая ребра АА и ВВ или прямая (КЗ), параллельная боковым ребрам и пересекающая ребро АВ в точке 3. Фронтальные проекции (1V2V) и (КVЗV) прямых 12 и КЗ проходят через фронтальную проекцию (КV) искомой точки. Горизонтальные проекции (1Н2Н) и (КНЗН) определяются по условию принадлежности прямых данной грани АВВА. На пересечении линии связи с горизонтальной проекцией одной из вспомогательных прямых и будет горизонтальная проекция КН точки К.
На комплексном чертеже треугольной пирамиды SАВС рисунок 5.4 требуется построить фронтальную проекцию (КV) точки К, принадлежащей грани SBC по заданной ее горизонтальной проекции КН. Ход построения при помощи вспомогательных прямых линий (первый вариант с помощью прямой S2, второй вариант с помощью прямой К1//ВС) показан на чертеже стрелками.
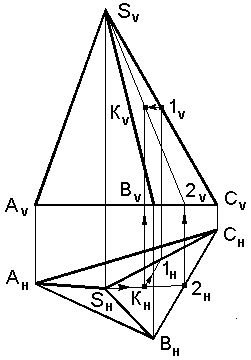
Рис. 5.4. Построение проекций точки К принадлежащей
Грани sвс
5.2. Пересечение многогранников плоскостью
Линией пересечения многогранника плоскостью в общем случае будет плоский многоугольник. Такой многоугольник может быть построен или по точкам пересечения с секущей плоскостью ребер многогранника или по линиям пересечения граней многогранника с плоскостью, т.е. задача сводится к определению точек пересечения прямой с плоскостью или к определению линий пересечения плоскостей.
Плоскую фигуру, полученную от пересечения многогранника плоскостью, называют сечением. Многоугольник сечения может вырождаться в прямые линии и точки. Число сторон многоугольника сечения равно числу граней многогранника, пересекаемых секущей плоскостью.
В зависимости от направления и положения секущей плоскости сечением куба может быть: треугольник, четырехугольник, пятиугольник и шестиугольник, как это показано на рисунке 5.5.
Если секущая плоскость будет параллельна плоскости проекций, то фигура сечения проецируется на эту плоскость проекций без искажения – в натуральную величину.
Рис. 5.5. Возможные сечения призмы
Во всех других случаях натуральный вид сечения определяется любым из способов, которые позволяют определить натуральную величину плоской фигуры.
Задача: Построить проекции и натуральную величину сечения пирамиды SABCD, пересеченной фронтально-проецирующей плоскостью Q (рис.5.6).
Рис. 5.6. Построение многоугольника сечения и определение его натуральной величины
Решение:
Здесь многоугольник сечения определяется по точкам пересечения ребер пирамиды с плоскостью Q.
Фронтальная проекция сечения (1V2V3V4V) вырождается в прямую линию, совпадающую со следом QV проецирующей плоскости Q. Горизонтальные проекции вершин многоугольника сечения находятся по их известным фронтальным проекциям на пересечении линий связи с соответствующими проекциями ребер пирамиды.
Фигурой сечения является многоугольник 1234, натуральная величина которого определена способом плоскопараллельного перемещения.
Если многогранник пересекается плоскостью общего положения, то для определения линии пересечения необходимо воспользоваться известными способами преобразования ортогональных проекций.
Задача: Построить проекции и натуральную величину сечения прямой треугольной призмы, стоящей на плоскости Н, плоскостью общего положения, заданной линией ската s и горизонталью h (рис.5.7).
Рис. 5.7. Построение сечения призмы плоскостью общего