3.8. Взаимно перпендикулярные плоскости
Если плоскость проходит через перпендикуляр к другой плоскости, то плоскости взаимно - перпендикулярны.
Задача: Через точку К провести одну из возможных плоскостей, перпендикулярных к заданной плоскости.
Решение.
Возможны два варианта:
Первый вариант решения. Через точку К провести прямую, перпендикулярную заданной плоскости, и через нее провести любую плоскость (Рис. 3.12);
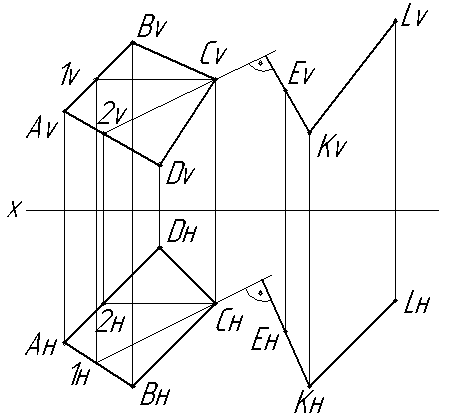
Рис 3.12 Взаимно перпендикулярные плоскости
Второй вариант решения. Через точку К провести плоскость, перпендикулярную одной из сторон параллелограмма, например, ВС, задав ее горизонталью и фронталью (рис.3.13).
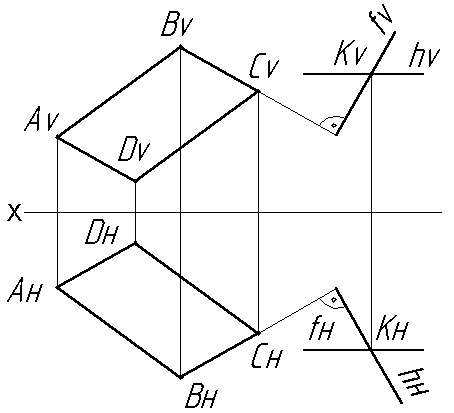
Рис. 3.13. Плоскость, заданная прямыми hиf, перпендикулярная плоскостиABCDи линииBC
Глава 4. Способы преобразования чертежа
Решение позиционных и метрических задач значительно упрощается при преобразовании чертежа так, чтобы заданные геометрические объекты оказались в наиболее удобном – частном положении относительно плоскостей проекций. Это достигается либо способом замены плоскостей проекций, либо способом вращения.
4.1. Способ замены плоскостей проекций
Сущность этого способа заключается в том, что рассматриваемый геометрический объект не изменяет своего положения в пространстве, а заменяется одна из плоскостей проекций, при этом соблюдаются следующие условия: новая плоскость должна быть перпендикулярна к оставшейся (незаменяемой) плоскости проекций; положение новой плоскости (новой оси) выбирается в зависимости от условий задачи; линии связи в новой системе проекции перпендикулярны новой оси; расстояния новых проекций от новой оси равны расстояниям от заменяемых проекций до старой оси.
Преобразование чертежа точки и прямой
Рассмотрим сущность преобразования чертежа способом замены плоскостей проекций на примере чертежа точки. Пусть в системе плоскостей проекций V/Hзадана точкаАна (рис.4.1).
Рис. 4.1. Преобразование чертежа точки в диметрии
Рис 4.2. Преобразование чертежа точки на эпюре
Заменим плоскость VнаV1перпендикулярную к плоскостиНи под некоторым произвольным углом к плоскостиV. Горизонтальная плоскость проекций не меняет своего положения, т.е. осуществляется переход от системыX ( V/H )к новойX1 (V1/H). Плоскость V1пересекается с плоскостьюHпо прямойХ1, которая определяет новую ось проекций. ПроекцияAHостается без изменений, так как точкаАи плоскостьНне меняли своего положения в пространстве. Для нахождения новой фронтальной проекции точкиAV1, достаточно спроецировать ортогонально точкуАна плоскостьV1. На рис.4.1 видно, что расстояние новой фронтальной проекцииAV1точкиАот новой осиХ1равно расстоянию от старой фронтальной проекцииAVдо старой осиХ:|AV AХ| = |AV1 AХ1| .
На рис.4.2 осуществлено совмещение плоскости V1сHвращением относительно осиX1.
Задача: Преобразовать горизонталь АВ во фронтально проецирующую прямую. (рис.4.3).
Рис 4.3. Преобразование чертежа прямой
Решение. Новая плоскость V1 перпендикулярна плоскости H и АНВН. Расстояния от точек АV1 и ВV1 до новой оси Х1 на плоскости V1 равно расстоянию от точек АV и ВV до старой оси Х.
Задача: Определить натуральную величину и угол наклона отрезка АВ прямой общего положения к плоскости H и V. (рис.4.4а, б).
