Глава 1. Метод проецирования

1.1. Центральная проекция

Выберем в пространстве плоскость проекций, которую обозначим буквой Р. Выберем также точку S, не лежащую в плоскости Р, и назовем ее центром проекций (Рис.1.1).

Рис. 1.1. Центральная проекция точек

Плоскость Р и точка S составляют аппарат центрального проецирования. Проецирование проводится следующим образом: если дана произвольная точка А пространства, то для построения ее проекции на плоскость Р проводится прямая SA и находится точка пересечения А_р прямой SA с плоскостью Р. Точка А_р является центральной проекцией точки А на плоскость Р.

Прямая SA называется проецирующей.

Для построения проекций нескольких точек следует через взятые точки и центр проекций провести проецирующие прямые до пересечения их с плоскостью Р. Полученные точки и будут являться центральными проекциями соответствующих точек А, В, С.

При заданном центре и плоскости проекций данная точка имеет единственную проекцию, так как проецирующая прямая может пересечься с плоскостью проекций только в одной точке. Одна проекция точки не определяет ее положения в пространстве, т. к. на проецирующей прямой, например, SD_Pможет лежать множество точек, как-то точкиD₁иD₂(Рис.1.1).

1.2. Параллельная проекция

Если центр проекций удалить в бесконечность, то проецирующие прямые станут параллельны между собой. Вместо центра проекций задается направление проецирования S (см. рис.1.2) и плоскость проекций Р. Проекции точек А, В и т.д. можно получить, если провести проецирующие прямые АА_р, ВВ_р и т.д., параллельно S.

Рис. 1.2. Параллельная проекция точек

А_р, В_р, С_р – проекции соответствующих точек.

В зависимости от направления проецирования параллельные проекции делятся на прямоугольные (SP) и косоугольные (S не Р).

1.2.1. Свойства параллельных проекций

Проекция прямой линии есть прямая линия (Рис.1.3). Плоскость, определяемая двумя пересекающимися прямыми АВ и АА_р, пересекает плоскость проекций Р по прямой А_рВ_р.

Исключение составляет проекция прямой линии, которая параллельна направлению проецирования. Такая прямая проецируется в точку (Рис.1.3).

Следствия из свойства.

Если точка лежит на прямой, то ее проекции лежат на соответствующих проекциях прямой (Рис.1.3).

Если две прямые пересекаются, т.е. проходят через одну точку Е, то и соответствующие проекции этих прямых пересекаются, проходят через проекции точек пересечения Е_р (Рис.1.4).

Если прямые АВ и СD параллельны, то и соответствующие их проекции параллельны, т.е. А_рВ_р  C_pD_p (Рис.1.5).

Отношение отрезков параллельных прямых равно отношению их проекций:(Рис.1.6).

Отношение отрезков прямой равно отношению их проекций (Рис.1.7).

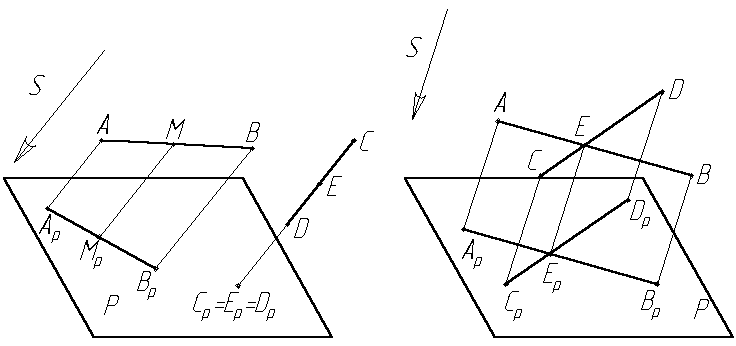
Рис. 1.3. Проекции прямых линий Рис. 1.4. Проекции пересе-

кающихся прямых

Рис. 1.5. Проекции параллельных Рис. 1.6. Проецирование

прямых отрезков прямой

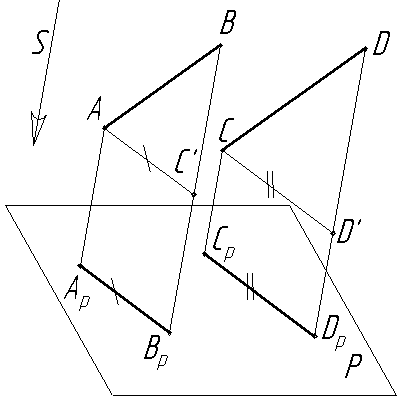
Рис. 1.7. Проекции отрезков параллельных прямых

1.3. Показатели искажения

Отношение длины проекции отрезка к длине самого отрезка называется показателем искажения К отрезка (Рис.1.6), величина которого определяется из следующего соотношения:

При косоугольном проецировании длина проекции может быть равна, больше или меньше длины самого отрезка. Показатель искажения может быть равен, больше или меньше единицы, т.е. 0 ≤ К ≤  (Рис.1.8).

Если отрезок BD параллелен плоскости проекций Р – он проецируется без искажения К=1. Если отрезок EF параллелен направлению проецирования S, он проецируется в точку К=0. Если величина угла между направлениями проецирования и плоскостью проекций близка к нулю, то длина проекции отрезка приближается к бесконечности К  .

При прямоугольном проецировании длина проекции отрезка может быть равна или меньше длины самого отрезка. Показатель искажения может быть равен или меньше единицы 0 ≤ К≤ 1 (Рис.1.9).

Из рассмотренных ранее рисунков (Рис.1.1 – Рис.1.9) видно, что при заданном направлении проецирования и плоскости проекций данная точка или система точек имеют единственную проекцию. Задав

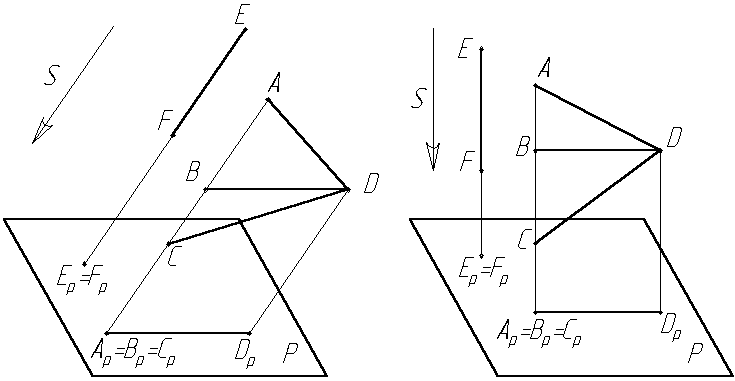
Рис. 1.8. Коэффициент искажения Рис. 1.9. Коэффициент искаже-

при косоугольном проецировании ния при прямоугольном

проецировании

плоскость проекций и направление проецирования можно получить изображение пространственной формы на плоскости проекций. Однако на одной проекции не выполняется требование обратимости, предъявляемое к чертежу, т.е. по одному изображению не возможно воспроизвести заданную форму в пространстве. Возникает необходимость изучения в курсе начертательной геометрии способов построения обратимых чертежей. Наиболее распространенным способом построения обратимых чертежей является прямоугольное проецирование на 2…3 взаимно перпендикулярные плоскости.